高斯-约旦消元法

高斯-约旦消元法

此算法是基于高斯消元的基础上改进而成的，唯一不同之处是多进行了几次矩阵变换使得化为行最简型矩阵。相比于高斯消元法此方法效率较低，但是不需要回带求解

此算法的过程大概为：首先确定每个$a[i][i]$不为$0$（如果为$0$就和下面的行替换），接着将每个$a[i][i]$通过行变换化为$1$（该行都除以$a[i][i]$），然后通过行变换将每列除了$a[i][i]$以外的都消成$0$，重复$n$次即可

如下是一个求解过程的示例：

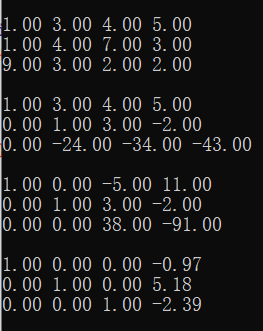
首先最简单的操作是输入增广矩阵:

scanf("%d",&n);
for(int i=1;i<=n;i++)
  for(int j=1;j<=n+1;j++)
  scanf("%lf",&a[i][j]);

接下来开始消元的第一步：判断是否有解

我们每次考虑$a[i][i]$，先看该列的元素是否全为$0$。第二次以后时我们都没有考虑该列上面得到元素，因为他们已经可以被化简为$0$。

for(int i=1;i<=n;i++){
     
	tmp=i;
    // 一直找第i列第tmp行的首个非零元素
	while(fabs(a[tmp][i])<esp && tmp<=n) tmp++;
	if(tmp==n+1) return false;  //如果n行的第i列全判断过仍然没有找到，说明无解
}

消元的第二步：找到该列第一个非零元素后将该行和第$i$行元素作行交换

我们上面判断是否有解实际上是在找第$i$列第一个非零元素

//将第tmp行第i列元素不为0的那一行与当前第i行交换
for(int j=1;j<=n+1;j++)
	swap(a[i][j],a[tmp][j]);

消元的第三步：将第$i$行第$i$列的元素化为$1$

方法是当前行的所有元素都除以$a[i][i]$

double p=a[i][i];
for(int j=1;j<=n+1;j++)
	a[i][j]=a[i][j]/p;

消元的第四步：将第$i$列除了第$i$行的元素全消成$0$

方法是第$j$行每个元素$a[j][k]$都减去$a[j][k]\ast a[i][k]$

for(int j=1;j<=n;j++){
     
	if(i!=j){
     
		double t=a[j][i];
		for(int k=1;k<=n+1;k++)
			a[j][k]-=t*a[i][k];
	}
}

其实上面四步写在一个$for$循环即可，因此得到该函数：

const double esp=1e-8;
double a[1005][1005];

bool gauss(int n){
     
    int tmp;
    for(int i=1;i<=n;i++){
     
        tmp=i;
        while(fabs(a[tmp][i])<esp && tmp<=n)
        tmp++;
        if(tmp==n+1) return false;
        for(int j=1;j<=n+1;j++)          
            swap(a[i][j],a[tmp][j]);
        double p=a[i][i];                
        for(int j=1;j<=n+1;j++)
            a[i][j]=a[i][j]/p;         
        for(int j=1;j<=n;j++){
     
            if(i!=j){
     
                double q=a[j][i];
                for(int k=1;k<=n+1;k++)
                a[j][k]-=q*a[i][k];
            }
        }
    }
    return true;
}

如果有多个解的情况呢？如果某变量有多个解，那么该行的$n+1$个数一定都等于0

因为每次我们都先保证前面的$a[i][i]$都一定要为$1$，因此一定在最后几个$a[i][i]$。看题目要求我们将通解设置为某些常量，而且还需要注意上面有不会完全消为$0$的项，那么我们就需要代入通解求解。

下面是存在一个通解并且将其设置为1的例子：

void solve(){
     
    if(fabs(a[col][col])>esp){
           //有唯一解
        for(int i=1;i<=col;i++) x[i]=fabs(a[i][col+1]);
        return;
    }
    //否则肯定最后一个是不定解，由于求最小的整数解那么即为1
    x[col]=1;
    for(int i=1;i<col;i++){
     
        x[i]=fabs(a[i][col]);
    }
}

bool gauss(int n){
     
    int tmp;
    for(int i=1;i<=n;i++){
     
        print();
        tmp=i;
        while(a[tmp][i]==0 && tmp<=n) tmp++;
        if(tmp==n+1) return false;
        for(int j=1;j<=n+1;j++)
            swap(a[i][j],a[tmp][j]);
        double p=a[i][i];
        for(int j=1;j<=n+1;j++)
            a[i][j]=a[i][j]/p;
        for(int j=1;j<=n;j++){
     
            if(i!=j){
     
                double q=a[j][i];
                for(int k=1;k<=n+1;k++)
                a[j][k]-=q*a[i][k];
            }
        }
    }
    solve();
    return true;
}