3.MATLAB实现有限脉冲响应数字滤波器（FIR）

本文是FIR数字滤波器设计，如果需要了解模拟滤波器或者IIR的内容，可以看我写的另外两篇博客，如下：

1.巴特沃斯模拟滤波器（低通，高通，带通，带阻）设计-MATLAB实现

2.MATLAB实现无限脉冲响应数字滤波器（IIR）

前言

• IIR数字滤波器主要是模仿模拟滤波器的设计方法，所以在设计中只考虑了幅度特性，没有考虑相位特性，设计出来的滤波器一般是非线性的。
• 有限脉冲响应（FIR）滤波器在保证幅度特性满足要求的情况下，很容易做到线性相位特性。

1. 函数介绍

hn=fir1(M,wc,'ftype',window)

M - 滤波器阶数，如果窗口长度为N，那么M就是N-1
wc - 6dB截止频率，wc = (wp + ws) / 2;
ftype: 滤波器类类型

• 当输入wc为一维向量时：
  设计的低通滤波器的话ftype不需要填，设计高通滤波器的话令’ftype’=’high’

• 当输入wc为二维向量[wcl,wcu]时：
  设计的带通滤波器的话ftype不需要填，设计带阻滤波器的话令’ftype’=’stop’

window - 窗口类型，包括下面这些类型

• boxcar(N) - 矩形窗
• bartlett(N) - 三角形窗
• hanning(N) - 汉宁窗
• hamming(N) - 哈明窗
• blackman(N) - 布莱克曼窗
• kaiser(N,beta) - 凯赛窗

2. 设计方法

以低通滤波器设计为例

例： 设计线性低通滤波器，通带频率wp = pi / 4 rad, 阻带频率 ws = pi / 2；通带衰减1dB,阻带衰减40dB。

（1）选择窗口类型

各种类型窗口的具体参数如下：

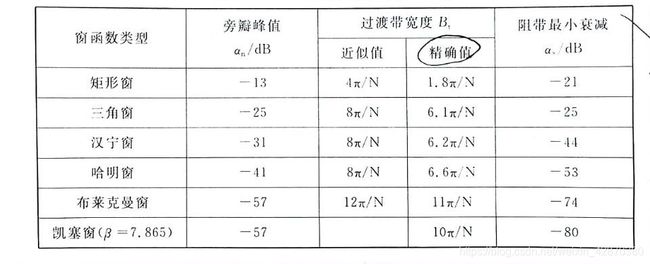
本题中阻带最小衰减40dB，而汉宁窗最小衰减达到了44dB，所以选择汉宁窗

（2）首先计算窗口长度N

本题中，过渡带带宽为 $B_t=w_s-w_p=0.25\pi$

$$N\ge \frac{6.2\pi }{B_t}=\frac{6.2\pi }{0.25\pi }=24.8$$

这里我们向上取整，取窗口长度 N=25

（3）求截止频率

截止频率
$$w_c=\frac{w_p+w_s}{2}=0.375\pi (rad)$$
对 $\pi$ 归一化后得 $wc=0.375$

（4）调用fir1计算

计算函数如下：

hn=fir1(N-1,wc,hanning(N))

（5）滤波

调用filter函数，如下：

y=filter(hn,1,x);

这里hn是刚设计好的滤波器，x是输入信号，y就是滤波后的信号。

2. 低通数字滤波器设计

例： 设计线性低通滤波器，通带频率wp = pi / 4 rad, 阻带频率 ws = pi / 2；通带衰减1dB,阻带衰减40dB。

计算流程刚已经讲过了，直接上代码

%低通滤波器
 
wp=pi/4;ws=pi/2;
DB=ws-wp;           %计算过渡带宽度
N=ceil(6.2*pi/DB); %根据表7.2.2汉宁窗计算所需h(n)长度N0
 
wc=(wp+ws)/2/pi;    %计算低通滤波器截止频率(关于π归一化）
hn=fir1(N-1,wc,hanning(N));  %调用fir1计算低通滤波器参数

至此，FIR数字低通滤波器设计完成了，如果有输入噪声信号x的话，调用y = filter(hn,1,x)，得到的y就是滤波后的信号了。

接着我们画出数字低通滤波器的幅频特性曲线，代码如下：

%以下是绘图部分
%计算hn的1024点fft，即求其幅频特性
M=1024;
hk=fft(hn,M);
 
%1024点对应2pi，512点对应pi，我们在1-pi之间取点，求出该点的幅度
k=1:M/2;
fd = abs(hk(k));
 
%横坐标对pi归一化一下，表示起来更清楚，对pi归一化就是0-511 对 M/2归一化
w=(0:M/2-1)/(M/2);
 
figure;
plot(w,20*log10(fd));
axis([0,1,-80,5]);
xlabel('ω/π');ylabel('20lg|Hg(ω)|');
grid on

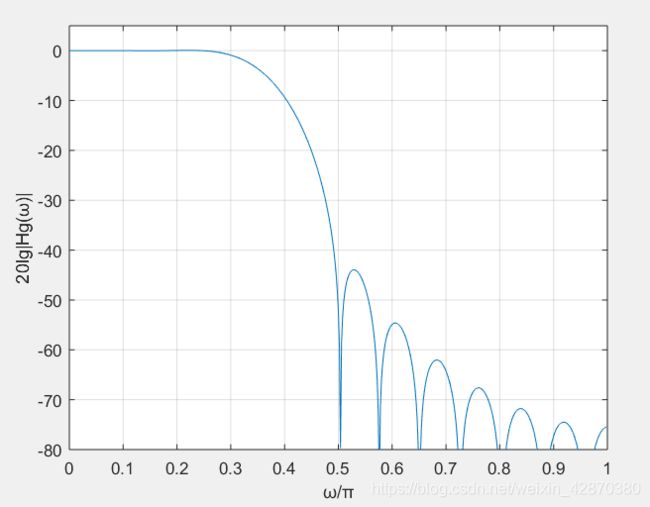
结果如下：

3. 高通数字滤波器设计

高通滤波器与低通滤波器设计方法类似，不过要注意，设计高通和带阻FIR滤波器时，窗口长度N必须为奇数。

例： 设计线性高通滤波器，通带频率wp = pi / 2 rad, 阻带频率 ws = pi / 4；通带衰减1dB,阻带衰减40dB。

代码如下：

%高通滤波器
 
wp=pi/2;ws=pi/4;
DB=wp-ws;           %计算过渡带宽度
N0=ceil(6.2*pi/DB); %计算所需h(n)长度N0

N = N0 + mod(N0+1,2); %保证N为奇数

wc=(wp+ws)/2/pi;    %计算高通滤波器截止频率(关于π归一化）
hn=fir1(N-1,wc,'high',hanning(N));  %调用fir1计算高通滤波器参数

至此，FIR数字高通滤波器设计完成了

如果有输入噪声信号x的话，调用y = filter(hn,1,x)，得到的y就是滤波后的信号了。

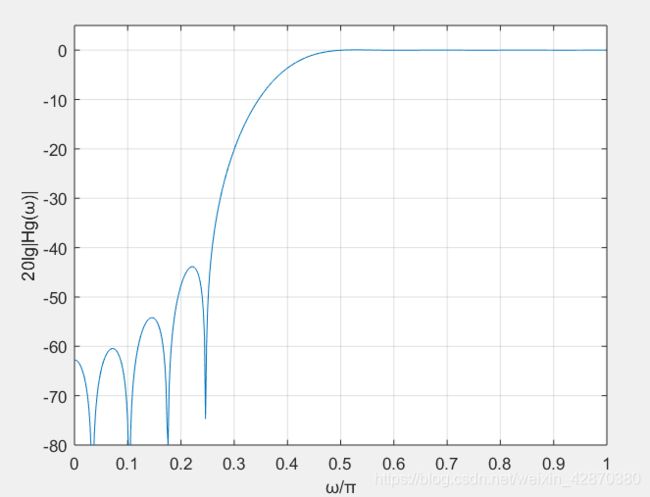
接着我们画出数字高通滤波器的幅频特性曲线，代码如下：

%以下是绘图部分
%计算hn的1024点fft，即求其幅频特性
M=1024;
hk=fft(hn,M);
 
%1024点对应2pi，512点对应pi，我们在1-pi之间取点，求出该点的幅度
k=1:M/2;
fd = abs(hk(k));
 
%横坐标对pi归一化一下，表示起来更清楚，对pi归一化就是0-511 对 M/2归一化
w=(0:M/2-1)/(M/2);
 
figure;
plot(w,20*log10(fd));
axis([0,1,-80,5]);
xlabel('ω/π');ylabel('20lg|Hg(ω)|');
grid on

结果如下：

4. 带通数字滤波器设计

例： 设计线性相位带阻滤波器，通带下频率wpl = 0.35 pi，通带上截止频率wpu = 0.65 pi，，通带衰减Rp = 1dB,阻带下截止频率wsl = 0.2pi，阻带上截止频率wsu = 0.8pi,阻带衰减As=60dB。

由于此处阻带衰减为60dB，所以我们选用 布莱克曼窗

过渡带带宽为 $B_t=w_{pl}-w_{sl}=0.15\pi$

$$N\ge \frac{12\pi }{B_t}=\frac{12\pi }{0.25\pi }=80$$

这里我们取窗口长度 N=80。

归一化后的截止频率 wc=[(wpl+wsl)/2/pi, (wpu+wsu)/2/pi]；

代码如下：

%带通滤波器
wpl = 0.35 * pi;
wpu = 0.65 * pi;
Rp = 1;
wsl = 0.2 * pi;
wsu = 0.8 * pi;
As = 60;
 
DB=wpl-wsl;           %计算过渡带宽度
N=ceil(12*pi/DB); %计算所需h(n)长度N
 
wc=[(wpl+wsl)/2/pi, (wpu+wsu)/2/pi];    %计算带通滤波器截止频率(关于π归一化）
hn=fir1(N-1,wc,blackman(N));  %调用fir1计算带通滤波器参数

至此，FIR数字带通滤波器设计完成了

如果有输入噪声信号x的话，调用y = filter(hn,1,x)，得到的y就是滤波后的信号了。

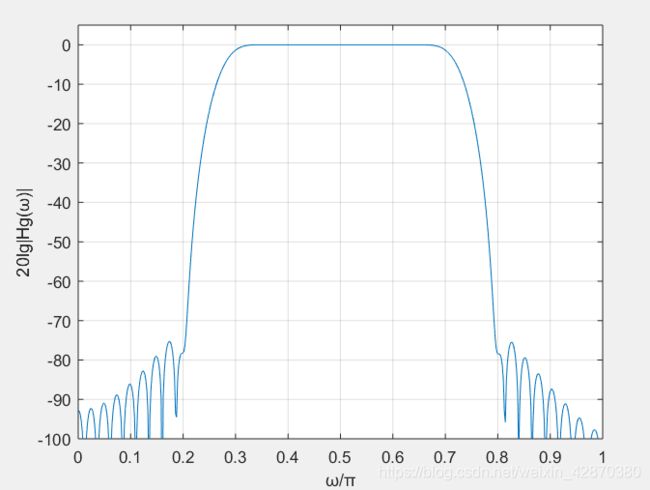
接着我们画出数字带通滤波器的幅频特性曲线，代码如下：

%以下是绘图部分
%计算hn的1024点fft，即求其幅频特性
M=1024;
hk=fft(hn,M);
 
%1024点对应2pi，512点对应pi，我们在1-pi之间取点，求出该点的幅度
k=1:M/2;
fd = abs(hk(k));
 
%横坐标对pi归一化一下，表示起来更清楚，对pi归一化就是0-511 对 M/2归一化
w=(0:M/2-1)/(M/2);
 
figure;
plot(w,20*log10(fd));
axis([0,1,-100,5]);
xlabel('ω/π');ylabel('20lg|Hg(ω)|');
grid on

绘图结果如下：

5. 带阻数字滤波器设计

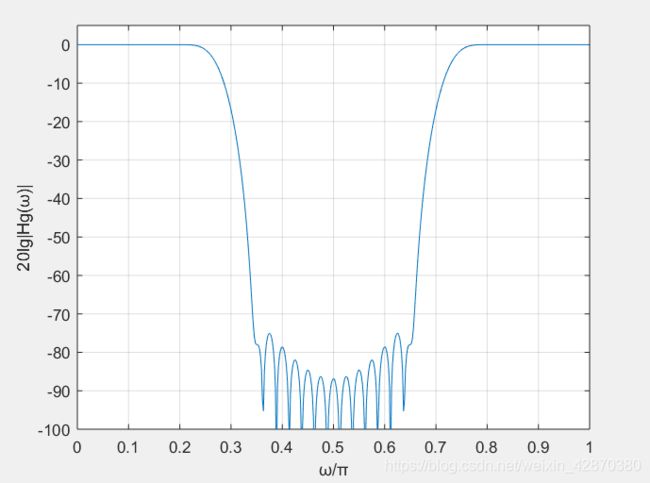
例： 设计线性相位带阻滤波器，通带下频率wpl = 0.2 pi，通带上截止频率wpu = 0.8 pi，，通带衰减Rp = 1dB,阻带下截止频率wsl = 0.35pi，阻带上截止频率wsu = 0.65pi,阻带衰减As=60dB。

由于此处阻带衰减为 60dB ，所以我们选用布莱克曼窗

过渡带带宽为 $B_t=w_{sl}-w_{pl}=0.15\pi$

$$N\ge \frac{12\pi }{B_t}=\frac{12\pi }{0.25\pi }=80$$

由于设计的是带阻滤波器，N需要为奇数，所以这里我们取窗口长度N=81。

归一化后的截止频率 wc=[(wpl+wsl)/2/pi, (wpu+wsu)/2/pi]；

代码如下：

%带阻滤波器
wpl = 0.2 * pi;
wpu = 0.8 * pi;
Rp = 1;
wsl = 0.35 * pi;
wsu = 0.65 * pi;
As = 60;
 
 
DB=wsl-wpl;           %计算过渡带宽度
N0=ceil(12*pi/DB); %计算所需h(n)长度N
 
N = N0 + mod(N0+1,2); %N需要为奇数
 
wc=[(wpl+wsl)/2/pi, (wpu+wsu)/2/pi];    %计算带阻滤波器截止频率(关于π归一化）
hn=fir1(N-1,wc,'stop',blackman(N));  %调用fir1计算带阻滤波器参数

至此，FIR数字带阻滤波器设计完成了

如果有输入噪声信号x的话，调用y = filter(hn,1,x)，得到的y就是滤波后的信号了。

接着我们画出数字带阻滤波器的幅频特性曲线，代码如下：

%以下是绘图部分
%计算hn的1024点fft，即求其幅频特性
M=1024;
hk=fft(hn,M);
 
%1024点对应2pi，512点对应pi，我们在1-pi之间取点，求出该点的幅度
k=1:M/2;
fd = abs(hk(k));
 
%横坐标对pi归一化一下，表示起来更清楚，对pi归一化就是0-511 对 M/2归一化
w=(0:M/2-1)/(M/2);
 
figure;
plot(w,20*log10(fd));
axis([0,1,-100,5]);
xlabel('ω/π');ylabel('20lg|Hg(ω)|');
grid on

绘图结果如下：