用匈牙利算法求二分图的最大匹配

 

转载大神的！！

什么是二分图，什么是二分图的最大匹配，这些定义我就不讲了，网上随便都找得到。二分图的最大匹配有两种求法，第一种是最大流（我在此假设读者已有网络流的知识）；第二种就是我现在要讲的匈牙利算法。这个算法说白了就是最大流的算法，但是它跟据二分图匹配这个问题的特点，把最大流算法做了简化，提高了效率。匈牙利算法其实很简单，但是网上搜不到什么说得清楚的文章。所以我决定要写一下。 
最大流算法的核心问题就是找增广路径（augment path）。匈牙利算法也不例外，它的基本模式就是：

初始时最大匹配为空 
while 找得到增广路径 
do 把增广路径加入到最大匹配中去 
可见和最大流算法是一样的。但是这里的增广路径就有它一定的特殊性，下面我来分析一下。 
（注：匈牙利算法虽然根本上是最大流算法，但是它不需要建网络模型，所以图中不再需要源点和汇点，仅仅是一个二分图。每条边也不需要有方向。）

image图1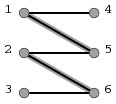

image图2

图1是我给出的二分图中的一个匹配：［1，5］和［2，6］。图2就是在这个匹配的基础上找到的一条增广路径：3->6->2->5->1->4。我们借由它来描述一下二分图中的增广路径的性质：

(1)有奇数条边。 
(2)起点在二分图的左半边，终点在右半边。 
(3)路径上的点一定是一个在左半边，一个在右半边，交替出现。（其实二分图的性质就决定了这一点，因为二分图同一边的点之间没有边相连，不要忘记哦。） 
(4)整条路径上没有重复的点。 
(5)起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。（如图1、图2所示，［1，5］和［2，6］在图1中是两对已经配好对的点；而起点3和终点4目前还没有与其它点配对。） 
(6)路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。（如图1、图2所示，原有的匹配是［1，5］和［2，6］，这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。） 
(7)最后，也是最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。（如图2所示，新的匹配就是所有蓝色的边，而所有红色的边则从原匹配中删除。则新的匹配数为3。）

不难想通，在最初始时，还没有任何匹配时，图1中的两条灰色的边本身也是增广路径。因此在这张二分图中寻找最大配匹的过程可能如下：

(1)找到增广路径1->5，把它取反，则匹配数增加到1。 
(2)找到增广路径2->6，把它取反，则匹配数增加到2。 
(3)找到增广路径3->6->2->5->1->4，把它取反，则匹配数增加到3。 
(4)再也找不到增广路径，结束。

当然，这只是一种可能的流程。也可能有别的找增广路径的顺序，或者找到不同的增广路径，最终的匹配方案也可能不一样。但是最大匹配数一定都是相同的。

对于增广路径还可以用一个递归的方法来描述。这个描述不一定最准确，但是它揭示了寻找增广路径的一般方法： 
“从点A出发的增广路径”一定首先连向一个在原匹配中没有与点A配对的点B。如果点B在原匹配中没有与任何点配对，则它就是这条增广路径的终点；反之，如果点B已与点C配对，那么这条增广路径就是从A到B，再从B到C，再加上“从点C出发的增广路径”。并且，这条从C出发的增广路径中不能与前半部分的增广路径有重复的点。

比如图2中，我们要寻找一条从3出发的增广路径，要做以下3步： 
(1)首先从3出发，它能连到的点只有6，而6在图1中已经与2配对，所以目前的增广路径就是3->6->2再加上从2出发的增广路径。 
(2)从2出发，它能连到的不与前半部分路径重复的点只有5，而且5确实在原匹配中没有与2配对。所以从2连到5。但5在图1中已经与1配对，所以目前的增广路径为3->6->2->5->1再加上从1出发的增广路径。 
(3)从1出发，能连到的不与自已配对并且不与前半部分路径重复的点只有4。因为4在图1中没有与任何点配对，所以它就是终点。所以最终的增广路径是3->6->2->5->1->4。

但是严格地说，以上过程中从2出发的增广路径（2->5->1->4）和从1出发的增广路径（1->4）并不是真正的增广路径。因为它们不符合前面讲过的增广路径的第5条性质，它们的起点都是已经配过对的点。我们在这里称它们为“增广路径”只是为了方便说明整个搜寻的过程。而这两条路径本身只能算是两个不为外界所知的子过程的返回结果。 
显然，从上面的例子可以看出，搜寻增广路径的方法就是DFS，可以写成一个递归函数。当然，用BFS也完全可以实现。

至此，理论基础部份讲完了。但是要完成匈牙利算法，还需要一个重要的定理：

如果从一个点A出发，没有找到增广路径，那么无论再从别的点出发找到多少增广路径来改变现在的匹配，从A出发都永远找不到增广路径。

要用文字来证明这个定理很繁，话很难说，要么我还得多画一张图，我在此就省了。其实你自己画几个图，试图举两个反例，这个定理不难想通的。（给个提示。如果你试图举个反例来说明在找到了别的增广路径并改变了现有的匹配后，从A出发就能找到增广路径。那么，在这种情况下，肯定在找到别的增广路径之前，就能从A出发找到增广路径。这就与假设矛盾了。） 
有了这个定理，匈牙利算法就成形了。如下：

初始时最大匹配为空 
for 二分图左半边的每个点i 
do 从点i出发寻找增广路径。如果找到，则把它取反（即增加了总了匹配数）。 
如果二分图的左半边一共有n个点，那么最多找n条增广路径。如果图中共有m条边，那么每找一条增广路径（DFS或BFS）时最多把所有边遍历一遍，所花时间也就是m。所以总的时间大概就是O（n * m）。

在UVA上，二分图匹配的题目有670和10080，祝好运。

以下是我的标程。是用BFS搜索增广路径的。虽然DFS可能写起来比较简单，但是我不想让它递归很多层。 
欢迎使用我的标程。

 

/////////////////////////////////////////////////////////////////////

//Bipartite graphic and maximum matching with Hungarian algorithm.

/////////////////////////////////////////////////////////////////////

#include <list>

#include <cstring>



using namespace std;



const int MAX_LEFT = 500;

const int MAX_RIGHT = 500;



class Bipartite {

private:

    struct Edge {

        int to;

        Edge* next;



        Edge(int _to) {

            to = _to;

        }

    };



    Edge* m_adjList[MAX_LEFT];

    int m_lCnt;

    int m_rCnt;

    int m_lMatchR[MAX_RIGHT];

    int m_rMatchL[MAX_LEFT];

    int m_preL[MAX_LEFT];

    bool m_visitR[MAX_RIGHT];

    //This matrix is just used to prevent adding two repeated edges.

    bool m_matrix[MAX_LEFT][MAX_RIGHT];



    void clear() {

        for (int i = 0; i < m_lCnt; i++) {

            Edge* e = m_adjList[i];

            while (e != NULL) {

                Edge* pre = e;

                e = e->next;

                delete pre;

            }

            m_adjList[i] = NULL;

        }

        memset(m_matrix, 0, sizeof(m_matrix));

    }



    void findAugment(int start) {

        for (int i = 0; i < m_lCnt; i++) {

            m_preL[i] = -1;

        }

        memset(m_visitR, 0, sizeof(bool) * m_rCnt);

        list<int> que;

        que.push_back(start);

        bool found = false;

        while (!que.empty() && !found) {

            int from = que.front();

            que.pop_front();

            Edge* edge = m_adjList[from];

            while (edge != NULL && !found) {

                int to = edge->to;

                if (!m_visitR[to]) {

                    m_visitR[to] = true;

                    if (m_rMatchL[to] == -1) {

                        found = true;

                        reverse(from, to);

                    }

                    else {

                        que.push_back(m_rMatchL[to]);

                        m_preL[m_rMatchL[to]] = from;

                    }

                }

                edge = edge->next;

            }

        }

    }



    void reverse(int left, int right) {

        m_rMatchL[right] = left;

        while(m_preL[left] != -1) {

            int nextR = m_lMatchR[left];

            m_rMatchL[nextR] = m_preL[left];

            m_lMatchR[left] = right;

            left = m_preL[left];

            right = nextR;

        }

        m_lMatchR[left] = right;

    }



public:

    Bipartite() {

        memset(m_adjList, 0, sizeof(m_adjList));

        m_lCnt = 0;

        m_rCnt = 0;

    }



    ~Bipartite() {

        clear();

    }



    //Add an edge between vertex "left" and "right" while "left" and "right" are

    //the indices of two vertices in the left/right parts of the graph. Indices

    //in the left and right parts are separated and they both begin from 0.

    void addEdge(int left, int right) {

        if (!m_matrix[left][right]) {

            m_matrix[left][right] = true;

            Edge* newEdge = new Edge(right);

            newEdge->next = m_adjList[left];

            m_adjList[left] = newEdge;

        }

    }



    //Before invoking this function, "maxMatch()" must be invoked. This function

    //returns the index of the matching vertex of "left" while "left" is the

    //index of a vertex in the left part of the graphic.

    int getLMatchR(int left) const {

        return m_lMatchR[left];

    }



    //See "getLMatchR()", and this function is opposite to it.

    int getRMatchL(int right) const {

        return m_rMatchL[right];

    }



    void init(int leftCnt, int rightCnt) {

        clear();

        m_lCnt = leftCnt;

        m_rCnt = rightCnt;

        for (int i = 0; i < m_lCnt; i++) {

            m_lMatchR[i] = -1;

        }

        for (int i = 0; i < m_rCnt; i++) {

            m_rMatchL[i] = -1;

        }

    }



    int maxMatch() {

        for (int i = 0; i < m_lCnt; i++) {

            findAugment(i);

        }

        int result = 0;

        for (int i = 0; i < m_lCnt; i++) {

            if (m_lMatchR[i] != -1) {

                result++;

            }

        }

        return result;

    }

};



//Test suites.

#include <iostream>



int main() {

    Bipartite match;

    match.init(300, 400);

    int a[] = {0, 0, 1, 1, 2, 2, 2};

    int b[] = {1, 2, 1, 3, 0, 1, 2};

    for (int i = 0; i < 7; i++) {

        match.addEdge(a[i], b[i]);

    }

    int maxMatch = match.maxMatch();

    cout << maxMatch << " ";

    for (int i = 0; i < 3; i++) {

        cout << match.getLMatchR(i) << " ";

    }

    for (int i = 0; i < 4; i++) {

        cout << match.getRMatchL(i) << " ";

    }

    cout << endl;//Correct: 3 2 3 1 -1 2 0 1

    return 0;

}

View Code

 

补充定义和定理：

最大匹配数：最大匹配的匹配边的数目
最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择
最大独立数：选取最多的点，使任意所选两点均不相连
最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。

定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）
定理2：最大匹配数 = 最大独立数
定理3：最小路径覆盖数 = 顶点数 - 最大匹配数