机器学习 数据预处理之特征缩放（理论+案例）

特征缩放

原因：

• 数量级的差异将导致量级较大的属性占据主导地位
• 数量级的差异将导致迭代收敛速度减慢
• 依赖于样本距离的算法对于数据的数量级非常敏感

好处：

• 提升模型的精度：在机器学习算法的目标函数中使用的许多元素（例如支持向量机的 RBF 内核或线性模型的 l1 和 l2 正则化)，都是假设所有的特征都是零均值并且具有同一阶级上的方差。如果某个特征的方差比其他特征大几个数量级，那么它就会在学习算法中占据主导位置，导致学习器并不能像我们期望的那样，从其他特征中学习
• 提升收敛速度：对于线性模型来说，数据归一化后，寻找最优解的过程明显会变得平缓，更容易正确地收敛到最优解

Standardization (Z-score normalization)

通过减去均值然后除以标准差，将数据按比例缩放，使之落入一个小的特定区间，处理后的数据均值为0，标准差为1

$$x^{\prime }=\frac{x-mean(x)}{std(x)}$$

适用范围：

• 数据本身的分布就服从正太分布
• 最大值和最小值未知的情况，或有超出取值范围的离群数据的情况
• 在分类、聚类算法中需要使用距离来度量相似性、或者使用PCA（协方差分析）技术进行降维时，使用该方法表现更好

Rescaling (min-max normalization)

将原始数据线性变换到用户指定的最大-最小值之间，处理后的数据会被压缩到 [0,1] 区间上

$$x^{\prime }=\frac{x-min(x)}{max(x)-min(x)}$$

适用范围：

• 对输出范围有要求
• 数据较为稳定，不存在极端的最大最小值
• 在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用该方法

Mean normalization

$$x^{\prime }=\frac{x-mean(x)}{max(x)-min(x)}$$

Scaling to unit length

将某一特征的模长转化为1

$$x^{\prime }=\frac{x}{||x||}$$

案例

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.naive_bayes import GaussianNB
from sklearn import metrics
%matplotlib inline

df = pd.read_csv(
    'wine_data.csv',  # 葡萄酒数据集
     header=None,     # 自定义列名
     usecols=[0,1,2]  # 返回一个子集
    )
df.columns = ['Class label', 'Alcohol', 'Malic acid'] # 类别标签、酒精、苹果酸
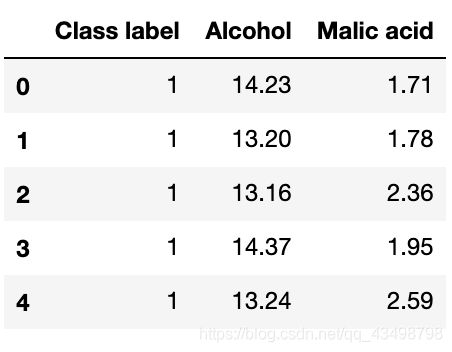
df.head()

如上表所示，酒精（百分含量/体积含量）和苹果酸（克/升）的测量是在不同的尺度上进行的，因此在对这些数据进行任何比较或组合之前，必须先进行特征缩放

# Standardization
std_scale = preprocessing.StandardScaler().fit(df[['Alcohol', 'Malic acid']])
df_std = std_scale.transform(df[['Alcohol', 'Malic acid']])

# Min-Max scaling
minmax_scale = preprocessing.MinMaxScaler().fit(df[['Alcohol', 'Malic acid']])
df_minmax = minmax_scale.transform(df[['Alcohol', 'Malic acid']])

# 均值、标准差
print('Mean after standardization:\nAlcohol={:.2f}, Malic acid={:.2f}'
      .format(df_std[:,0].mean(), df_std[:,1].mean()))
print('\nStandard deviation after standardization:\nAlcohol={:.2f}, Malic acid={:.2f}'
      .format(df_std[:,0].std(), df_std[:,1].std()))

Mean after standardization:
Alcohol=-0.00, Malic acid=-0.00

Standard deviation after standardization:
Alcohol=1.00, Malic acid=1.00

# 最小值、最大值
print('Min-value after min-max scaling:\nAlcohol={:.2f}, Malic acid={:.2f}'
      .format(df_minmax[:,0].min(), df_minmax[:,1].min()))
print('\nMax-value after min-max scaling:\nAlcohol={:.2f}, Malic acid={:.2f}'
      .format(df_minmax[:,0].max(), df_minmax[:,1].max()))

Min-value after min-max scaling:
Alcohol=0.00, Malic acid=0.00

Max-value after min-max scaling:
Alcohol=1.00, Malic acid=1.00

def plot():
    plt.figure(figsize=(8,6))

    plt.scatter(df['Alcohol'], df['Malic acid'], 
            color='green', label='input scale', alpha=0.5)

    plt.scatter(df_std[:,0], df_std[:,1], color='red', 
            label='Standardized [$N  (\mu=0, \; \sigma=1)$]', alpha=0.3)

    plt.scatter(df_minmax[:,0], df_minmax[:,1], 
            color='blue', label='min-max scaled [min=0, max=1]', alpha=0.3)

    plt.title('Alcohol and Malic Acid content of the wine dataset')
    plt.xlabel('Alcohol')
    plt.ylabel('Malic Acid')
    plt.legend(loc='upper left')
    plt.grid()
    
    plt.tight_layout()

plot()
plt.show()

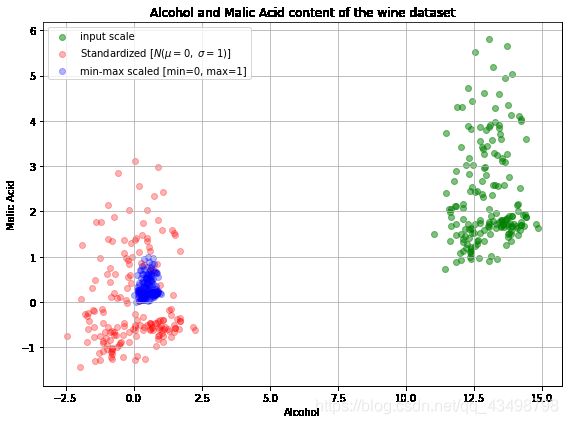
上面的图包括所有三个不同尺度上的葡萄酒数据点：非标准化数据（绿色），z-score标准化后的数据（红色）和max-min标准化后的数据（蓝色）

df['Class label'].value_counts().sort_index()

1 59
2 71
3 48
Name: Class label, dtype: int64

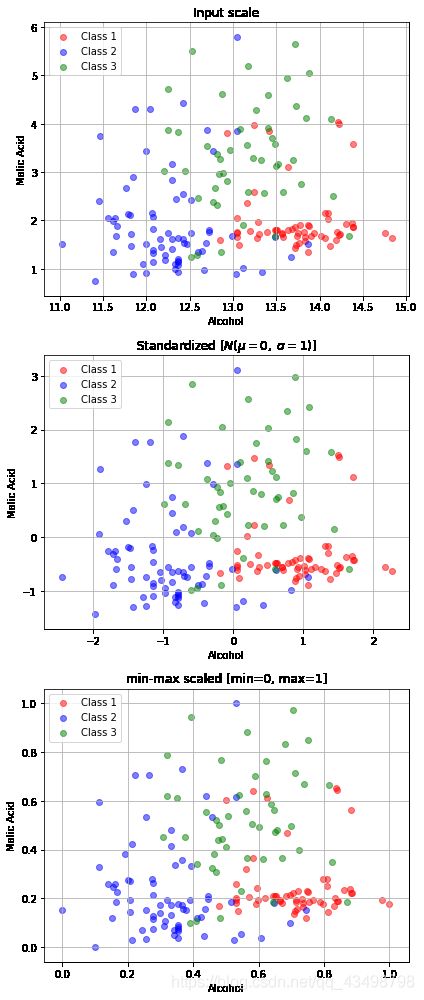
fig, ax = plt.subplots(3, figsize=(6,14))

for a,d,l in zip(range(len(ax)), 
               (df[['Alcohol', 'Malic acid']].values, df_std, df_minmax),
               ('Input scale', 
                'Standardized [$N  (\mu=0, \; \sigma=1)$]', 
                'min-max scaled [min=0, max=1]')
                ):
    for i,c in zip(range(1,4), ('red', 'blue', 'green')):
        ax[a].scatter(d[df['Class label'].values == i, 0], 
                  d[df['Class label'].values == i, 1],
                  alpha=0.5,
                  color=c,
                  label='Class %s' %i
                  )
    ax[a].set_title(l)
    ax[a].set_xlabel('Alcohol')
    ax[a].set_ylabel('Malic Acid')
    ax[a].legend(loc='upper left')
    ax[a].grid()
    
plt.tight_layout()
plt.show()

在机器学习中，如果我们对训练集做了上述处理，那么测试集也必须要经过相同的处理

std_scale = preprocessing.StandardScaler().fit(X_train)
X_train = std_scale.transform(X_train)
X_test = std_scale.transform(X_test)

标准化处理对PCA的影响

以主成分分析（PCA）为例，标准化是至关重要的，因为它可以分析不同特征的差异

读取数据集

df = pd.read_csv(
    'wine_data.csv', 
    header=None,
    )
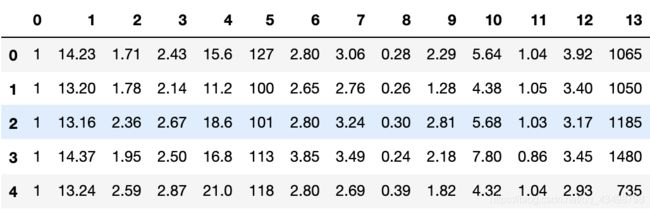
df.head()

划分训练集和测试集

# 将70%的样本作为训练集，30%作为测试集
X_wine = df.values[:,1:]
y_wine = df.values[:,0]

X_train, X_test, y_train, y_test = train_test_split(X_wine, y_wine,
    test_size=0.30, random_state=12345)

特征缩放

# Standardization
std_scale = preprocessing.StandardScaler().fit(X_train)
X_train_std = std_scale.transform(X_train)
X_test_std = std_scale.transform(X_test)

使用PCA进行降维

对标准化和非标准化数据集执行PCA，将数据集转换为二维特征子空间

# on non-standardized data
pca = PCA(n_components=2).fit(X_train)
X_train = pca.transform(X_train)
X_test = pca.transform(X_test)

# om standardized data
pca_std = PCA(n_components=2).fit(X_train_std)
X_train_std = pca_std.transform(X_train_std)
X_test_std = pca_std.transform(X_test_std)

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(10,4))

for l,c,m in zip(range(1,4), ('blue', 'red', 'green'), ('^', 's', 'o')):
    ax1.scatter(X_train[y_train==l, 0], X_train[y_train==l, 1],
        color=c, 
        label='class %s' %l, 
        alpha=0.5,
        marker=m
        )

for l,c,m in zip(range(1,4), ('blue', 'red', 'green'), ('^', 's', 'o')):
    ax2.scatter(X_train_std[y_train==l, 0], X_train_std[y_train==l, 1],
        color=c, 
        label='class %s' %l, 
        alpha=0.5,
        marker=m
        )

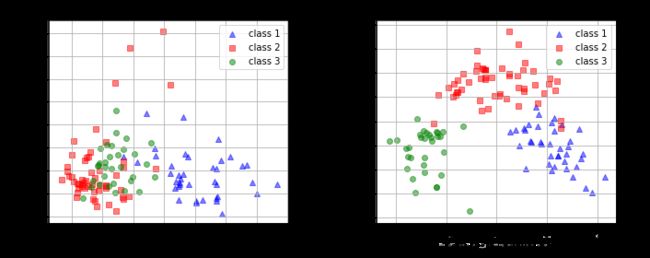
ax1.set_title('Transformed NON-standardized training dataset after PCA')    
ax2.set_title('Transformed standardized training dataset after PCA')    
    
for ax in (ax1, ax2):

    ax.set_xlabel('1st principal component')
    ax.set_ylabel('2nd principal component')
    ax.legend(loc='upper right')
    ax.grid()
    
plt.tight_layout()
plt.show()  

训练朴素的贝叶斯分类器

贝叶斯公式：
$$p(w_j|x)=\frac{p(x|w_j)\ast p(w_j)}{p(x)}$$

# on non-standardized data
gnb = GaussianNB()
fit = gnb.fit(X_train, y_train)

# on standardized data
gnb_std = GaussianNB()
fit_std = gnb_std.fit(X_train_std, y_train)

评估有无标准化的分类准确性

pred_train = gnb.predict(X_train)

print('\nPrediction accuracy for the training dataset')
print('{:.2%}'.format(metrics.accuracy_score(y_train, pred_train)))

pred_test = gnb.predict(X_test)

print('\nPrediction accuracy for the test dataset')
print('{:.2%}\n'.format(metrics.accuracy_score(y_test, pred_test)))

Prediction accuracy for the training dataset
81.45%

Prediction accuracy for the test dataset
64.81%

pred_train_std = gnb_std.predict(X_train_std)

print('\nPrediction accuracy for the training dataset')
print('{:.2%}'.format(metrics.accuracy_score(y_train, pred_train_std)))

pred_test_std = gnb_std.predict(X_test_std)

print('\nPrediction accuracy for the test dataset')
print('{:.2%}\n'.format(metrics.accuracy_score(y_test, pred_test_std)))

Prediction accuracy for the training dataset
96.77%

Prediction accuracy for the test dataset
98.15%

---

本文到此结束，后续将会不断更新，如果发现上述有误，请各位大佬及时指正！