多彩的世界,离不开线性代数

1.向量表示

向量是线性代数的基石,基本上所有的知识都是在向量的基础上搭建的,任何一个数学概念都有一个严格的定义,我们来简单的看一下

物理

就像数字一样,向量也是一个表示某些东西的玩意儿.它的特点是在表示数据的时候,还有方向,可能也就是因此得名向量吧,我们常见的向量(物理上)有速度,加速度等等.

• 物理上,我们用有向线段表示向量,所以点是不可以表示向量的

数学

• 在数学中,我们除了用有向线段表示,也可以用点(其实就是坐标原点到点的连线,本质上也是有向线段).

我们有很多表示方法

$$A+B$$
x=(m,n)…

请不要拘泥于我所说,我们来看看更多的向量

如果玩LOL的同学,肯定知道这是什么
我们看到小鱼人的技能栏,{Q,W,E,R,D,F}技能快捷键所构成的,正是向量
QWERDF总共有6项,我们称6为这个向量的维数

tip:

  1.实际上我们能一眼看出某种表达形式是向量即可

  2.从几何上而言,我们知道我们身处的世界是一个三维的空间,超过三维之后,向量就没有几何意义了.

2.向量的加减与数乘

有了向量的,定义了,我们自然要用它来进行相关的运算在处理显示中的问题.

加减

从简单的开始,向量如何进行加减运算呢?

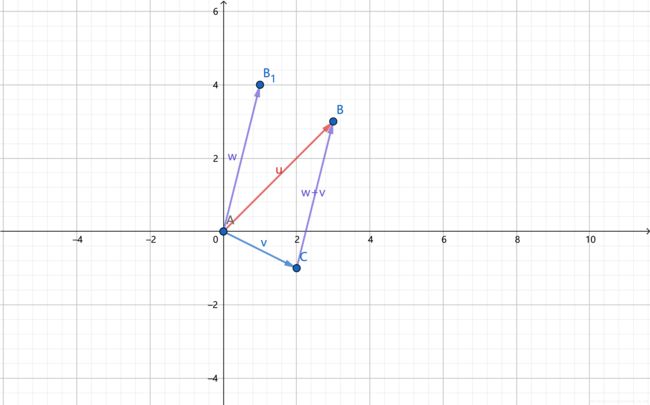
• 在坐标中来看,向量V+W如图,用代数来表示可以写做
• V+W=(U1+U2)+(V1+V2)=(U1+V1,U2+V2)

数乘

直接看图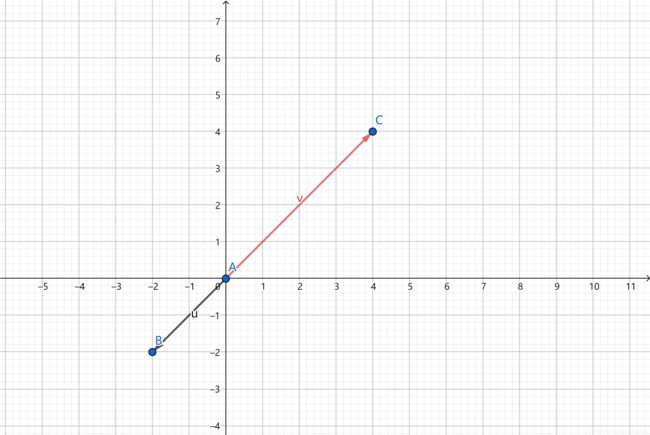
图中,
-2U = V
简单来说就是,数乘为一个带方向的同比缩放

加减数乘并没有改变向量的维数

3.向量的线性组合与线性相关

线性组合

大家都应该看到过电脑中显示颜色时的一些奇怪的代码例如:

这就是用RGB调出来的颜色

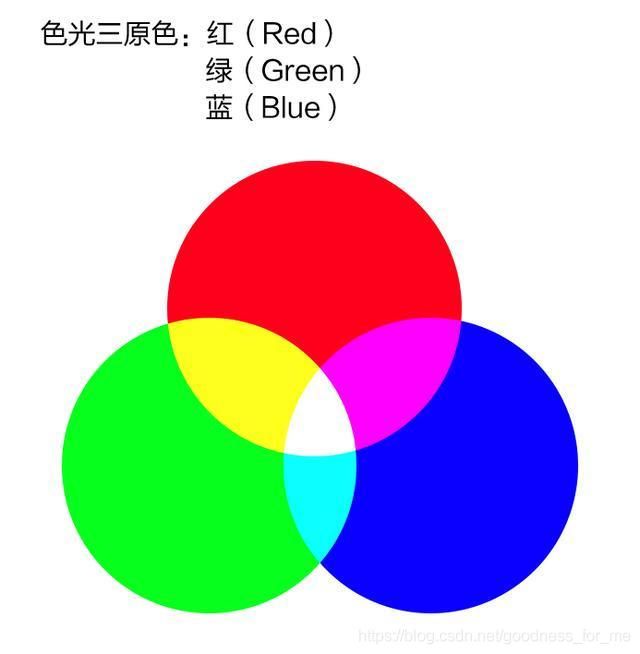
每一个颜色下有6个数字或者字母构成的代码,每两个构成一个16进制数,它代表了这个颜色中R,G,B中各个颜色所占的比重

• 首先我们用向量来表示上面的东西
• 我们定义{R,G,B} = {(255,0,0),(255,0,0),(255,0,0)},其中有三个向量,分别代表了红,绿,蓝三种颜色,我们称{R,G,B}为一个向量组,为了方便构建更深层的知识,我们说其中的向量都是同一维度的.

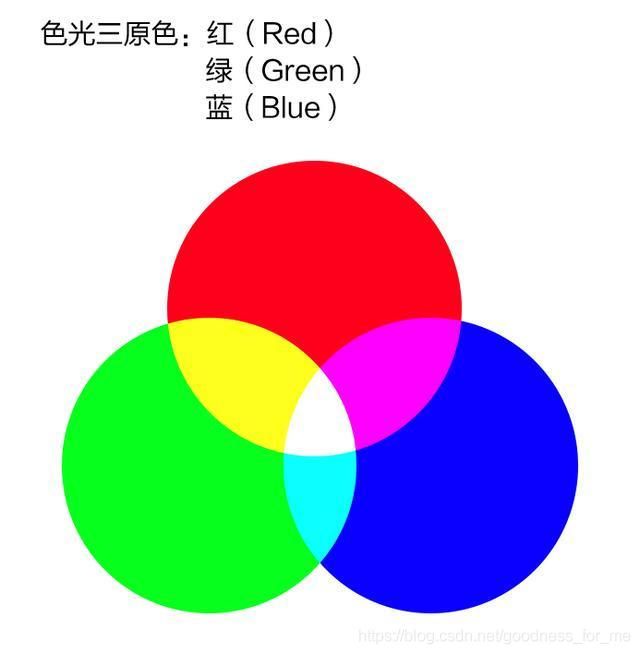
我们还是看到这一张图
由图可知,黄色是由红色和绿色等比混合而成
即
$$黄=红+绿$$

前面我们已经将红和绿量化了,也就是说,经过了加减运算,黄色也是一个向量,并且,黄色可以由红色与绿色表示,我们称
向量黄可以由向量红和向量绿线性表示.
更一般的定义:(向量B可以由向量组A线性表示)
$$B=K_1{A}_1+...+K_m{A}_m$$

线性相关

有了线性组合的概念有助于我们理解线性相关.
我们先定义,总存在一个不为0的K,使得
$$K_1{A}_1+...+K_m{A}_m!=0$$
反之(若=0),则线性相关.
注意!
上述式子由加减和数乘运算组成.由上文我们知道在几何上,我们将进过伸缩(数乘)过的向量做加减运算,直到只剩下最后两个,如果最后两个相加等于0,那么就说明这两个向量在同一直线上,而且长度相等,方向相反.就像这样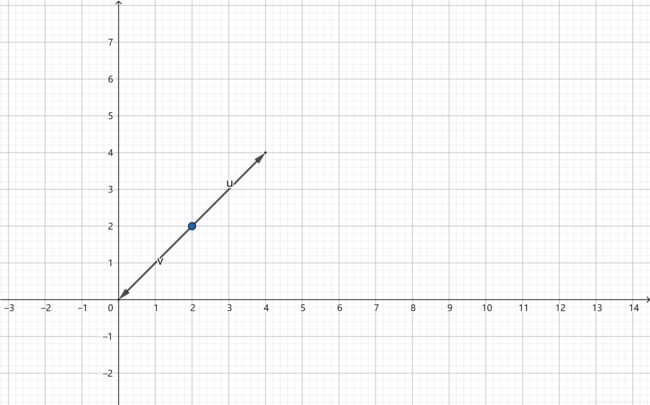
也就说明了向量组A线性相关
还记得前文提到,有了线性组合的概念,我们更好理解线性相关了吗?

• 也就是说,线性组合里面的任意一个向量拿出来,都能被组合里面的其它向量线性表示!

结束

• 线性组合和线性相关的概念非常重要,又他们两定义出了很多其它的概念,诸如最大线性无关组等等
• 请注意,在线性组合的概念中,我们说总有一个以上的K它不等于0,但是并没有说线性表示中的系数K一定不为0,也就是可以所有的系数都为0
• 通过上一条我们不难想象,有零向量存在的向量组一定线性相关.