SLAM练习题（十三）—— 四元数插值

SLAM 学习笔记

四元数在对姿态的描述具有独特的优势，非常适合用来表示空间中的旋转。这主要是因为几个原因：

1. 四元数解决了其他3维空间旋转算法会遇到的恼人的问题，比如使用欧拉角来表示旋转操作时会遇到的万向节锁问题
2. 计算效率比旋转矩阵方法高，因为表达四元数只需要4个数，旋转矩阵需要9个。
3. 其简单的数学表达方式可以被用来规划出高阶连续姿态运动以及在多姿态间插值

以下题目来自计算机视觉life从零开始一起学习SLAM系列

证明四元数线性插值

作业练习1：前面四元数球面线性插值方法比较复杂，下面是它的简化版求解方法，请证明。

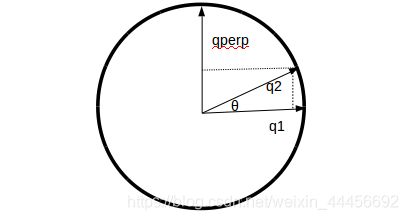
假设v0, v1是两个四元数，其夹角为θ，假设在它们中间进行四元数插值结果为v’，v’和v1之间夹角为θ‘ < θ，记v⊥是垂直于v1的四元数向量，证明：

$$v^{\prime }=v_1\ast cos{\theta }^{\prime }+v\perp \ast sin{\theta }^{\prime }$$

证明：

参考高筒靴整理的答案

实践：图像序列和IMU对齐

代码：

/****************************
 * 题目：四元数球面线性插值
 * 我们用智能手机采集了图像序列和IMU数据，由于IMU帧率远大于图像帧率，需要你用Slerp方法进行四元数插值，使得插值后的IMU和图像帧对齐
 * 已知某帧图像的时间戳为：t =700901880170406，离该图像帧最近的前后两个时刻IMU时间戳为：
 * t1 = 700901879318945，t2 = 700901884127851
 * IMU在t1, t2时刻测量得的旋转四元数为：
 * q1x=0.509339, q1y=0.019188, q1z=0.049596, q1w=0.858921；
 * q2x=0.509443, q2y=0.018806, q2z=0.048944,q2w=0.858905
 * 根据上述信息求IMU对齐到图像帧的插值后的四元数
* 本程序学习目标：
****************************/
#include 
#include 
#include 
#include 
using namespace std;
using namespace cv;
using namespace Eigen;

// 四元数球面线性插值简化方法：v'=v1*cosθ' + v⊥*sinθ'，原理见公众号推送文章
Quaterniond slerp(double t, Quaterniond &q1, Quaterniond &q2)
 {
     
	 // ---- 开始你的代码 ----- //
	q1.normalize();
	q2.normalize();
	 // 四元数变为Mat: 方法 1
//    double q1_array[4] = { q1.w(), q1.x(), q1.y(), q1.z()};
//    double q2_array[4] = { q2.w(), q2.x(), q2.y(), q2.z()};
//    Mat q1_Mat(4,1,CV_64F, q1_array);
//    Mat q2_Mat(4, 1, CV_64F, q2_array);

     // 四元数变为Mat: 方法 2
	Mat q1_Mat = (Mat_<double>(4, 1) << q1.w(), q1.x(), q1.y(), q1.z());
  	Mat q2_Mat = (Mat_<double>(4, 1) << q2.w(), q2.x(), q2.y(), q2.z());
	double dotProd = q1_Mat.dot(q2_Mat);	// q1与q2的点积
	double norm2 = norm(q1_Mat, NORM_L2)*norm(q2_Mat, NORM_L2);	// L2为2范数 即q1的模乘以q2的模
	double cosTheta = dotProd/norm2;	// cosθ = q1.*q2/(||q1||+||q2||)

	Mat result;
	Quaterniond result_quat;
	if(cosTheta>0.9995f)	// 如果θ太小 就使用一元线性插值
	{
     
		result = (1.0f-t)*q1_Mat + t*q2_Mat;
	}else	// 否则就使用球面线性插值的简化方法：v'=v1*cosθ' + v⊥*sinθ'
	{
     
		double theta = acosf(cosTheta);
		double thetaT = theta*t;	// t为0-1的小数 thetaT即为 θ‘
		// q1 q2都为向量，现在要求q1的垂直向量qperp
		// 把q2进行向量分解 q2=qperp*sinθ + q1*cosθ
		// 解出qperp
		Mat qperp = (q2_Mat - cosTheta*q1_Mat)/sinf(theta);	// qperp即为V⊥，即q1的垂直向量
		result = q1_Mat*cosf(thetaT) + qperp*sinf(thetaT);
	}

	result = result / norm(result, NORM_L2);
	// Mat 转化为四元数
	result_quat.w() = result.at<double>(0,0);
	result_quat.x() = result.at<double>(1,0);
	result_quat.y() = result.at<double>(2,0);
	result_quat.z() = result.at<double>(3,0);

	return result_quat;
	// ---- 结束你的代码 ----- //
 }
int main ( int argc, char** argv )
{
     
	double t_img(700901880170406), t1_imu(700901879318945), t2_imu(700901884127851);
	Quaterniond q1 = Quaterniond(0.858921, 0.509339, 0.019188, 0.049596);
	Quaterniond q2 = Quaterniond(0.858905, 0.509443, 0.018806, 0.048944);
	double t = (t_img - t1_imu) / (t2_imu - t1_imu);
    Quaterniond q_slerp = slerp(t, q1, q2);
	cout<<"插值后的四元数：q_slerp =\n"<< q_slerp.coeffs() <<endl;  //coeffs的顺序是(x,y,z,w)
	
    return 0;
}

附CMakeLists.txt

cmake_minimum_required( VERSION 2.8 )
project( slerpQuaternion )
SET(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11 -O3")

include_directories( "/usr/include/eigen3" )
find_package( OpenCV REQUIRED )

include_directories( ${
     OpenCV_INCLUDE_DIRS} )
add_executable( slerpQuaternion slerpQuaternion.cpp )
target_link_libraries( slerpQuaternion ${
     OpenCV_LIBS} )

总结

可以使用Opencv的Mat类中的dot()进行向量的点乘.dot()，使用norm进行向量的归一化：

Mat q1_Mat = (Mat_<double>(4, 1) << q1.w(), q1.x(), q1.y(), q1.z());
  	Mat q2_Mat = (Mat_<double>(4, 1) << q2.w(), q2.x(), q2.y(), q2.z());
	double dotProd = q1_Mat.dot(q2_Mat);	// q1与q2的点积
	double norm2 = norm(q1_Mat, NORM_L2)*norm(q2_Mat, NORM_L2);	// L2为2范数 即q1的模乘以q2的模
	double cosTheta = dotProd/norm2;	// cosθ = q1.*q2/(||q1||+||q2||)

q1的垂直向量求法：

		// q1 q2都为向量，现在要求q1的垂直向量qperp
		// 把q2进行向量分解 q2=qperp*sinθ + q1*cosθ
		// 解出qperp
		Mat qperp = (q2_Mat - cosTheta*q1_Mat)/sinf(theta);	// qperp即为V⊥，即q1的垂直向量

如图所示：

参考：
视觉SLAM14讲
从零开始一起学习SLAM | 用四元数插值来对齐IMU和图像帧