视觉惯性融合学习笔记三 VINS Mono初始化方法
目录
- 一、概述
- 二、VINS-mono初始化方法
- 2.1 符号说明
- 2.2 纯视觉SfM
- 2.3 IMU预积分
- 2.4 视觉惯性匹配
-
- 2.4.1 陀螺仪偏置校正
- 2.4.2 初始化速度、重力和绝对尺度
- 2.4.3 重力细化
这篇笔记会记录论文里的关于初始化的方法,以及自己的一些心得,欢迎交流(o◕∀◕)ノ。
一、概述
这次论文的初始化方法与VI_ORB的初始化方法相似,但是相比之下速度更快,适合需要快速初始化视觉惯性导航系统(VINS)的场合。
二、VINS-mono初始化方法
方法来源:Tong Qin在2017年发表的论文Robust Initialization of Monocular Visual-Inertial
Estimation on Aerial Robots。
Tong Qin在论文里把初始化问题分成3步来解决:(1)陀螺仪偏置估计;(2)速度、绝对尺度和重力粗估计;(3)细化重力。方法和Raul的VI-ORB的初始化方法类似,有需要可以参考我整理的笔记视觉惯性融合学习笔记二 VI_ORB初始化方法。
2.1 符号说明
论文和一般定义变量的方法有些不同,这里先进行符号说明。
( . ) w (.)^{w} (.)w表示世界坐标系,其中z轴和重力平行。这意味着论文的世界坐标系,相当于一般定义的惯性坐标系;
( . ) v (.)^{v} (.)v表示sfm参考坐标系,用于构建视觉结构的固定的坐标系,与惯性坐标系无关。这意味着论文的sfm参考坐标系,相当于一般定义的世界坐标系;
( . ) b (.)^{b} (.)b表示体坐标系;
( . ) b w (.)^{w}_{b} (.)bw表示坐标变换从体坐标系到世界坐标系;
b k b_{k} bk表示第k帧图像对应的体坐标系;
c k c_{k} ck表示第k帧图像对应的相机坐标系;
( . ) ^ \hat{(.)} (.)^表示传感器观测值;
( . ) ˉ \bar{(.)} (.)ˉ表示sfm建立的视觉结构变量;
q q q表示旋转四元数;
g w = [ 0 , 0 , g ] T g^{w}=[0,0,g]^{T} gw=[0,0,g]T表示世界坐标系下重力;
g v g^{v} gv表示sfm参考坐标系下重力;
2.2 纯视觉SfM
与VI_ORB的第一个相似的地方就是都是一种松耦合初始化方法,通过先执行SfM来估计场景结构和相机位姿的初始值。不同的是VI_ORB利用系统开始的固定几秒钟估计结构的初始解和一些关键帧位姿;VINS-Mono则是基于滑动窗口构建视觉结构。(滑动窗口的理论可以参考SLAM中的滑窗(Sliding window))
在这一阶段,VINS-Mono先利用直接法获取两帧间的位姿;然后预设尺度(例如s=1),通过三角测量构建初始地图点;再通过PnP估计窗口内其他帧的位姿;最后用全局BA最小化重投影误差。这样一来,就求得了所有帧的位姿估计 ( p ˉ c k v , q c k v ) (\bar {p}_{c_{k}}^{v}, q_{c_{k}}^{v}) (pˉckv,qckv)和所有观测到的特征的3D坐标估计。如果外参 ( p b c , q b c ) (p_{b}^{c}, q_{b}^{c}) (pbc,qbc)已知,则将所有帧的位姿估计从相机坐标系 c k c_{k} ck转换到对应的体坐标系 b k b_{k} bk:
q b k v = q c k v ⊗ q b c q_{b_{k}}^{v}=q_{c_{k}}^{v} \otimes q_{b}^{c} qbkv=qckv⊗qbc s p ˉ b k v = s p ˉ c k v + q c k v p b c s\bar {p}_{b_{k}}^{v}=s\bar {p}_{c_{k}}^{v}+q_{c_{k}}^{v}p_{b}^{c} spˉbkv=spˉckv+qckvpbc
2.3 IMU预积分
预积分理论可以参考我整理的笔记视觉惯性融合学习笔记一 预积分理论,这里直接写结论。
IMU测量模型为
ω ^ b ( t ) = ω b ( t ) + b g ( t ) + η g ( t ) \hat{\omega} ^{b}(t)=\omega ^{b}(t)+b^{g}(t)+\eta ^{g}(t) ω^b(t)=ωb(t)+bg(t)+ηg(t) a ^ b ( t ) = q b W ( t ) T ( a W ( t ) + g W ) + b a ( t ) + η a ( t ) \hat{a} ^{b}(t)=q_{b}^{W}(t)^{T}(a ^{W}(t)+g^{W})+b^{a}(t)+\eta ^{a}(t) a^b(t)=qbW(t)T(aW(t)+gW)+ba(t)+ηa(t)
连续两帧 b k b_{k} bk到 b k + 1 b_{k+1} bk+1之间的IMU预积分状态量测量值连续形式
α b k + 1 b k = ∬ t ∈ [ k , k + 1 ] γ b t b k a ^ ( t ) d t 2 \alpha _{b_{k+1}}^{b_{k}}=\iint_{t\in [k,k+1]}^{}\gamma _{b_{t}}^{b_{k}}\hat{a}(t)dt^{2} αbk+1bk=∬t∈[k,k+1]γbtbka^(t)dt2 β b k + 1 b k = ∫ t ∈ [ k , k + 1 ] γ b t b k a ^ ( t ) d t \beta _{b_{k+1}}^{b_{k}}=\int_{t\in [k,k+1]}^{}\gamma _{b_{t}}^{b_{k}}\hat{a}(t)dt βbk+1bk=∫t∈[k,k+1]γbtbka^(t)dt γ b k + 1 b k = ∫ t ∈ [ k , k + 1 ] γ b t b k ⊗ [ 1 1 2 ω ^ ( t ) ] d t \gamma _{b_{k+1}}^{b_{k}}=\int_{t\in [k,k+1]}^{} \gamma_{b_{t}}^{b_{k}}\otimes \begin{bmatrix} 1 \\ \frac{1}{2}\hat{\omega}(t) \end{bmatrix}dt γbk+1bk=∫t∈[k,k+1]γbtbk⊗[121ω^(t)]dt
其中 α b k + 1 b k \alpha _{b_{k+1}}^{b_{k}} αbk+1bk, β b k + 1 b k \beta _{b_{k+1}}^{b_{k}} βbk+1bk和 γ b k + 1 b k \gamma _{b_{k+1}}^{b_{k}} γbk+1bk表示IMU预积分的三个测量值。
VINS-mono采用的预积分表示方法和On-Manifold Preintegration for Real-Time Visual–Inertial Odometry不同。其中旋转预积分采用四元数表示。
绕旋转轴 n ⃗ = [ n x , n y , n z ] T \vec{n}=[n_{x},n_{y},n_{z}]^{T} n=[nx,ny,nz]T的角度为 θ \theta θ的旋转用四元数表示为 q = [ c o s θ 2 , n x s i n θ 2 , n y s i n θ 2 , n z s i n θ 2 ] T q=[cos\frac{\theta}{2}, n_{x}sin\frac{\theta}{2},n_{y}sin\frac{\theta}{2},n_{z}sin\frac{\theta}{2}]^{T} q=[cos2θ,nxsin2θ,nysin2θ,nzsin2θ]T。如果 θ \theta θ比较小,四元数可以近似表示为 [ 1 θ 2 n ⃗ ] \begin{bmatrix}1 \\ \frac{\theta}{2}\vec{n}\end{bmatrix} [12θn],然后可以推出上式。
关于四元数的内容推荐阅读论文Quaternion kinematics for the error-state Kalman filter。
2.4 视觉惯性匹配
2.4.1 陀螺仪偏置校正
对窗口内的连续两帧 b k b_{k} bk和 b k + 1 b_{k+1} bk+1,根据2.2的纯视觉SfM可以计算出IMU在世界坐标系下的姿态 q b k + 1 v q _{b_{k+1}}^{v} qbk+1v和 q b k + 1 v q _{b_{k+1}}^{v} qbk+1v;根据2.3的IMU预积分可以计算出连续两帧IMU的姿态变化 γ ^ b k + 1 b k \hat{\gamma} _{b_{k+1}}^{b_{k}} γ^bk+1bk。因此可以建立目标函数
a r g m i n δ b g ∑ k ∈ B ∣ ∣ q b k + 1 v − 1 ⊗ q b k v ⊗ γ b k + 1 b k ∣ ∣ 2 \underset{\delta b_{g}}{argmin} \sum_{k \in B}^{}||{q_{b_{k+1}}^{v}}^{-1}\otimes q_{b_{k}}^{v}\otimes \gamma _{b_{k+1}}^{b_{k}}||^{2} δbgargmink∈B∑∣∣qbk+1v−1⊗qbkv⊗γbk+1bk∣∣2 γ b k + 1 b k ≈ γ ^ b k + 1 b k ⊗ [ 1 1 2 ∂ γ b k + 1 b k ∂ b g δ b g ] \gamma _{b_{k+1}}^{b_{k}} \approx \hat{\gamma}_{b_{k+1}}^{b_{k}}\otimes \begin{bmatrix} 1 \\ \frac{1}{2} \frac{\partial \gamma _{b_{k+1}}^{b_{k}}}{\partial b_{g}} \delta b_{g} \end{bmatrix} γbk+1bk≈γ^bk+1bk⊗[121∂bg∂γbk+1bkδbg]
其中B表示滑动窗口内所有相机帧的索引。
2.4.2 初始化速度、重力和绝对尺度
定义待优化的变量为
χ I = [ v b 0 v , . . . v b n v , g v , s ] \chi _{I}=[v_{b_{0}}^{v},...v_{b_{n}}^{v},g^{v},s] χI=[vb0v,...vbnv,gv,s]
则对于连续两帧相机帧,根据IMU预积分状态量计算值定义(参考视觉惯性融合学习笔记一 预积分理论3.2)可以计算得到
z ^ b k + 1 b k = [ α ^ b k + 1 b k β ^ b k + 1 b k ] = H b k + 1 b k χ I + n b k + 1 b k ≈ [ − q v b k Δ t k 0 1 2 q v b k Δ t k 2 q v b k ( p ˉ b k + 1 v − p ˉ b k v ) − q v b k q v b k q v b k Δ t k 0 ] [ v b k v v b k + 1 v g v s ] \hat{z}_{b_{k+1}}^{b_{k}}= \begin{bmatrix} \hat{\alpha} _{b_{k+1}}^{b_{k}} \\ \hat{\beta} _{b_{k+1}}^{b_{k}} \end{bmatrix} =H_{b_{k+1}}^{b_{k}} \chi _{I}+n_{b_{k+1}}^{b_{k}} \approx \begin{bmatrix} -q_{v}^{b_{k}}\Delta t_{k} & 0 & \frac{1}{2} q_{v}^{b_{k}}\Delta t_{k}^{2} & q_{v}^{b_{k}}(\bar{p}_{b_{k+1}}^{v}-\bar{p}_{b_{k}}^{v}) \\ -q_{v}^{b_{k}} & q_{v}^{b_{k}} & q_{v}^{b_{k}}\Delta t_{k} & 0 \end{bmatrix} \begin{bmatrix} v_{b_{k}}^{v} \\ v_{b_{k+1}}^{v} \\ g^{v} \\ s \end{bmatrix} z^bk+1bk=[α^bk+1bkβ^bk+1bk]=Hbk+1bkχI+nbk+1bk≈[−qvbkΔtk−qvbk0qvbk21qvbkΔtk2qvbkΔtkqvbk(pˉbk+1v−pˉbkv)0]⎣⎢⎢⎡vbkvvbk+1vgvs⎦⎥⎥⎤
其中第一个等号后的 z ^ b k + 1 b k \hat{z}_{b_{k+1}}^{b_{k}} z^bk+1bk表示由IMU测量值计算得到的IMU预积分测量值,第二个等号后的 H b k + 1 b k χ I H_{b_{k+1}}^{b_{k}} \chi _{I} Hbk+1bkχI表示由纯视觉SfM计算得到的IMU预积分计算值; Δ t k \Delta t_{k} Δtk表示连续两帧相机帧之间的时间间隔。
这样可以构建目标函数
a r g m i n χ I ∑ k ∈ B ∣ ∣ z ^ b k + 1 b k − H b k + 1 b k χ I ∣ ∣ 2 \underset{\chi _{I}}{argmin}\sum_{k \in B}^{}||\hat{z}_{b_{k+1}}^{b_{k}}-H_{b_{k+1}}^{b_{k}} \chi _{I}||^{2} χIargmink∈B∑∣∣z^bk+1bk−Hbk+1bkχI∣∣2
其中B表示滑动窗口内所有相机帧的索引。利用高斯牛顿法或者LM法可以估计 χ I \chi _{I} χI。
2.4.3 重力细化
可以利用重力大小细化重力向量。但是直接加入重力大小约束到2.4.2的目标函数会导致问题变得复杂。因此论文将重力重新定义为
g . g ^ ˉ + ω 1 b 1 + ω 2 b 2 g.\bar{\hat{g}}+\omega_{1}b_{1}+\omega_{2}b_{2} g.g^ˉ+ω1b1+ω2b2
其中g表示重力大小, g ^ ˉ \bar{\hat{g}} g^ˉ, b 1 b_{1} b1和 b 2 b_{2} b2为一组标准正交基。这里利用Gram-Schmidt正交化方法,将原SfM参考坐标系下的估计出的重力粗估计投影到一组标准正交向量上;将新的重力初始值代入目标函数,可以求出细化后的重力初始值。这样根据重力向量可以将所有SfM参考坐标系下的变量全部转化到世界坐标系下。到这里VINS-Mono的初始化过程就结束了。
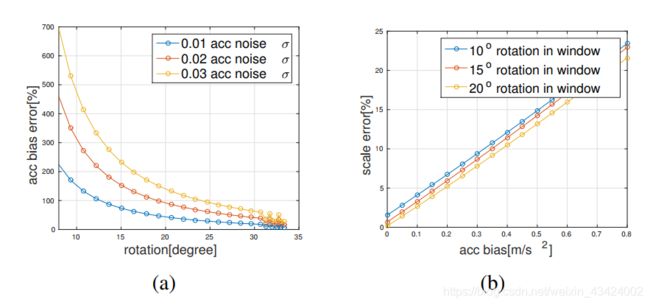
论文最后还针对加速度计偏置进行了两个仿真实验:
1、第一个仿真实验中,飞行器在进行加速运动的同时,进行不同角度的旋转。将 α b k + 1 b k \alpha _{b_{k+1}}^{b_{k}} αbk+1bk, β b k + 1 b k \beta _{b_{k+1}}^{b_{k}} βbk+1bk在加速度计偏置 b a b_{a} ba处线性化,之后代入目标函数进行优化。结果显示只有当旋转角度足够(接近30°)时,才能有效校正 b a b_{a} ba;
2、在第二个仿真实验中,飞行器同样进行加速运动的同时,进行不同角度的旋转。这次仿真忽略加速度计偏置的初始化,执行论文中的初始化过程。结果显示,尺度的初始化误差随着 b a b_{a} ba的增大而增大,并且要产生10%的尺度误差,需要0.3 m / s 2 m/s^{2} m/s2的加速度计偏置,而这个值通常不会达到。
这两个仿真实验说明了论文不在初始化阶段考虑 b a b_{a} ba的原因。仿真结果引用VINS-Mono论文的图3。
以上只是简单介绍了VINS-Mono的初始化流程,具体的过程可以参考论文或者看代码VINS-Mono。