python基于广度优先（BFS）的迪杰斯特拉(Dijkstra)算法 求最短路径

python深度优先与广度优先的遍历算法区别
首先要理解搜索步，一个完整的搜索步包括两个处理：
a) 获得当前位置上，有几条路可供选择
b) 根据选择策略，选择其中一条路，并走到下个位置
广度优先:就是，从初始点出发，把所有可能的路径都走一遍，如果里面没有目标位置，则尝试把所有两步能够到的位置都走一遍，看有没有目标位置；如果还不行，则尝试所有三步可以到的位置。这种方法，一定可以找到一条最短路径，但需要记忆的内容实在很多，要量力而行。
Dijkstra算法图文详解
求最短路径需要引进heapq模块，该模块提供了堆排序算法以及优先队列
详情请查看下列原文
Python标准库模块之heapq

以下为求最短路径 例题
1、计算下图任意两点的最短路径。

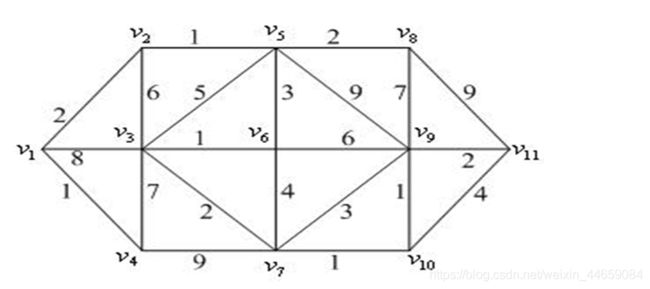
实现代码

import heapq
import math
graph={
     
    "v1":{
     "v2":2,"v3":8,"v4":1},
    "v2":{
     "v1":2,"v3":6,"v5":1},
    "v3":{
     "v1":8,"v2":6,"v4":7,"v5":5,"v6":1,"v7":2},
    "v4":{
     "v1":1,"v3":7,"v7":9},
    "v5":{
     "v2":1,"v3":5,"v6":3,"v8":2,"v9":9},
    "v6":{
     "v3":1,"v5":3,"v7":4,"v9":6},
    "v7":{
     "v3":2,"v4":9,"v6":4,"v9":3,"v10":1},
    "v8":{
     "v5":2,"v9":7,"v11":9},
    "v9":{
     "v5":9,"v6":6,"v7":3,"v8":7,"v10":1,"v11":2},
    "v10":{
     "v7":1,"v9":1,"v11":4},
    "v11":{
     "v8":9,"v9":2,"v10":4}
}
#初始化起点的距离  到自身为零 到其他节点为无穷大
def init_distance(graph,s): #传入图像 和起点
    distance={
     s:0}
    for vertex in graph:
        if vertex !=s:
            distance[vertex]=math.inf  #除到本身都为无穷大
    return distance
def dijkstra(graph,s):
    pqueue=[]     #创建一个队列
    # 先添加一个起点到队列 和后面加入的排序  
    # 此方法把 队列里面的元素按照优先排列 调用heapop时返回优先级最高的   比如数值最小的
    heapq.heappush(pqueue,(0,s))  
    seen=set() #储存出现过的点
    parent={
     s:None}   #标记此节点的上一个节点  此节点为起点 则父节点为None  
    distance=init_distance(graph,s)

    while (len(pqueue)>0):
        pair=heapq.heappop(pqueue)  #返回一个数值最小的元组 
        dist=pair[0]  #提取距离
        vertex=pair[1] #提取节点
        seen.add(vertex) #添加出现过的节点
        nodes=graph[vertex].keys()   #提取与vertex相连的节点
        # print(nodes)
        #核心算法
        for w in nodes:
            if w not in seen:
                 if dist+graph[vertex][w]<distance[w]:
                     #把路径短的添加到队列 并排序
                     heapq.heappush(pqueue,(dist+graph[vertex][w],w))
                     parent[w]=vertex  #记录父节点
                     distance[w]=dist+graph[vertex][w] #更新起点到w节点的距离
    return parent,distance
#测试代码
start, end = input("请输入起止节点用空格分开：").split()
parent,distance=dijkstra(graph,start)
print("父节点列表:",parent)
print("{}到各点的距离:".format(start),distance)
print("{}到{}的距离:".format(start,end),distance[end])

运行结果

如果要求出路径，可以根据父节点parent列表求出路径
实现代码

def distance_path(graph,s,end):
    parent, distance = dijkstra(graph, s)
    path=[end]  
    while parent[end] !=None:
        path.append(parent[end])
        end=parent[end]
    path.reverse()  
    return path

测试代码

#测试代码
start, end = input("请输入起止节点用空格分开：").split()
parent,distance=dijkstra(graph,start)
path=distance_path(graph,start,end)
print("{}到{}的路径:".format(start, end), path)

运行结果

谢谢请关注。