力扣学习笔记 day8

题062.不同路径

题意

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

eg

输入： m = 3, n = 7
输出： 28

---

解题

动态规划

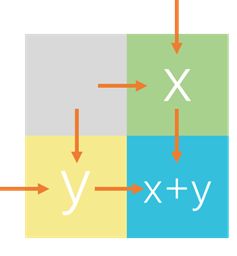
本题有个很重要的地方，就是规定了 移动的方向只能向右或向下，换种思路去理解，

对于一个方块，到达它只能从它的上方或者左方

也就是说， 到达某个方块的路径的数量为到达它上方和左方方块的路线数量之和。

有了这一点，可以去想到通过不断计算从左上到右下的每个方块的路线数量，进而最终得到右下角方块的路线数。

但这边要注意初始化不能进行 左+上 操作的网格的值

1. 定义一个矩阵，大小和题中的网格相同，将最上方的一行和最左侧的一列的值初始化为 1 ，其余节点值为0

helper=[[1]*n]+[[1]+[0]*(n-1) for _ in range(m-1)]

2. 对为0的节点进行逐行计算，直至最后得出目标值

#从helper[1][1]开始
for i in range(1,m):
	 for j in range(1,n):
	 	helper[i][j]=helper[i-1][j]+helper[i][j-1]
return helper[m-1][n-1]

---

题070.爬楼梯

题意

假设需要爬 n 节楼梯，每次爬 1 或 2 节，请问有多少种爬楼方案？

---

解题

看到本题，第一反应就是递归，因为每一次有两种选择，所以走 n 个台阶只能选择 1 + n-1 和 2 + n-2 两种方案，即n个台阶的总方案数 f(n)=f(n-1)+f(n-2) ， 瞬间很熟悉，对，很像斐波那契数列。

所以马上写了个递归提交了：

def climbStairs(self, n: int) -> int:
	if n==1:
		return 1
	elif n==2:
		return 2
	else:
		return self.climbStairs(n-1)+self.climbStairs(n-2)

然后就超时了……，因为这样出现了大量的重复计算，取个较大的n的话可能就算了不知道多少遍的f(2)、f(3)，所以还是用一个循环进行计算比较合适。

if n<3:
	return n
a,b,c=1,2,0
for i in range(3,n+1):
	c=a+b
	a,b=b,c
return c

---

题078.子集

题意

给你一个整数数组 nums ，返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。

eg

输入： nums = [1,2,3]
输出： [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

---

解题

这题可以用递归，也可以用迭代，其实思路是一样的

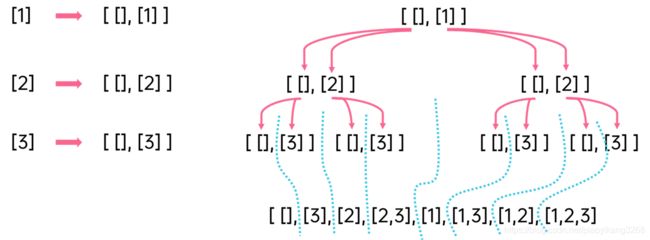
以集合[1,2,3]为例，对于每个数，比如1， 它取不取就是两种情况，空集[] 和集合 [1]，如上图所示

递归

对于当前数：

• 如果取这个数，那么把它和剩余n-1个数的结果结合，加到集合内
• 如果不取，视作空集，被剩余n-1个数的结果加到集合内

具体实现如下：

def subsets(self, nums: List[int]) -> List[List[int]]:
	cur=[]
	if len(nums)==1:
		return [[],[nums[0]]]
	for item in self.subsets(nums[1:]):
		cur.append([]+item)
		cur.append([nums[0]]+item)
	return cur

迭代

迭代的方式代码更简洁一点，其实思路和上方一样，就不多说了。

res=[[]]
for i in nums:
	res=res+[[i]+num for num in res]
return res