神经网络的反向传播算法中矩阵的求导方法(矩阵求导总结)
参考书籍(带书签高清版)的下载链接: https://download.csdn.net/download/zongza/10701105
前言
神经网络的精髓就是反向传播算法,其中涉及到一些矩阵的求导运算,只有掌握了与矩阵相关的求导法则才能真正理解神经网络.
本文以 https://blog.csdn.net/zongza/article/details/82849976 中所示的三层神经网络为例,通过一些简单的法则实现对文中逻辑回归的反向传播推导.
与矩阵有关的求导主要分为两类:
- 标量 f 对 矩阵 W的导数 (其结果是和W同纬度的矩阵,也就是f对W逐元素求导排成与W尺寸相同的矩阵)
- 矩阵 F 对 矩阵 W的导数 (其结果是一个四维的矩阵,这个不是本文关注的重点,因为暂时用不到)
回到博文中提到的神经网络, 这里f 实际上就是loss(神经网络的损失),每个batch的训练集所获得的损失都是一个标量,他是网络参数W和b的函数 (f = LOSS(W,b)),因此想要完成对参数的更新就需要求 L这个标量对W这个矩阵的导数
,在代码中简记为dW,如下所示,本文的目的就是手动完成dW_1和dW_2以及db_1,db_2的推导过程:
#正向传播
Z_1 = np.dot(W_1.T,X) + b_1 # 维度N1*M ,N1表示第一隐层的神经元数
A_1 = sigmoid(Z_1) # 维度N1*M
Z_2 = np.dot(W_2.T,A_1) + b_2 # 维度N2*M ,N2表示输出层的神经元数
A_2 = sigmoid(Z_2) # 维度N2*M
L = cross_entropy(A_2,Y) # 标量(具体实现待研究)
#反向传播
dZ_2 = A_2 - Y # 维度N2*M ,N2表示输出层的神经元数
dW_2 = 1/m* np.dot(dZ_2, A_1.T) # 维度N2*N1
db_2 = 1/m* np.sum(dZ_2,axis = 1,keepdims = true) # 维度N2*1
dZ_1 = np.dot(W_2,dZ_2) * A_1*(1-A_1) # 维度N1*M，注意这里是对sigmoid激活函数的推导，若激活函数变成ReLu则*A_1（大于0的部分）
dW_1 = 1/m* np.dot(dZ_1, X.T) # 维度N1*N0,N0表示单样本的特征数
db_1 = 1/m* np.sum(dZ_1,axis = 1,keepdims = true) # 维度N1*1
1.基础知识
首先回顾一下高数中的导数与微分的知识:
- 一元微积分中的微分df与导数
(标量对标量的导数): 
- 多元微积分中的微分df与梯度
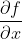(标量对向量的导数):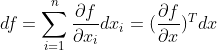 
这里微分与梯度的联系中第一个等号是全微分公式,第二个等号则表明全微分df是由梯度向量
- 受此启发,我们可以将微分df和矩阵导数
(标量对矩阵的导数)视为:
这里,与梯度类似,第一个等号是全微分公式,第二个等号则表明全微分df是由导数矩阵
需要注意的是tr表示矩阵的迹(tarce),是方针对角线元素之和,满足性质：对尺寸相同的矩阵A,B
也即:上式左部可视为矩阵A,B的内积(上式右部),例如:
2.运算法则
回想遇到的较复杂的一元函数.如:
我们是如何求导的呢？通常不是从定义开始求极限，而是先建立了初等函数求导和四则运算、复合等法则，再来运用这些法则。故而，我们来创立常用的矩阵微分的运算法则：
- 加减法:
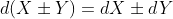
- 乘法: d(XY) = (dX)Y+XdY
- 转置:
- 迹:
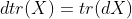
- 逆:
(可由
两侧求微分证明) - 行列式:
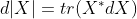其中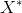
表示X的伴随矩阵,在X可逆时又可以写成
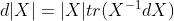此式可用laplace展开证明 - 逐元素乘法:
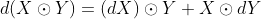其中
表示尺寸相同的矩阵X,Y进行元素乘法 - 逐元素函数:
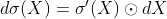其中![\sigma(X) = [\sigma(X_{i,j})]](http://img.e-com-net.com/image/info8/d17e08e45a52444b93f7b3cf7bdbf05b.gif)
是逐元素标量函数计算![{\sigma}'(X) = [{\sigma}'(X_{i,j})]](http://img.e-com-net.com/image/info8/a3c6f5022e07476282772cc9dc1404a8.gif)
是逐元素标量导数计算
这里解释一下逐元素函数和逐元素求导,举个例子:
,那么
![d(sinX) = [cosx_{1}dx_{1},cosx_{2}dx_{2}] = cosX \odot dX](http://img.e-com-net.com/image/info8/38b78843249c4deea18c8e0f89045923.gif)
我们试图利用微分与矩阵导数的联系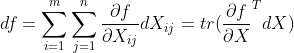在求出左侧的微分后，该如何写成右侧的形式并得到导数呢？这需要一些迹技巧(trace trick)：
- 标量套上迹 : a = tr(a)
- 转置:
- 线性:
- 矩阵乘法交换:
,其中A与
尺寸相同,两侧都等于
- 矩阵乘法/逐元素乘法交换:
其中ABC尺寸相同,两侧都等于
观察一下可以断言: 若标量函数f是矩阵X经加减乘法、行列式、逆、逐元素函数等运算构成，则使用相应的运算法则对f求微分，再使用迹技巧给df套上迹(df是标量tr(df) = df)并将其它项交换至dX左侧，即能得到导数。
3.三层神经网络反向传播推导
假定一共有M个样本,每个样本的特征值有N0个,第一隐层的神经元有N1个,输出层的神经元有N2个 ,正向传播得到损失L(标量)的过程如下:
#正向传播
Z_1 = np.dot(W_1.T,X) + b_1 # 维度N1*M ,N1表示第一隐层的神经元数
A_1 = sigmoid(Z_1) # 维度N1*M
Z_2 = np.dot(W_2.T,A_1) + b_2 # 维度N2*M ,N2表示输出层的神经元数
A_2 = sigmoid(Z_2) # 维度N2*M ,本例中N2=1
L = cross_entropy(A_2,Y) # 标量具体到损失L的计算公式有:
(注:
是一个(M,1)的单位向量,表示求和的操作,这里为了表示方便少写了一个求均值操作(除以M)表示用M个样本的loss均值表示一个batch的loss)
其中Y(N2,M), 是逐元素乘法,N2相当于样本可以分成N2个种类(本例中N2=1,也就是二分类.如果是多元的就得用softmax而不是cross_entropy,最后得到的同样是一个标量,不过公式不同了),M是样本总数.
- 第一步: 求微分dL
其中Y是常矩阵,所以dY和
为零阵,同时由法则知
代入得:
因为我们要求的是
所以需要继续对
进行微分以出现
,由法则可得:
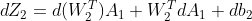
注意这里A1和W2,b_2都是变量,利用法则:d(XY) = (dX)Y+XdY
代入后可得dL:
(1)
(2)
- 第二步: 使用迹技巧将dW换到最右侧
对于(1)式:
已经在最右侧,所以直接进行迹转换可得
因为
与
尺寸相同,所以有:
由法则
根据
,将其和上式最右公式比对知:
也就是代码中: dZ_2 = A_2 - Y
对于(2)式:
并不在子式的最右端,因此需要进行变换(下面公式中db_2的那一项省略了,因为得到
的方法同
):
从+号右边的式子我们可以得到(关于A_1,b_2偏导):
对应代码:db_2 = dZ_2 (均值运算最后再考虑,这里只看求导结果)
对于+号左边还需要继续变形(移动dW到右端)才能得到另一个偏导:
因此,可得:
对应代码中的:dW_2 = np.dot( dZ_2 , A_1.T )
更进一步,为了得到W_1和b_1的偏导,还需要对A_1和Z_1进行微分,留给读者推导.
![dL =tr(dL) = tr(I((A_{2}-Y)\odot dZ_{2})) = tr((I^{T})^{T}((A_{2}-Y)\odot dZ_{2}))= tr([(I^{T})\odot (A_{2}-Y)]^{T} dZ_{2})](http://img.e-com-net.com/image/info8/2f2ffd0f29f743d0b744093e468846c0.gif){kind=small}
![dL = tr(dL) = tr((A_{2}-Y)\odot [d(W_{2}^{T})A_{1}] I+(A_{2}-Y)\odot [W_{2}^{T}dA_{1} ]I)](http://img.e-com-net.com/image/info8/be30a5f01e234197a0564776694957f7.gif){kind=small}
![= tr((A_{2}-Y)\odot [d(W_{2}^{T})A_{1}] I)+tr((A_{2}-Y)\odot [W_{2}^{T}dA_{1}] I)](http://img.e-com-net.com/image/info8/5d1996c652d44801856553f394754e5f.gif){kind=small}
![= tr( I[(A_{2}-Y)\odot {d(W_{2}^{T})A_{1}} ]+tr(I[(A_{2}-Y)\odot W_{2}^{T}dA_{1}])](http://img.e-com-net.com/image/info8/60abf4730ced4d3da725e69b6a6acd5e.gif){kind=small}
![= tr( [I^{T}\odot (A_{2}-Y)]^{T} (dW_{2}^{T}A_{1})) +tr([I^{T}\odot (A_{2}-Y)] ^{T}W_{2}^{T}dA_{1})](http://img.e-com-net.com/image/info8/67769616dbf74a13a3eb69cbd692e07b.gif)
![tr( [I^{T}\odot (A_{2}-Y)]^{T} (dW_{2}^{T}A_{1}))=tr((A_{2}-Y)^T(A_1^TdW_2)^T)](http://img.e-com-net.com/image/info8/f637fbbb514948379db3df1073d72ea3.gif){kind=small}
![= tr([(A_1^TdW_2)(A_{2}-Y)]^T) = tr((A_1^TdW_2)(A_{2}-Y))=tr((A_{2}-Y)(A_1^TdW_2))](http://img.e-com-net.com/image/info8/6a8fa036e848402db71a80846b263237.gif){kind=small}
综上可得反向传播过程是:
#反向传播
dZ_2 = A_2 - Y # 维度N2*M ,N2表示输出层的神经元数
dW_2 = 1/m* np.dot(dZ_2, A_1.T) # 维度N2*N1
db_2 = 1/m* np.sum(dZ_2,axis = 1,keepdims = true) # 维度N2*1
dZ_1 = np.dot(W_2,dZ_2) * A_1*(1-A_1) # 维度N1*M
dW_1 = 1/m* np.dot(dZ_1, X.T) # 维度N1*N0,N0表示单样本的特征数
db_1 = 1/m* np.sum(dZ_1,axis = 1,keepdims = true) # 维度N1*1
4.更多矩阵求导的实例
1: ,求其中是列向量，是矩阵，是列向量，是标量。
先使用矩阵乘法法则求微分，这里的是常量，，得到：，再套上迹并做矩阵乘法交换：，注意这里我们根据交换了与。对照导数与微分的联系，得到。
注意：这里不能用，导数与乘常数矩阵的交换是不合法则的运算（而微分是合法的）。有些资料在计算矩阵导数时，会略过求微分这一步，这是逻辑上解释不通的。
2：，求。其中是列向量，是矩阵，是列向量，exp表示逐元素求指数，是标量。
先使用矩阵乘法、逐元素函数法则求微分：，再套上迹并做矩阵乘法/逐元素乘法交换、矩阵乘法交换：
，注意这里我们先根据交换了、与，再根据交换了与。对照导数与微分的联系，得到。
3【线性回归】：， 求的最小二乘估计，即求的零点。其中是列向量，是矩阵，是列向量，是标量。
严格来说这是标量对向量的导数，不过可以把向量看做矩阵的特例。先将向量模平方改写成向量与自身的内积：，求微分，使用矩阵乘法、转置等法则：。对照导数与微分的联系，得到。的零点即的最小二乘估计为。
4【方差的最大似然估计】：样本，求方差的最大似然估计。写成数学式是：，求的零点。其中是列向量，是样本均值，是对称正定矩阵，是标量。
首先求微分，使用矩阵乘法、行列式、逆等运算法则，第一项是，第二项是
。再给第二项套上迹做交换：
，其中先交换迹与求和，然后将 交换到左边，最后再交换迹与求和，并定义为样本方差矩阵。得到。对照导数与微分的联系，有，其零点即的最大似然估计为。
5【多元logistic回归】：，求。其中是除一个元素为1外其它元素为0的列向量，是矩阵，是列向量，是标量；，其中表示逐元素求指数，代表全1向量。
首先将softmax函数代入并写成，这里要注意逐元素log满足等式，以及满足。求微分，使用矩阵乘法、逐元素函数等法则：。再套上迹并做交换，注意可化简，这是根据等式，故。对照导数与微分的联系，得到。
另解：定义，则，先如上求出，再利用复合法则：
，得到。
最后一例留给经典的神经网络。神经网络的求导术是学术史上的重要成果，还有个专门的名字叫做BP算法，我相信如今很多人在初次推导BP算法时也会颇费一番脑筋，事实上使用矩阵求导术来推导并不复杂。为简化起见，我们推导二层神经网络的BP算法。
6【二层神经网络】：，求和。其中是除一个元素为1外其它元素为0的的列向量，是矩阵，是矩阵，是列向量，是标量；同例3，是逐元素sigmoid函数。
定义，，，则。在前例中已求出。使用复合法则，注意此处都是变量：
，使用矩阵乘法交换的迹技巧从第一项得到，从第二项得到。接下来求，继续使用复合法则，并利用矩阵乘法和逐元素乘法交换的迹技巧：
，得到。为求，再用一次复合法则：
，得到。
参考链接: https://zhuanlan.zhihu.com/p/24709748