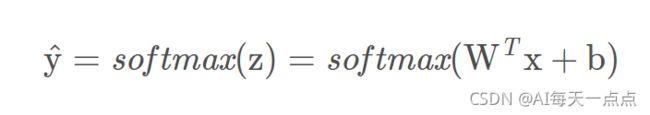CNN卷积神经网络python——计算机视觉的基石

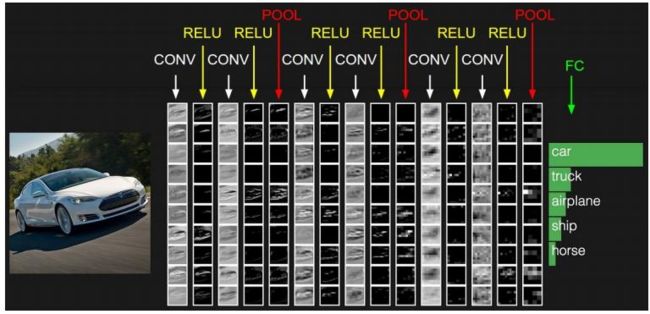
导读：神经网络接受输入图像/特征向量，并通过一系列隐藏层转换，然后使用非线性激活函数。每个隐藏层也由一组神经元组成，其中每个神经元都与前一层中的所有神经元完全连接。神经网络的最后一层（即“输出层”）也是全连接的，代表网络的最终输出分类。

Python人工智能系列学习资料获取和学习问题解答可以扫文末加V

---

CNN神经网络 

 一般卷积神经网络有如下结构：

•数据输入层/ Input layer
•卷积计算层/ CONV layer
•ReLU激励层 / ReLU layer
•池化层 / Pooling layer
•全连接层 / FC layer
当然卷积层，Relu激励层与Pooling层可以多次使用

输入层/ Input layer

该层要做的处理主要是对原始图像数据进行预处理，其中包括：

•去均值：把输入数据各个维度都中心化为0，如下图所示，其目的就是把样本的中心拉回到坐标系原点上。

•归一化：幅度归一化到同样的范围，如下所示，即减少各维度数据取值范围的差异而带来的干扰，比如，我们有两个维度的特征A和B，A范围是0到10，而B范围是0到10000，如果直接使用这两个特征是有问题的，好的做法就是归一化，即A和B的数据都变为0到1的范围。

•PCA/白化：用PCA降维；白化是对数据各个特征轴上的幅度归一化

卷积层

卷积层是卷积神经网络的核心构建块。这层参数由一组K 个可学习过滤器（即“内核”）组成，其中每个过滤器都有宽度和高度，并且几乎总是正方形。

对于 CNN 的输入，深度是图像中的通道数（即，处理 RGB 图像时深度为 3，每个通道一个）。对于网络中更深的卷积，深度将是前一层应用的过滤器数量。

为了让这个概念更清晰，让我们考虑 CNN 的前向传递，我们在输入体积的宽度和高度上对K 个滤波器中的每一个进行卷积。更简单地说，我们可以想象我们的K 个内核中的每一个都在输入区域上滑动，计算元素级乘法、求和，然后将输出值存储在二维激活图中。

 左：在 CNN 的每个卷积层，有K 个内核。中间：K 个内核中的每一个都与输入进行了卷积。右图：每个内核产生一个 2D 输出，称为激活图。卷积过程可以参考下图

在将所有K 个过滤器应用于输入体积后，我们现在有K个二维激活图。然后我们沿着阵列的深度维度堆叠我们的K 个激活图，以形成最终的输出体积。

获得K个激活图后，将它们堆叠在一起，形成网络中下一层的输入。

因此，输出中的每一个都是一个神经元的输出，它只“观察”输入的一小部分区域。通过这种方式，神经网络“学习”过滤器，当它们在输入中的给定空间位置看到特定类型的特征时激活。在网络的较低层，当过滤器看到类似边缘或类似角落的区域时，它们可能会激活。

这里有三个参数控制输出体积的大小：depth、stride和zero-padding大小

 depth

输出图像的深度。每个过滤器都会生成一个激活图，在K个内核的卷积中，激活图的深度将为K，或者只是我们在当前层中学习的过滤器的数量。

stride

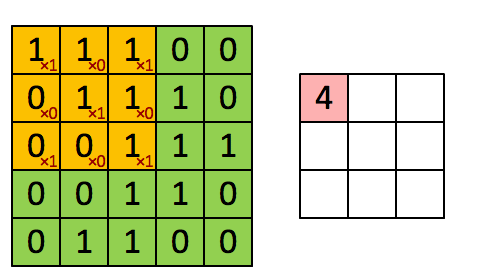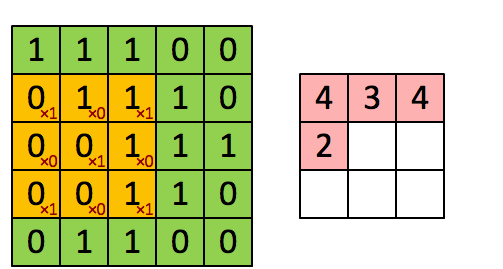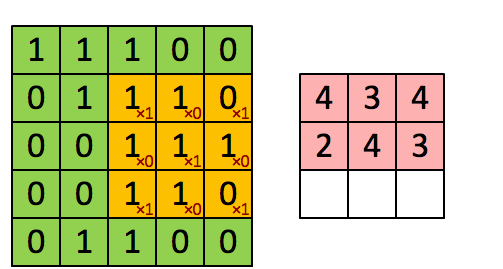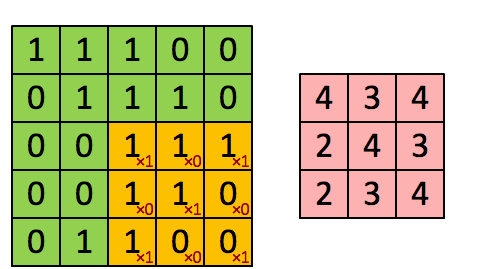
考虑我们将卷积操作描述为在大矩阵上“滑动”一个小矩阵，在每个坐标处停止，计算元素乘法求和，然后存储输出。这个描述类似于一个滑动窗口，它从左到右、从上到下在图像上滑动。这里我们有一个 5 × 5 的输入图像和一个 3 × 3 的卷积内核。

 使用S = 1，我们的内核从左到右和从上到下滑动，一次一个像素，产生以下输出（左图）。若使用S = 2的步幅，我们一次跳过两个像素（沿x轴的两个像素和沿y轴的两个像素），将会输出更少的数据量（下图）

 左： 1 × 1 步长的卷积输出。右图： 2 × 2 步长的卷积输出

zero-padding

在应用卷积时，我们需要“填充”输入图像的边界以保留经过CNN卷积后的原始图像大小。使用zero-padding，我们可以沿着边界“填充”我们的输入图像，使得我们经过CNN后输出体积大小与我们的输入体积大小完全一样。我们应用的填充量由参数P控制。

为了可视化zero-padding，我们将 3 × 3 卷积内核应用于步长为S = 1的 5 × 5 输入图像

从上图中，我们可以看到卷积后的图片尺寸为3*3，如果我们改为设置P = 1，我们可以用零填充我们的输入图片（右）以创建一个 7 × 7 的图片尺寸，然后应用卷积操作，得到5*5的输出图片，这跟输入图片的尺寸大小完全一致。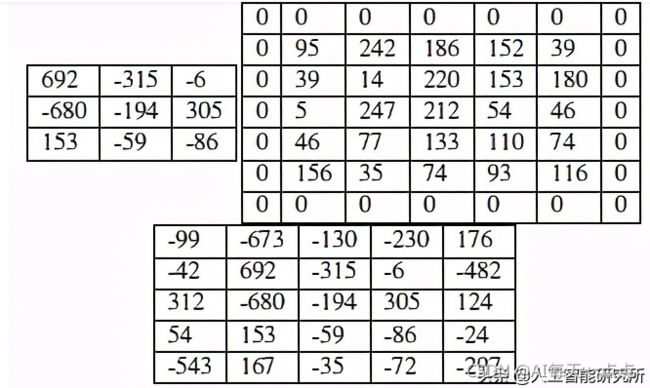

•ReLU激励层 / ReLU layer

 

左上角：阶跃函数。右上角： Sigmoid 激活函数。左中：双曲正切。中右： ReLU 激活（深度神经网络最常用的激活函数）。左下： Leaky ReLU，允许负数的 ReLU 变体。右下： ELU，ReLU 的另一种变体，其性能通常优于 Leaky ReLU。

CNN采用的激励函数一般为ReLU(The Rectified Linear Unit/修正线性单元)，它的特点是收敛快，求梯度简单，但较脆弱，图像如下。

在输入图片进行CNN卷积后，通常我们需要使用激励函数对输出的图片数据进行激励，一般神经网络最常见的是ReLU激励函数，说白一点，此函数便是当小于0的数据全部替换成0，大于0的数据是y=x，直接是输入的值

此层接受大小为W input ×H input ×D input的输入图片，然后应用给定的激活函数。由于激活函数以元素方式应用，激活层的输出始终与输入维度相同，W input = W output，H input = H output，D input = D output。

 

激活函数

池化层 / Pooling layer
有两种方法可以减小输入图片的大小，CNN 以及pooling，常见的卷积神经网络的步骤为

输入 = >CNN = > RELU = >pooling= >CNN = > RELU = >pooling = > FC

池化层夹在连续的卷积层中间， 用于压缩数据和参数的量，减小过拟合。简而言之，如果输入是图像的话，那么池化层的最主要作用就是压缩图像。池化层用的方法有Max pooling 和 average pooling，而实际用得较多的是Max pooling。

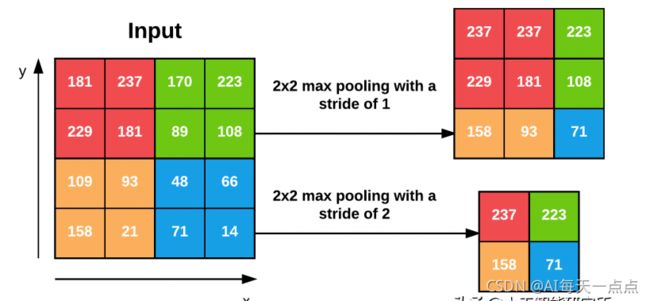
通常我们使用 2 × 2的池大小，我们还将步幅设置为S = 1 或S = 2。下图应用最大池化的示例，其中池大小为 2 × 2，步幅为S = 1。每 2 × 2 块，我们只保留最大值，从而产生 3 × 3的输出体积大小。

我们可以通过增加步幅来进一步减小输出体积的大小——这里我们将S = 2 应用于相同的输入。对于输入中的每个 2 × 2 块，我们只保留最大值，然后以两个像素为步长，再次应用该操作，我们得到2*2的输出图片大小。

全连接层

深度神经网络的最后一层往往是全连接层+Softmax（分类网络），如下图所示

全连接层将权重矩阵与输入向量相乘再加上偏置，将n个(−∞,+∞)的实数映射为K个(−∞,+∞)的实数（分数）；Softmax将K个(−∞,+∞)的实数映射为K个(0,1)的实数（概率），同时保证它们之和为1。具体如下：

其中，x为全连接层的输入，Wn*K为权重，b为偏置，y^为Softmax输出的概率，Softmax的计算方式如下：

 

dropout

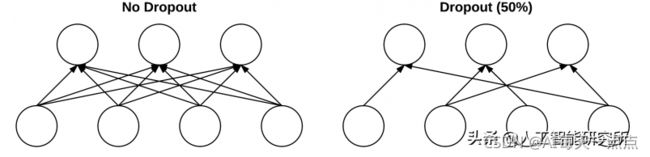
Dropout 实际上是一种正则化形式，旨在通过提高测试准确性来帮助防止过度拟合，可能会以牺牲训练准确性为代价。对于我们训练集中的每个小批量，dropout 层以概率p随机断开网络架构中从前一层到下一层的输入。

我们应用 dropout 的原因是通过在训练时,改变网络架构来减少过拟合

 

如上图：图中黑色曲线是正常模型，绿色曲线就是overfitting模型。尽管绿色曲线很精确地区分了所有的训练数据，但是并没有描述数据的整体特征，对新测试数据的适应性较差，且训练模型太复杂，后期的训练数据会很庞大。

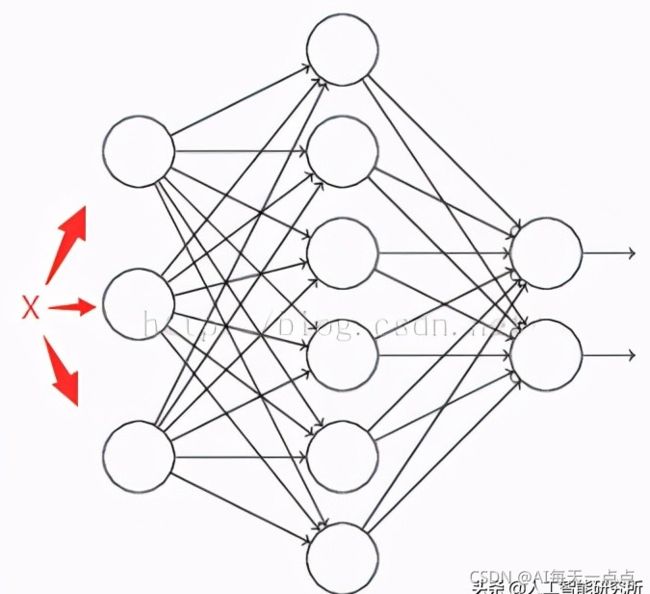
假设有一个神经网络：

按照之前的方法，根据输入X，先正向更新神经网络，得到输出值，然后反向根据backpropagation算法来更新权重和偏向。而Dropout不同的是，

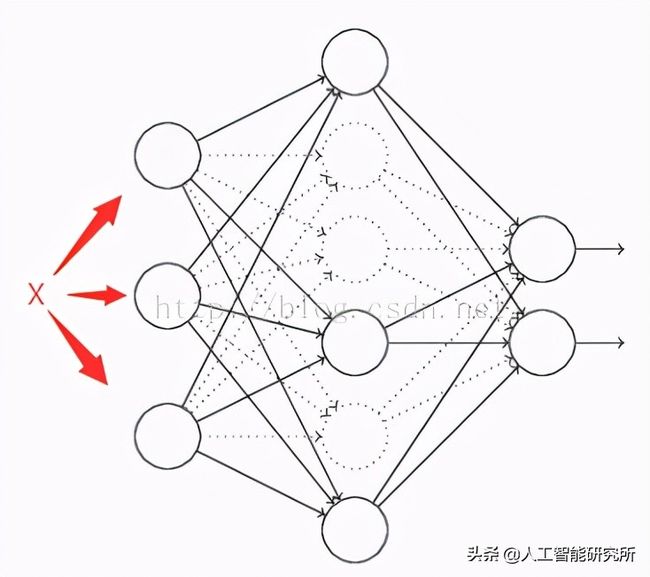
1）在开始，随机删除掉隐藏层一半的神经元，如图，虚线部分为开始时随机删除的神经元：

2）然后，在删除后的剩下一半的神经元上正向和反向更新权重和偏差；

3）再恢复之前删除的神经元，再重新随机删除一半的神经元，进行正向和反向更新w和b;

4）重复上述过程。

---

 Python人工智能系列学习资料获取和学习问题解答扫码加微（更方便）

还有200G的人工智能资源包无任何套路免费提供,也可以进人工智能技术交流群：966367816