Python机器学习--分类\回归算法--KNN(K最近邻)算法
KNN算法介绍与类型
K最近邻(K-Nearest Neighbors,KNN)算法是一种基本的分类和回归算法【有监督学习】,也是最简单易懂的机器学习算法,没有之一。1968年由Cover和Hart提出,应用场景有字符识别、文本分类、图像识别等领域。
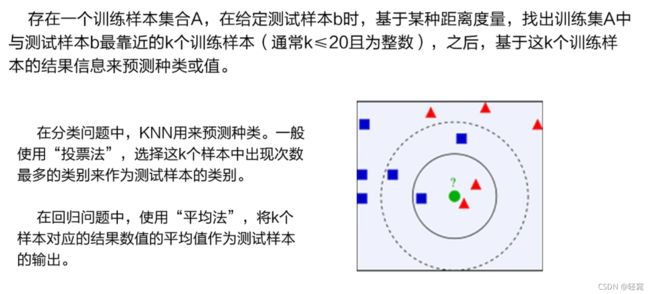
算法的思想: 一个样本与数据集中的k个样本最相似, 如果这k个样本中的大多数属于某一个类别, 则该样本也属于这个类别。
KNN算法的原理
1.计算测试样本与训练集中所有样本之间的相似度(使用距离表征相似度.)
2.按照距离递增排序
3.选择与测试样本中距离最近的k个训练样本.
4.根据选择出的K个样本的标签,进行投票或平均 (投票为分类问题,求平均为回归问题).
相似度计算
KNN算法的特点
1、惰性学习算法(边测试,边训练),没有明显的训练过程、
2、计算复杂度高(原理上最初的KNN是暴力搜索,KD树和球树都是改进算法)
- - KD树:建立树花费较多的计算时间,占空间;在搜索K个最近邻时可以降低距离的计算次数
- - 计算各个类别的质心(聚类中心),测试样本和所有质心比较相似度,排除点距离较远的某些类别
3、设置的K值不同,预测结果不同——如何选择最优的K值
交叉验证——利用嵌套循环探究k值和knn中的参数weights的最佳匹配
for k in [1, 15 , 2]:
for w in ['distance', 'uniform']:
网格搜索——网格搜索的基础就是交叉验证,是通过sklearn的方法来实现的
from sklearn.model_selection import GridSearchCV
# 实例化
# 有两个重要参数
# 1、算法名称, 比如knn
# 2、param_grid={"n_neighbors":[3,5,7,9], "weights":['uniform', 'distance']}
grid = GridSearchCV(knn, param_grid={"n_neighbors":[3,5,7,9], "weights":['uniform', 'distance']})
# 拟合
grid.fit(x_train, y_train)
print('最好的参数:', grid.best_params_)
print('最好的得分:', grid.best_score_)
KNN算法的API
def __init__(self, n_neighbors=5,
weights='uniform', algorithm='auto', leaf_size=30,
p=2, metric='minkowski', metric_params=None, n_jobs=None,
**kwargs):
参数n_neighbors ---k
参数weights权重:distance or uniform
训练集中 各个类别的 样本数量不均衡时(设置weights=distance)
超过4:1 属于不均衡
distance就是通过计算距离待测样本的距离值来确定最终的分类,uniform就是上面所一直在用的,统计数量来确定最终的分类。
参数algorithm:{'auto', 'ball_tree', 'kd_tree', 'brute'} # 默认auto
# 自动选择 球树 K维树 暴力搜索
参数:metric 距离计算的公式是谁?KNN算法优化
KD树
KD树的优化原理:
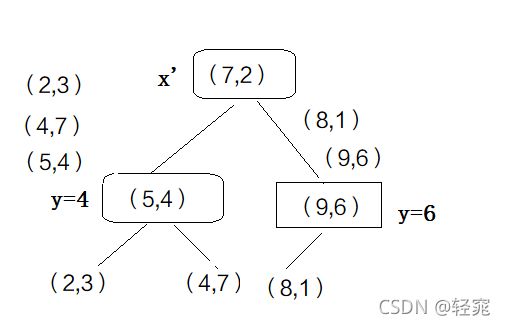
1、对于一个只有两个特征x和y的训练集,比较两列的特征的方差,方差最大的作为第一个考虑对象,将其从小到大排列,选出中位数(注意:此处的中位数必须是一个固定的值,也就是说当有两个中位数时,不需要求他们的均值,只需要任选一个),选出中位数所在的(x,y)作为根节点(比如方差最大的是x列,根节点的子节点将考虑y列的中位数,子节点的子节点再考虑x,以此类推)
2、将小于中位数的(x,y)作为根节点的左子节点,将大于中位数的(x,y)作为根节点的右子节点,再对两个子节点的y值进行排序和求中位数,比中位数小的放左边,比中位数大的放右边,直到每个子节点只剩一个叶子节点时停止
搜索方法:
1、比如给定一组特征(2.1,3.1),由于我们上面的kd树的根节点是先根据x判断的,所以先判断2.1和7的大小,很显然比7小放到根节点的左边
2、根节点的子节点是根据y来判断的,所以比较3.1和4的大小,比4小放到左边
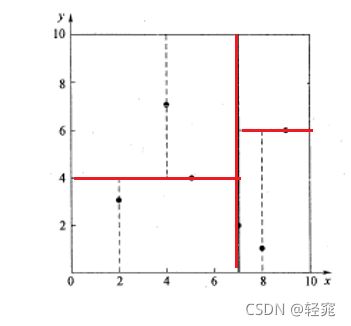
3、进行回溯(如下图所示:红线为中位数),先从路径中取出(2,3)点作为最近邻点,计算到查询点的距离,dis=0.1414。再回溯到父节点(5,4),以(2.1,3.1)为圆心,dis为半径画圆,发现并不与y=4相交,也就是说没有大于四与(2.1,3.1)更临近,所以(5,4)的右子树就不再考虑
4、继续向上回溯到根节点,同理以(2.1,3.1)为圆心,dis为半径画圆,更不会与x=7相交,所以不考虑(7,2)的右子树
5、得出结论,与(2.1,3.1)最近邻的点是(2,3)
如下图所示:在此kd树中只进行了三次运算,如果使用暴力搜索则会进行六次运算,比暴力搜索快
KD树小结
目的:减少计算次数(在所有训练样本中,寻找和测试样本最近的K个样本)
训练过程:建立树:使用训练集建立树(消耗空间和时间)
第一次计算各个特征的方差,选择方差大的特征进行划分;划分点选择该列特征的中位数(必须存在的中位数)
之后每一层的构建:轮流使用各个维度
测试过程:搜索最近的节点
使用sklearn中的KNN实现电影分类
根据不同种类镜头数量预测电影类型
# 导包
from sklearn.neighbors import KNeighborsClassifier
train_X = train_data[["搞笑镜头", "拥抱镜头", "打斗镜头"]]
# 获取训练集标签
train_y = train_data['电影类型']
# 测试集样本
test_X = ['25', '42', '12']
# 实例化knn
# n_neighbors相当于k
knn = KNeighborsClassifiter(n_neighbors=5)
# 拟合
knn.fit(train_X, train_y)
# 预测
y_pred = knn.predict(test_X)
# 获取准确率(test_y为真实测试集标签)
print('准确率:', knn.score(test_X, test_y))
KNN算法普通代码实现
import numpy as np
# 以预测电影类型作为例子,标签为离散型,所以用分类算法
# 获取训练集样本特征
train_X = train_data[["搞笑镜头", "拥抱镜头", "打斗镜头"]]
# 获取训练集标签
train_y = train_data['电影类型']
# 测试集样本
test_X = ['25', '42', '12']
# 计算相似度
dis = np.sqrt(np.sum((test_X - train_X)**2, axis=1))
# 增加一列距离列
train_data['距离'] = dis
# 对距离排序
train_data.sort_values(by='距离', inplace=True)
# 获取k=5并求众数
print('电影类型:', train_data['距离'].head(5).mode()[0])