雷达信号处理---MTI滤波器设计仿真
MTI滤波器通过合理设置频率响应中的“凹口”能够有效的抑制杂波,提高雷达信号的信杂比,有利于运动目标的检测。以地杂波为例,其杂波功率主要分布在零频以及雷达重复频率的整数倍处,那么我们只要设计一个在杂波主要分布频率点处有“凹口”的滤波器,就能很好的抑制杂波。
1.延迟线对消器
延迟线对消器是比较常用的MTI滤波器之一。这里主要介绍单延迟线对消器以及双延迟线对消器。
1)单延迟线对消器
单延迟线对消器的实现框图如下。
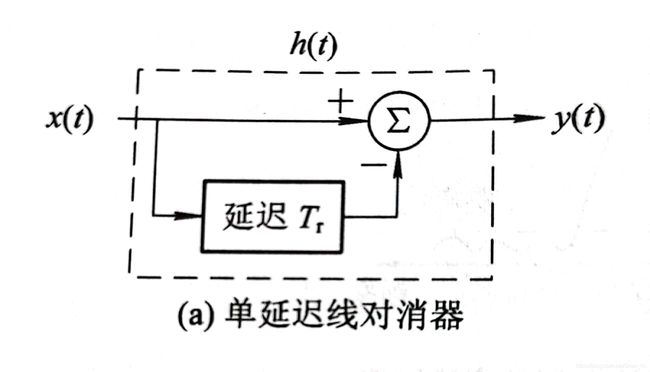
我们可由此写出输入信号与输出信号的关系
y ( t ) = x ( t ) − x ( t − T r ) y(t)=x(t)-x(t-T_{r}) y(t)=x(t)−x(t−Tr)
则滤波器的脉冲响应为
h ( t ) = δ ( t ) − δ ( t − T r ) h(t)=\delta (t)-\delta (t-T_{r}) h(t)=δ(t)−δ(t−Tr)
频率响应可写为
H ( ω ) = 1 − e − j ω T r H(\omega )=1-e^{-j\omega T_{r}} H(ω)=1−e−jωTr
根据上式,我们便可以在matlab中进行仿真验证了
2)双延迟线对消器
双延迟线对消器是由两个单延迟线对消器级联构成的,其实现框图如下
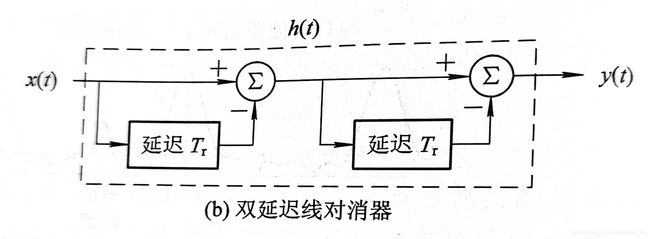
双延迟线脉冲响应可由上图得出为 h ( t ) = δ ( t ) − 2 δ ( t − T r ) + δ ( t − 2 T r ) h(t)=\delta (t)-2\delta (t-T_{r}) +\delta (t-2T_{r}) h(t)=δ(t)−2δ(t−Tr)+δ(t−2Tr)
其功率增益为
∣ H ( ω ) ∣ = ∣ H 1 ( ω ) ∣ 2 ∣ H 1 ( ω ) ∣ 2 |H(\omega )|=|H_{1}(\omega )|^{2}|H_{1}(\omega )|^{2} ∣H(ω)∣=∣H1(ω)∣2∣H1(ω)∣2
其中, ∣ H 1 ( ω ) ∣ |H_{1}(\omega )| ∣H1(ω)∣是单延迟线对消器的功率增益
同理,多延迟线对消器是由多个单延迟线对消器构成的
其实现框图如下

而经过类推发现,对消器的系数其实是二项式系数,即
ω n = ( − 1 ) n C N n = ( − 1 ) n N ! ( N − n ) ! n ! \omega _{n}=(-1)^{n}C_{N}^{n} =(-1)^{n}\frac{N!}{(N-n)!n!} ωn=(−1)nCNn=(−1)n(N−n)!n!N!
同时,通过观察其实现框图可以发现,延迟对消器是一种滤波器系数为二项式系数的特殊FIR滤波器。
3)仿真验证
现有一脉冲信号,其脉冲重复频率为 f r f_{r} fr,设计单延迟线滤波器与双延迟线滤波器
仿真结果如下

仿真代码
%%signal_canceler
fofr1=3;
eps=0.00001;
fofr=0:0.01:fofr1;
arg1=pi.*fofr;
resp=4.*((sin(arg1)).^2);
max1=max(resp);
resp=resp./max1;
subplot(3,1,1);
plot(fofr,resp,'k');
xlabel('归一化频率f/fr');
ylabel('幅度响应');
grid;
subplot(3,1,2);
resp_db=10*log10(resp+eps);
plot(fofr,resp_db,'k');
xlabel('归一化频率f/fr');
ylabel('幅度响应/dB');
grid;
%%double_canceler
resp_double=resp.*resp;
subplot(3,1,3);
plot(fofr,resp,'k',fofr,resp_double,'r');
xlabel('归一化频率f/fr');
ylabel('幅度响应');
legend('单延迟线对消器','双延迟线对消器');
grid;
可以看到对零频以及fr整数倍的信号有很好的抑制作用,同时双延迟线脉冲响应比单延迟线滤波器有更宽的“凹口”,抑制效果更好。
2.参差重复频率
但是上述的延迟对消器却有所不足,若所要探测的目标信号回波正好在脉冲重复频率的整数倍处,那么便会被滤波器抑制掉,产生“盲速”现象。
这时便需要使用参差重复频率,即采用N个重复频率,记为 [ f r 1 , f r 2 , f r 3 , . . . , f r n ] [f_{r1},f_{r2},f_{r3},...,f_{rn}] [fr1,fr2,fr3,...,frn],其脉冲重复周期为 T r 1 : T r 2 : . . . : T r N = K 1 : K 2 : . . . : K N T_{r1}:T_{r2}:...:T_{rN}=K_{1}:K_{2}:...:K_{N} Tr1:Tr2:...:TrN=K1:K2:...:KN,我们称 [ K 1 : K 2 : . . . : K N ] [K_{1}:K_{2}:...:K_{N}] [K1:K2:...:KN]为参差码,公比为 Δ T \Delta T ΔT。
若 K i K_{i} Ki之间互为素数,则MTI滤波器的第一盲速对应的多普勒频率为 1 Δ T \frac{1}{\Delta T} ΔT1(结合上文中会在脉冲重复频率处产生凹口,便不难理解)。
这里再引出一个重要参数 K a v K_{av} Kav, K a v K_{av} Kav是参差码的均值,也被称为盲速拓展倍数。若雷达平均重复周期为 T r T_{r} Tr,满足关系式 T r = 1 N ∑ N i = 1 T r i = K a v ∗ Δ T T_{r}=\frac{1}{N}\sum_{N}^{i=1}T_{ri}=K_{av}*\Delta T Tr=N1N∑i=1Tri=Kav∗ΔT则 K a v = T r Δ T = f b n f r K_{av}=\frac{T_{r}}{\Delta T}=\frac{f_{bn}}{f_{r}} Kav=ΔTTr=frfbn
参差MTI滤波器的结构如下图
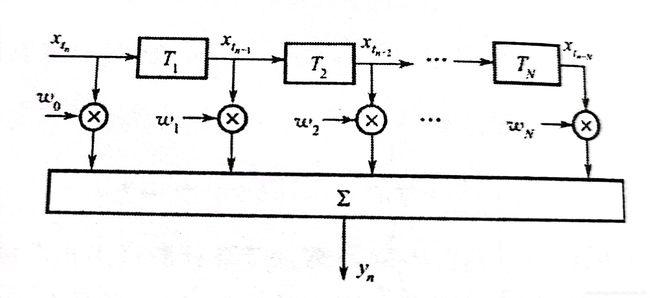
可由上图推出MTI滤波器的频率响应
H ( j ω ) = ω 0 + ω 1 e − j 2 π f T 1 + ω 2 e − j 2 π f ( T 1 + T 2 ) . . . + ω n e − j 2 π f ( ( T T 2 + . 1 + . . + T N ) H(j\omega )=\omega _{0}+\omega _{1}e^{-j2\pi fT_{1}}+\omega _{2}e^{-j2\pi f(T_{1}+T_{2})}...+\omega _{n}e^{-j2\pi f((T_{T_{2}+.1}+..+T_{N})} H(jω)=ω0+ω1e−j2πfT1+ω2e−j2πf(T1+T2)...+ωne−j2πf((TT2+.1+..+TN)
此时,若 [ ω 0 , ω 1 , ω 2 , . . . , ω n ] [\omega _{0} ,\omega _{1}, \omega _{2},...,\omega _{n}] [ω0,ω1,ω2,...,ωn]为二项式系数,就构成了参差对消器。
仿真实验
仿真参差比分别为[27:28:29]、[28:29:27]、[29:27:28]的三脉冲参差对消器

仿真代码
function [w]=ceni_MTI(len,bianT,f)%len为参差码长度 bianT为参差码 f为滤波器频率范围
fr=1/mean(bianT);%计算平均重复频率 mean计算平均值
bianT_num=length(bianT);
bianT=repmat(bianT,1,len);%重复数组 bianT=[27 28 29 27 28 29 27 28 29] 此处是为了方便计算三组参差码27:28:29 ,28:29:27,29:27:28
T=zeros(1,len);
f_ran=f.*fr;%频率范围
hd=zeros(bianT_num,length(f));%频率响应
N=len-1;
for m=0:N%计算二项式系数
w(m+1)=(-1)^(m-1)*factorial(N)/(factorial(m)*factorial(N-m));
end
for k=1:bianT_num
for m=2:len
T(m)=sum(bianT(k:k+m-2));
end
hd(k,:)=w*exp(-j*2*pi*T'*f_ran);
end
Hd=20*log10(abs(hd));
figure;plot(f_ran./fr,Hd);
xlabel('归一化频率');ylabel('幅度响应/dB');
legend('27:28:29','28:29:27','29:27:28');
axis([0 28 -40 40]);
3.优化MTI滤波器—特征矢量法
在之前的MTI滤波器设计中,我们取滤波器的系数为二项式系数,用于抑制杂波。现在,我们的目标是寻找新的一组滤波器系数,用于更有效的抑制杂波。
特征矢量法是其中的一种方法,以改善因子最大为准则。
首先我们列出N个脉冲的杂波的自相关矩阵 R c R_{c} Rc表达式
R c = [ r c ( 0 , 0 ) r c ( 0 , 1 ) . . . r c ( 0 , N − 1 ) r c ( 1 , 0 ) r c ( 1 , 1 ) . . . r c ( 1 , N − 1 ) . . . . . . . . . . . . r c ( N − 1 , 0 ) r c ( N − 1 , 1 ) . . . r c ( N − 1 , N − 1 ) ] R_{c}=\begin{bmatrix} r_{c}(0,0) & r_{c}(0,1) & ... &r_{c}(0,N-1) \\ r_{c}(1,0) & r_{c}(1,1) & ... &r_{c}(1,N-1) \\ ... & ... &... & ...\\ r_{c}(N-1,0) & r_{c}(N-1,1) &... &r_{c}(N-1,N-1) \end{bmatrix} Rc=⎣⎢⎢⎡rc(0,0)rc(1,0)...rc(N−1,0)rc(0,1)rc(1,1)...rc(N−1,1)............rc(0,N−1)rc(1,N−1)...rc(N−1,N−1)⎦⎥⎥⎤
其中, r c ( m , n ) = e − 2 π 2 σ f 2 τ m n 2 e j 2 π f 0 τ m n r_{c}(m,n)=e^{-2\pi ^{2}\sigma _{f}^{2}\tau _{mn}^{2}}e^{j2\pi f_{0}\tau _{mn}} rc(m,n)=e−2π2σf2τmn2ej2πf0τmn
谱中心为 f 0 f_{0} f0,谱宽为 σ f \sigma _{f} σf, τ m n = t m − t n \tau _{mn}=t_ {m}-t_{n} τmn=tm−tn为相关时间
其次,我们再列出改善因子与相关矩阵的关系式(具体过程不推导)
I = S o / C o S i / C i = ω H ω ω H R c ω I=\frac{S_{o}/C_{o}}{S_{i}/C_{i}}=\frac{\omega^{H}\omega }{\omega^{H}R_{c}\omega } I=Si/CiSo/Co=ωHRcωωHω
其中, ω \omega ω为滤波器的权系数
R c R_{c} Rc的特征方程为 R c ω n = λ n ω n R_{c}\omega_{n}=\lambda_{n}\omega_{n} Rcωn=λnωn,其中
λ 0 ≤ λ 1 ≤ . . . ≤ λ n \lambda_{0}\leq \lambda_{1 }\leq ...\leq\lambda_{n} λ0≤λ1≤...≤λn
在 R c R_{c} Rc的特征值中,大特征值对应的特征向量张成的子空间为信号子空间,小特征值对应的特征向量张成的子空间为噪声子空间,杂波主要分布于信号子空间。而噪声子空间与信号子空间是正交的!那么,若是我们取最小特征值 λ 0 \lambda_{0} λ0的特征向量为MTI滤波器的加权系数,不就能极大的抑制杂波,使改善因子最大了吗?
仿真验证
得出以上结论后,我们做仿真验证
假设重复频率为100Hz,参差比为27:28:29,地杂波中心频率为0Hz,谱宽为0.64Hz,设计一单凹口的四脉冲对消器。

仿真代码
function [ww]=eig_MTI(firjie,fr,bianT,fd,df)
%firjieMTI滤波器长度 fr脉冲平均重复频率 bianT变T码 fd杂波谱中心 df杂波谱宽
bianT=bianT/fr/mean(bianT);
bianT_num=length(bianT);
bianT=repmat(bianT,1,firjie);
T=zeros(1,firjie);
f=[-fr:0.1:fr*4];%杂波频率范围
hd=zeros(bianT_num,length(f));
Rc=zeros(firjie,firjie);%杂波自相关矩阵
for k=1:bianT_num
for m=2:firjie
T(m)=sum(bianT(k:k+m-2));
end
for m=1:firjie
% Rc(m,:)=exp(((fd+1i*2*pi*df^2*(T(m)-T)).^2-fd^2)/(2*df.^2));
Rc(m,:)=exp(-2*pi^2*df^2*(T(m)-T).^2+1i*2*pi*fd*(T(m)-T));
end
[V,D]=eig(Rc);%eig 求特征值D,特征向量V
w=V(:,1);
ww(k,:)=w;
end
hd=ww*exp(-1i*2*pi*T'*f);
Hd=20*log10(abs(hd));
figure;
plot(f./fr,Hd);
xlabel('归一化频率f/fr');
ylabel('幅度响应/dB');
grid;
legend('27:28:29','28:29:27','29:28:27');