概率论与数理统计(Probability & Statistics II)

---

概率论与数理统计(Probability & Statistics I)
概率论与数理统计(Probability & Statistics II)

---

样本与抽样分布(Sample and Sampling Distribution)

数理统计(Statistics)

数理统计是以概率论为基础, 关于实验数据的收集、整理、分析与推断的一门科学与艺术。

总体(population)：研究对象的全体；
个体(individual)：总体中的每一个具体对象称为个体；
总体的容量(capacity)：总体中包含的个体数；
有限总体(finite population)：容量有限的总体；
无限总体(infinite population)：容量无限的总体。通常将容量非常大的有限总体也按无限总体处理。

为了采用数理统计方法进行分析，首先要收集数据，数据收集方法一般有两种。
（1）通过调查、记录收集数据。（2）通过实验收集数据。

实际中人们通常只关注总体的某个（或几个）指标。

• 总体的某个指标$X$, 对于不同的个体来说有不同的取值, 这些取值构成一个分布, 因此$X$可以看成一个随机变量。
• 有时候直接将$X$称为总体. 假设$X$的分布函数为$F(x)$, 也称$X$服从$F(x)$分布$X\sim F(x)$

如何推断总体分布的未知参数（或分布）？
需要从总体中抽取一部分个体, 根据这部分个体的数据，并利用概率论的知识等作出分析推断.被抽取的部分个体叫做总体的一个样本(sample)。

简单随机样本(simple random sample)：满足以下两个条件的随机样本 $(X_1,X_2,\dots ,X_n)$ 称为容量是$n$的简单随机样本，简称样本。
(1) 代表性：每个$X_i$与$X$同分布；
(2) 独立性：$(X_1,X_2,\dots ,X_n)$是相互独立的随机变量。

获得简单随机样本的抽样称为简单随机抽样。

• 对于有限总体，采用放回抽样.
• 但当总体容量很大的时候，放回抽样有时候很不方便， 因此在实际中当总体容量比较大时，通常将不放回抽样所得到的样本近似当作简单随机样本来处理.
• 对于无限总体， 一般采取不放回抽样.

对样本 $X_1,X_2,\dots ,X_n$ 进行观测后，得到的数值：$x_1,x_2,\dots ,x_n$ 称为样本观测值(observed value)
观测前：$X_1,X_2,\dots ,X_n$ 是随机变量
观测后：$x_1,x_2,\dots ,x_n$ 是具体的数据

样本的联合分布：设总体 $X\sim F(x)$，则样本 $X_1,X_2,\dots ,X_n$ 的联合分布函数为：$F(x_1,x_2,\dots ,x_n)=P\{X_1⩽x_1,\dots ,X_n⩽x_n\}=\prod _{i=1}^{n}F(x_i)$
若总体 $X$ 的密度函数为 $f(x)$，则样本 $X_1,X_2,\dots ,X_n$ 的联合密度函数为：$f(x_1,x_2,\dots ,x_n)=\prod _{i=1}^{n}f(x_i)$
若总体 $X$ 的分布律为 $P\{X=a_k\}=p_k$，则样本 $X_1,X_2,\dots ,X_n$ 的联合分布律为：$P\{X_1=x_1,\dots ,X_n=x_n\}=\prod _{i=1}^{n}P\{X=x_i\}$

抽样分布(Sampling distribution)

从样本中提取有用的信息来研究总体的分布及各种特征数——构造统计量.
统计量(statistic)：设 $X_1,X_2,\dots ,X_n$ 是来自总体$X\sim F(x)$ 的样本， $g(x_1,x_2,\dots ,x_n)$ 是$n$元实值连续函数，若函数$g(x_1,x_2,\dots ,x_n)$ 不含未知参数， 则称随机变量 $g(X_1,X_2,\dots ,X_n)$ 为统计量。
常用统计量
(1) 样本均值：$\bar{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$
(2) 样本方差：$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\bar{X}{)}^2$
样本标准差：$S=\sqrt{S^2}$
(3) 样本 k 阶原点矩：$A_k=\frac{1}{n}\sum _{i=1}^n{X}_i^k$
样本 k 阶中心矩：$B_k=\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^k$
(4) 将样本按由小到大的顺序排成 $X_{(1)}⩽X_{(2)}⩽\dots ⩽X_{(n)}$
顺序统计量(order statistic)： $X_{(1)},X_{(2)},\dots ,X_{(n)}$
样本极小值(minimum)：$X_{(1)}=\min \{X_{(1)},X_{(2)},\dots ,X_{(n)}\}$
样本极大值(maximum)：$X_{(n)}=\max \{X_{(1)},X_{(2)},\dots ,X_{(n)}\}$
样本极差(range)：$R_n=X_{(n)}-X_{(1)}$

样本均值与样本方差的数字特征：设$X_1,X_2,\dots ,X_n$ 是来总体 $X$ 的样本，且总体的均值与方差存在，记为$E(X)=\mu ,D(X)={\sigma }^2$，则有
(1) $E(\bar{X})=E(\frac{1}{n}\sum _{i=1}^n{X}_i)=\frac{1}{n}\sum _{i=1}^{n}E(X_i)=\mu$
$D(\bar{X})=D(\frac{1}{n}\sum _{i=1}^n{X}_i)=\frac{1}{n^2}\sum _{i=1}^{n}D(X_i)={\sigma }^2/n$
(2) $E(S^2)={\sigma }^2$
(3) 若 $X\sim N(\mu ,{\sigma }^2)$，则 $D(S^2)=\frac{2{\sigma }^4}{n-1}$

抽样分布(sampling distribution)：统计量的分布被称为抽样分布
当总体$X$服从一般分布（如指数分布、均匀分布等），要得出统计量的分布是很困难的。当总体$X$服从正态分布时，统计量 $\bar{X},S^2$是可以计算的，本节主要介绍与标准正态总体相关的抽样分布。

${\chi }^2$ 分布(chi-square distribution)：设 $X_1,X_2,\dots ,X_n$ 相互独立，且都服从标准正态分布 $N(0,1)$ ，则称随机变量 $${\chi }^2=\sum _{i=1}^n{X}_i^2$$ 服从自由度为 $n$ 的 ${\chi }^2$ 分布，记为 ${\chi }^2\sim {\chi }^2(n)$，自由度指包含的独立变量的个数。
${\chi }^2$ 分布的概率密度为：$$f_n(x)=\{\begin{array}{l}\frac{1}{2\Gamma (n/2)}(\frac{x}{2}{)}^{n/2-1}{e}^{-x/2},x>0\\ 0,x⩽0\end{array}$$ 其中 $\Gamma (x)={\int }_0^{+\infty }{t}^{x-1}{e}^{-t}\mathrm{d}t$

性质：
(1) 设 $Y\sim {\chi }^2(n)$，则 $E(Y)=n,D(Y)=2n$
(2) 分布的可加性：设 $Y_1\sim {\chi }^2(n_1),Y_2\sim {\chi }^2(n_2)$，且$Y_1,Y_2$相互独立，则 $Y_1+Y_2\sim {\chi }^2(n_1+n_2)$
推广：设$Y_1,Y_2,\cdots ,Y_m$相互独立，且 $Y_i\sim {\chi }^2(n_i)$，则 $\sum _{i=1}^m{Y}_i\sim {\chi }^2(\sum _{i=1}^m{n}_i)$

t 分布(t-distribution)：设 $X\sim N(0,1),Y\sim {\chi }^2(n)$，且 X与 Y 相互独立，则称随机变量$$T=\frac{X}{\sqrt{Y/n}}$$服从自由度为 n 的 t 分布，记为 $T\sim t(n)$
$t(n)$分布的概率密度为：$$f_n(x)=\frac{\Gamma (\frac{n+1}{2})}{\sqrt{n\pi }\Gamma (\frac{n}{2})}(1+\frac{x^2}{n}{)}^{-\frac{n+1}{2}},x\in \mathbb{R}$$
特别地，$n=1$ 的 t 分布就是柯西分布 $f(x)=\frac{1}{\pi (1+x^2)},x\in \mathbb{R}$
$\underset{n\to \infty }{\lim }{f}_n(x)=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2},x\in \mathbb{R}$

F 分布(F-distribution)：设 $X\sim {\chi }^2(n_1),Y\sim {\chi }^2(n_2)$，且 X与 Y 相互独立，则称随机变量$$F=\frac{X/n_1}{Y/n_2}$$服从自由度为 $(n_1,n_2)$ 的 F 分布，记为 $F\sim F(n_1,n_2)$，其中 $n_1$称为第一自由度, $n_2$称为第二自由度。
$F(n_1,n_2)$分布的概率密度为：$$f(x)=\{\begin{array}{l}\frac{(n_1/n_2{)}^{\frac{n_1}{2}}}{B(\frac{n_1}{2},\frac{n_2}{2})}{x}^{\frac{n_1}{2}-1}(1+\frac{n_1}{n_2}x{)}^{-\frac{n_1+n_2}{2}},x>0\\ 0,x⩽0\end{array}$$其中 $B(a,b)={\int }_0^1{x}^{a-1}(1-x{)}^{b-1}\mathrm{d}x=\frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}$

重要性质：若 $F\sim F(n_1,n_2)$，则$\frac{1}{F}\sim F(n_2,n_1)$

正态总体的抽样分布
设 $X_1,X_2,\dots ,X_n$ 是来自正态总体 $N(\mu ,{\sigma }^2)$的样本，样本均值$\bar{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$，样本方差$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\bar{X}{)}^2$，则
(1) $\bar{X}\sim N(\mu ,{\sigma }^2/n)$
(2) $\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$
(3) $\bar{X}$与 $S^2$相互独立
(4) $\frac{\bar{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$

设 $X_1,X_2,\dots ,X_{n_1}$和$Y_1,Y_2,\dots ,Y_{n_2}$ 分别来自正态总体 $N({\mu }_1,{\sigma }_1^2)$和$N({\mu }_2,{\sigma }_2^2)$的样本，均值分别为 $\bar{X},\bar{Y}$，方差分别为$S_1^2,S_2^2$，则
(1) $\frac{S_1^2/S_2^2}{{\sigma }_1^2/{\sigma }_2^2}\sim F(n_1-1,n_2-1)$

(2) $\frac{(\bar{X}-\bar{Y})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}\sim N(0,1)$
(3) 当 ${\sigma }_1^2={\sigma }_2^2={\sigma }^2$时

$\frac{(\bar{X}-\bar{Y})-({\mu }_1-{\mu }_2)}{S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\sim t(n_1+n_2-2)$
其中 $S_w^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2},S_w=\sqrt{S_w^2}$

参数估计(Parameter Estimation)

参数通常是刻画总体某些概率特征的数量。例如正态分布 $N(\mu ,{\sigma }^2)$ 中的参数 $\mu$ 就是该分布的均值，参数 σ2 是该分布的方差。当该参数未知时，从总体中抽取一个样本，用某种方法对该未知参数进行估计，这就是参数估计。
参数估计的形式：先从该总体中抽样得到样本，然后构造样本函数，求出未知参数的估计值或取值范围，这就是点估计和区间估计。

假设总体 $X\sim F(x;{\theta }_1,{\theta }_2,\dots ,{\theta }_m)$，其中分布函数 $F$ 的表达式已知，但参数 ${\theta }_1,{\theta }_2,\dots ,{\theta }_m$ 未知，若记 $\theta =({\theta }_1,{\theta }_2,\dots ,{\theta }_m)$，则总体分布可记为 $X\sim F(x;\theta )$，参数 $\theta$ 的取值范围称为参数空间(parameter space)，记为 $\Theta$

点估计(Point estimation)

$X_1,X_2,\dots ,X_n$ 是来自总体 $X\sim F(x;{\theta }_1,{\theta }_2,\dots ,{\theta }_m)$的一个样本，${\theta }_1,{\theta }_2,\dots ,{\theta }_m$ 是未知参数，构造 m 个统计量：
$随机变量\{\begin{array}{l}{\hat{\theta }}_1(X_1,X_2,\dots ,X_n)\\ {\hat{\theta }}_2(X_1,X_2,\dots ,X_n)\\ ⋮\\ {\hat{\theta }}_m(X_1,X_2,\dots ,X_n)\end{array}$
把样本观测值 $x_1,x_2,\dots ,x_n$ 代入上统计量，就得到 m 个数值：
$数值\{\begin{array}{l}{\hat{\theta }}_1(x_1,x_2,\dots ,x_n)\\ {\hat{\theta }}_2(x_1,x_2,\dots ,x_n)\\ ⋮\\ {\hat{\theta }}_m(x_1,x_2,\dots ,x_n)\end{array}$
称 ${\hat{\theta }}_k(X_1,X_2,\dots ,X_n)$为 ${\theta }_k$的估计量(estimate)，${\hat{\theta }}_1(x_1,x_2,\dots ,x_n)$为${\theta }_k$的估计值(estimator)。

常用的估计方法：矩估计法，极大似然估计法，最小二乘估计法，贝叶斯方法

矩估计法(Moment Estimation)
矩估计思想：以样本矩估计总体矩，以样本矩的函数估计总体矩的函数。
由辛钦大数定律，有 $A_k=\frac{1}{n}\sum _{i=1}^n{X}_i^k\stackrel{P}{}{\mu }_k({\theta }_1,{\theta }_2,\dots ,{\theta }_m)(n\to \infty )$
因此当n较大时有 $A_k\approx {\mu }_k({\theta }_1,{\theta }_2,\dots ,{\theta }_m)$假设总体的前m阶矩存在，令$A_k={\mu }_k({\theta }_1,{\theta }_2,\dots ,{\theta }_m),k=1,2,\cdots ,m$得方程组，其解 ${\hat{\theta }}_k(X_1,X_2,\dots ,X_n)$ 称为 ${\theta }_k$的矩估计量。

总体均值和方差的矩估计量表达式不因不同的总体分布而异，设总体$X$的均值 $\mu$及方差${\sigma }^2$都存在
$\hat{\mu }=\bar{X},{\hat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2\triangleq {\tilde{S}}^2$
设总体$X\sim U(a,b)⟹\hat{a}=\bar{X}-\sqrt{3}\tilde{S},\hat{b}=\bar{X}+\sqrt{3}\tilde{S}$

极大似然估计法(Maximum Likelihood Estimate,MLE)
Fisher的极大似然思想：
假设总体 $X$ 是离散型随机变量，其分布律为 $P\{X=x\}=p(x;\theta ),\theta \in \Theta$，θ未知，$X_1,X_2,\dots ,X_n$为样本，其观察值为 $x_1,x_2,\dots ,x_n$，则事件 $\{X_1=x_1,X_2=x_2,\cdots ,X_n=x_n\}$发生的概率（联合分布律）为$$L(\theta )=L(x_1,x_2,\dots ,x_n;\theta )=\prod _{i=1}^{n}p(x_i;\theta ),\theta \in \Theta$$这一概率随θ的取值而改变，我们自然的认为使概率取得最大值的θ值较为合理，$L(\theta )$称为样本的似然函数(likelihood function)，方程$$L(\hat{\theta })=\underset{\theta \in \Theta }{\max }L(\theta ),\hat{\theta }=\hat{\theta }(x_1,x_2,\dots ,x_n)$$的解 $\hat{\theta }$称为极大似然估计值，统计量 $\hat{\theta }=\hat{\theta }(X_1,X_2,\dots ,X_n)$为θ 的极大似然估计量(MLE)
连续型随机变量 $X$的概率密度函数为 $f(x;\theta ),\theta \in \Theta$，可取得似然函数为$$L(\theta )=L(x_1,x_2,\dots ,x_n;\theta )=\prod _{i=1}^{n}f(x_i;\theta ),\theta \in \Theta$$

在许多情况下，$p(x;\theta ),f(x;\theta )$关于θ可微，这时 $\hat{\theta }$常可从方程 $\frac{\mathrm{d}}{\mathrm{d}\theta }L(\theta )=0$解得，又因 $L(\theta )$和 $\ln L(\theta )$在同一处取得极值，因此$\hat{\theta }$也可从方程$$\frac{\mathrm{d}}{\mathrm{d}\theta }\ln L(\theta )=0$$求得，这一方程被称作对数似然方程。
极大似然估计法同样适用于分布中含多个参数 ${\theta }_1,{\theta }_2,\dots ,{\theta }_m$的情况，这时似然函数L是这些未知参数的函数，分别令 $\frac{\partial }{\partial {\theta }_i}L=0,i=1,2,\cdots ,m$或$$\frac{\partial }{\partial {\theta }_i}\ln L=0,i=1,2,\cdots ,m$$解上述由m个方程组成的方程组即可，上式称为对数似然方程组。
设总体$X\sim N(\mu ,{\sigma }^2)⟹\hat{\mu }=\bar{X},{\hat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2\triangleq {\tilde{S}}^2$
设总体$X\sim U(a,b)⟹\hat{a}=\min \{X_1,X_2,\cdots ,X_n\}=X_{(1)},\hat{b}=\max \{X_1,X_2,\cdots ,X_n\}=X_{(n)}$

极大似然估计的不变性：设 $\hat{\theta }$是$\theta$的极大似然估计，θ 的函数 $u=u(\theta )$且有单值反函数 $\theta =\theta (u)$，则 $u(\hat{\theta })$是 $u$ 的极大似然估计。

估计量的评判标准(Criteria for estimators)

对同一个参数，不同方法得到的估计量可能不同。用什么标准来评价一个估计量的好坏?
(1) 无偏性(unbiased)：设$X_1,X_2,\dots ,X_n$为总体 $X\sim F(x;\theta )(\theta \in \Theta )$ 的样本，若参数 $\theta$ 的估计量 $\hat{\theta }=\hat{\theta }(X_1,X_2,\dots ,X_n)$满足 $E(\hat{\theta })=\theta$，则$\hat{\theta }$是 $\theta$的一个无偏估计量。
若$E(\hat{\theta })\ne \theta$，则 $|E(\hat{\theta })-\theta |$称为估计量 $\theta$ 的偏差。
若$\underset{n\to \infty }{\lim }E(\hat{\theta })=\theta$，则称$\hat{\theta }$是 $\theta$的渐近无偏估计量

估计量$\hat{\theta }(X_1,X_2,\dots ,X_n)$是随机变量，而估计值会有波动性，无偏性的统计意义是指在大量重复试验下，保证了没有系统误差。

设$X_1,X_2,\dots ,X_n$是总体 $X$ 的样本，总体的k阶矩为${\mu }_k$，期望和方差为$\mu ,{\sigma }^2$
$E(A_k)={\mu }_k$，样本 k阶矩都是总体k阶矩的无偏估计
特别的，$E(\bar{X})=\mu ,E(S^2)={\sigma }^2$
而 $E({\tilde{S}}^2)=\frac{n-1}{n}E(S^2)=\frac{n-1}{n}{\sigma }^2$不是总体方差的无偏估计
$\underset{n\to \infty }{\lim }E({\tilde{S}}^2)={\sigma }^2$，${\tilde{S}}^2$是方差的渐进无偏估计。

纠偏方法：若$\hat{\theta }$是有偏估计，$E(\hat{\theta })=a\theta +b(a\ne 0,\theta \in \Theta )$，则$\frac{\theta -b}{a}$是θ 的无偏估计，上面就是用了此方法。

(2) 有效性(effective)：设 ${\hat{\theta }}_1,{\hat{\theta }}_2$ 都是 θ 的无偏估计量，若有 $\forall \theta \in \Theta ,D({\hat{\theta }}_1)⩽D({\hat{\theta }}_2)$，且不等号至少对某一 $\theta \in \Theta$ 成立，则 ${\hat{\theta }}_1$比 ${\hat{\theta }}_1$ 有效。

均方误差准则：定义$E(\hat{\theta }-\theta {)}^2$是估计量 $\hat{\theta }$的均方误差(mean square error;MSE)，记作$Mse(\hat{\theta })$，若$\hat{\theta }$是θ 的无偏估计量，则 $Mse(\hat{\theta })=D(\hat{\theta })$。
设设 ${\hat{\theta }}_1,{\hat{\theta }}_2$ 都是 θ的点估计，若有 $\forall \theta \in \Theta ,Mse({\hat{\theta }}_1)⩽Mse({\hat{\theta }}_2)$，且不等号至少对某一 $\theta \in \Theta$ 成立，则在均方误差条件下 ${\hat{\theta }}_1$优于 ${\hat{\theta }}_1$ 。
在实际应用中,均方误差准则比无偏性准则更重要

(3) 相合性(consistence)：设$\hat{\theta }(X_1,X_2,\dots ,X_n)$是参数θ的估计量
若$\forall \theta \in \Theta ,\forall ϵ>0,\underset{n\to \infty }{\lim }P\{|\hat{\theta }-\theta |<ϵ\}=1$
即 ${\hat{\theta }}_n\stackrel{P}{}\theta (n\to \infty )$，称$\hat{\theta }$为θ的相合估计量。

相合性的相关结论：
(1) 样本 k 阶矩$A_k$是总体 k 阶矩 ${\mu }_k$ 的相合估计量；-----辛钦大数定律证明
(2) $S^2,{\tilde{S}}^2$是总体方差的相合估计量。-----切比雪夫不等式证明
(3) 矩估计量一般是相合估计量。

应用
(1) 设 $X\sim N(\mu ,{\sigma }^2)⟹Mse(S^2)=D(S^2)=\frac{2{\sigma }^4}{n-1},Mse({\tilde{S}}^2)=\frac{2n-1}{n^2}{\sigma }^4$
当 $n>1$时，$Mse(S^2)>Mse({\tilde{S}}^2)$因此在均方误差条件下${\tilde{S}}^2$优于$S^2$

(2) 设$X_1,X_2,\dots ,X_n$是总体指数分布$X\sim Exp(\theta )$的样本
θ 的矩估计量$\bar{X}$和极大似然估计量 $nZ,Z=\min \{X_1,X_2,\dots ,X_n\}$均是无偏估计；
但 $D(\bar{X})={\theta }^2/n,D(nZ)={\theta }^2$，当 $n>1$时，$D(\bar{X})<D(nZ)$，所以$\bar{X}$比 $nZ$有效；

区间估计(Interval estimation)

对于一个未知量，根据具体样本观测值，点估计提供一个明确的数值。还希望根据所给的样本确定一个随机区间， 使其包含参数真值的概率达到指定的要求。

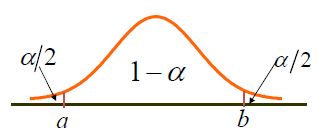
置信区间(Confidence Intervals)：设总体 $X\sim F(x;\theta ),\theta \in \Theta$，若对
给定的$\alpha (0<\alpha <1)$，由来自 $X$的样本确定的两个统计量 ${\hat{\theta }}_L={\hat{\theta }}_L(X_1,X_2,\dots ,X_n),{\hat{\theta }}_U={\hat{\theta }}_U(X_1,X_2,\dots ,X_n)({\hat{\theta }}_L<{\hat{\theta }}_U)$，对于$\forall \theta \in \Theta$，满足$$P\{{\hat{\theta }}_L<\theta <{\hat{\theta }}_U\}⩾1-\alpha$$则称随机区间$({\hat{\theta }}_L,{\hat{\theta }}_U)$为θ的置信度为 $1-\alpha$ 的置信区间(confidence interval)。${\hat{\theta }}_L,{\hat{\theta }}_U$分别称为置信下限和置信上限， $1-\alpha$称为置信度或置信水平(confidence level)。
说明：
(1) 参数θ虽然未知，但是确定的值。置信区间$({\hat{\theta }}_L,{\hat{\theta }}_U)$是随机的，依赖于样本，样本不同，算出的区间也不同。对于有些样本观察值，区间覆盖θ，但对于另一些样本观察值，区间则不能覆盖。反复抽样多次(各次样本容量相同)，按伯努利大数定律，在这些区间中，包含真值的比例约为 $1-\alpha$
(2) 相同的置信水平也可以得到不同的区间估计。称置信区间$({\hat{\theta }}_L,{\hat{\theta }}_U)$的平均长度$E({\hat{\theta }}_U-{\hat{\theta }}_L)$为区间的精确度(accuracy)（长度最短，精度最高），精确度的一半为误差限(error limit)。在给定的样本容量下，置信水平和精确度是相互制约的。
(3) Neyman原则：在置信水平达到$1-\alpha$的置信区间中，选精确度尽可能高的置信区间。

求解置信区间的一般方法
(1) 构造样本的一个函数 $G=G(X_1,X_2,\dots ,X_n;\theta )$它含有待估参数θ，不含其它未知参数，其分布已知，且分布不依赖于待估参数（常由θ的点估计出发考虑），具有这种性质的函数称为枢轴量(pivot)。
(2) 对于给定的置信水平$1-\alpha$，求出两个分位点$a,b$，使得 $P\{a<G<b\}⩾1-\alpha$
(3) 由 $a<G<b$得到与之等价的θ不等式 ${\hat{\theta }}_L<\theta <{\hat{\theta }}_U$，那么$({\hat{\theta }}_L,{\hat{\theta }}_U)$就是置信度为 $1-\alpha$ 的置信区间。
分位点(percentile point)：设连续型随机变量 $X$的概率密度函数为 $f(x)$，对给定的 $\alpha (0<\alpha <1)$，称满足条件 $P\{X>x_{\alpha }\}={\int }_{x_{\alpha }}^{\infty }f(x)\mathrm{d}x=\alpha$ 的点 $x_{\alpha }$为 α 分位点。
标准正态分布 $N(0,1)$的α 分位点记作 $z_{\alpha },z_{\alpha }=-z_{1-\alpha }$
${\chi }^2(n)$分布的α 分位点记作 ${\chi }_{\alpha }^2(n)$
$t(n)$分布的α 分位点记作 $t_{\alpha }(n),t_{\alpha }(n)=-t_{1-\alpha }(n)$
$F(n_1,n_2)$分布的α 分位点记作 $F_{\alpha }(n_1,n_2)$

单侧置信区间(one-sided confidence interval)
如果$P\{{\hat{\theta }}_L<\theta \}⩾1-\alpha$则称随机变量${\hat{\theta }}_L$为θ的置信度为 $1-\alpha$ 的单侧置信下限(one-side confidence lower limit)。
如果$P\{\theta <{\hat{\theta }}_U\}⩾1-\alpha$则称随机变量${\hat{\theta }}_U$为θ的置信度为 $1-\alpha$ 的单侧置信上限(two-side confidence lower limit)。

正态总体参数的区间估计示例
设总体 $X\sim N(\mu ,{\sigma }^2),X_1,X_2,\dots ,X_n$为样本，$\bar{X},S^2$分别为样本均值和样本方差，置信区间为 $1-\alpha$
(1) ${\sigma }^2$已知时，$\bar{X}$是 μ 的极大似然估计，取枢轴量 $G=\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$
设常数 $a,b$满足： $P\{a<G<b\}⩾1-\alpha$
等价于$P\{\bar{X}-\frac{\sigma }{\sqrt{n}}b<\mu <\bar{X}-\frac{\sigma }{\sqrt{n}}a\}⩾1-\alpha$
此时区间的长度为 $(b-a)\sigma /\sqrt{n}$

由正态分布的对称性知，$a=-b=-z_{\alpha /2}$时，区间的长度达到最短 $L=z_{\alpha /2}\sigma /\sqrt{n}$
n固定，置信水平提高，即$1-\alpha$增大，则 $z_{\alpha /2}$增大，所以 $L$ 变大，精确度降低；反之亦然.
所得 μ 双侧置信区间为 $(\bar{X}-\frac{\sigma }{\sqrt{n}}{z}_{\alpha /2},\bar{X}+\frac{\sigma }{\sqrt{n}}{z}_{\alpha /2})$
单侧置信下限为 $\bar{X}-\frac{\sigma }{\sqrt{n}}{z}_{\alpha }$
单侧置信上限为 $\bar{X}+\frac{\sigma }{\sqrt{n}}{z}_{\alpha }$
(2) ${\sigma }^2$已知时，以$S^2$估计${\sigma }^2$，的枢轴量 $G=\frac{\bar{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$
所得 μ 双侧置信区间为$(\bar{X}-\frac{S}{\sqrt{n}}{t}_{\alpha /2}(n-1),\bar{X}+\frac{S}{\sqrt{n}}{t}_{\alpha /2}(n-1))$
单侧置信下限为 $\bar{X}-\frac{\sigma }{\sqrt{n}}{t}_{\alpha }(n-1)$
单侧置信上限为 $\bar{X}+\frac{\sigma }{\sqrt{n}}{t}_{\alpha }(n-1)$
(3) 其他总体均值的区间估计
当n足够大时（一般 n>30），由中心极限定理知，近似 $\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$

正态总体的均值、方差的置信区间和单侧置信限（置信水平为 $1-\alpha$）

一个正态总体

待估参数	其他参数	枢轴量G的分布	置信区间	单侧置信上/下限
$\mu$	${\sigma }^2$已知	$\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$	$(\bar{X}\pm \frac{\sigma }{\sqrt{n}}{z}_{\alpha /2})$	$\bar{X}\pm \frac{\sigma }{\sqrt{n}}{z}_{\alpha /2}$
$\mu$	${\sigma }^2$未知	$\frac{\bar{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$	$\left(\bar{X}\pm \frac{S}{\sqrt{n}}{t}_{\alpha /2}(n-1)\right)$	$\bar{X}\pm \frac{\sigma }{\sqrt{n}}{t}_{\alpha }(n-1)$
${\sigma }^2$	$\mu$未知	$\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$	$\left(\frac{(n-1)S^2}{{\chi }_{\alpha /2}^2(n-1)},\frac{(n-1)S^2}{{\chi }_{1-\alpha /2}^2(n-1)}\right)$	$\frac{(n-1)S^2}{{\chi }_{\alpha /2}^2(n-1)}$ $\frac{(n-1)S^2}{{\chi }_{1-\alpha /2}^2(n-1)}$

两个正态总体

待估参数	其他参数	枢轴量G的分布	置信区间	单侧置信上/下限
${\mu }_1-{\mu }_2$	${\sigma }_1^2,{\sigma }_2^2$ 已知	$\frac{(\bar{X}-\bar{Y})-({\mu }_1-{\mu }_2)}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}\sim N(0,1)$	$\left((\bar{X}-\bar{Y})\pm z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}\right)$	$(\bar{X}-\bar{Y})\pm z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}$
${\mu }_1-{\mu }_2$	${\sigma }_1^2={\sigma }_2^2={\sigma }^2$ 未知	$\frac{(\bar{X}-\bar{Y})-({\mu }_1-{\mu }_2)}{S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\sim t(n_1$