手撕力扣之动态规划:爬楼梯、不同路径、最小路径和、三角形最小路径和、买卖股票的最佳时机、打家劫舍1和2、最小花费爬楼梯、礼物的最大价值、剪绳子、连续子数组的最大和、乘积最大子数组、单词拆分、最大正方形
力扣070.爬楼梯
class Solution {
public:
int climbStairs(int n) {
if(n == 1){return 1;}
if(n == 2){return 2;}
int a = 1, b = 2, temp;
for(int i = 3; i <= n; i++){
temp = a;
a = b;
b = temp + b;
}
return b;
}
};
力扣062.不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
class Solution {
public:
int uniquePaths(int m, int n) {
int arr[m][n];
// 第0列 和 第0行为边界 全为1
for(int i=0;i<m;i++){arr[i][0]=1;}
for(int i=0;i<n;i++){arr[0][i]=1;}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
// 动态规划表达式
arr[i][j] = arr[i-1][j] + arr[i][j-1];
}
}
return arr[m-1][n-1];
};
作者:wang-xiao-shuai-ve
链接:https://leetcode-cn.com/problems/unique-paths/solution/bu-tong-lu-jing-dong-tai-gui-hua-yu-shu-xue-by-wan/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
};
作者:carlsun-2
链接:https://leetcode-cn.com/problems/unique-paths/solution/62-bu-tong-lu-jing-shen-sou-dong-gui-shu-n7d1/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣064.最小路径和(状态压缩后)
第一行:
dp[i] = grid[0][i] + dp[i - 1];
设想我们从第二行开始,每一行的每一个点都可以由上边的点向下移动经过。
对于第i行第j列的点(i > 1)逐行遍历至该点时,有两种情况
(1)对于每行的第一个点只有他上边的点向下移动才可以经过该点
(2)剩下的点都可以由他上边的点向下移动或左边的点向右移动到达
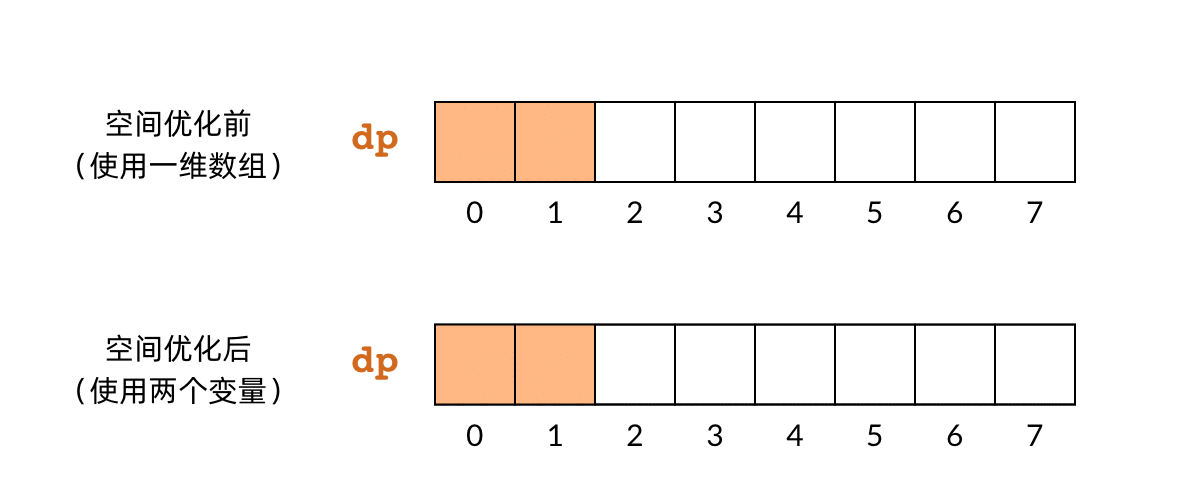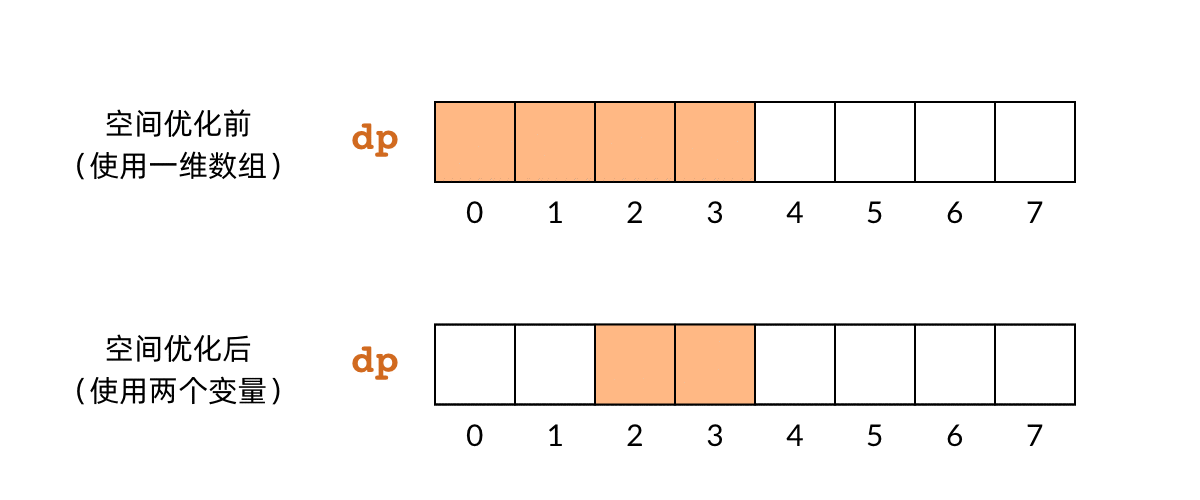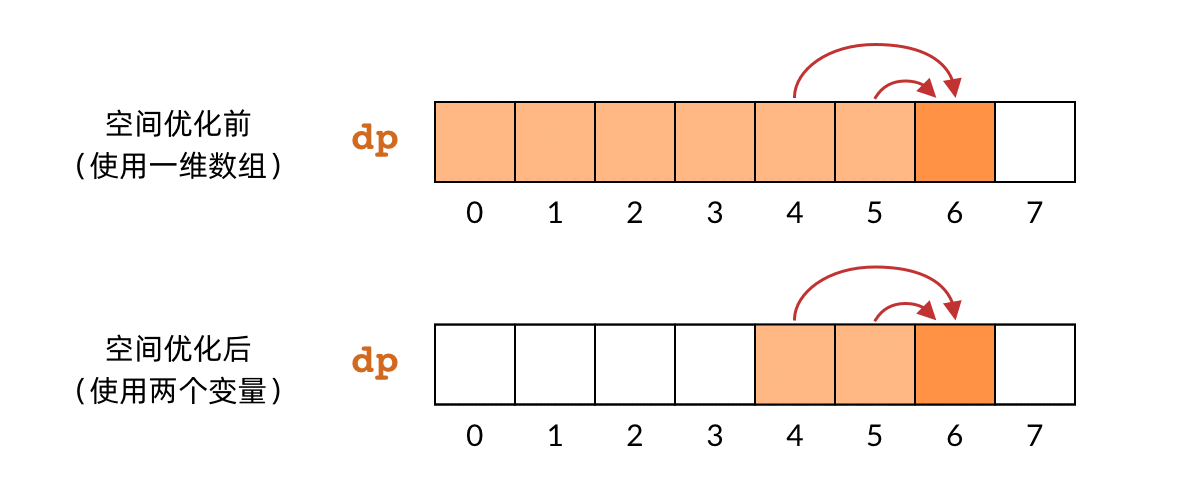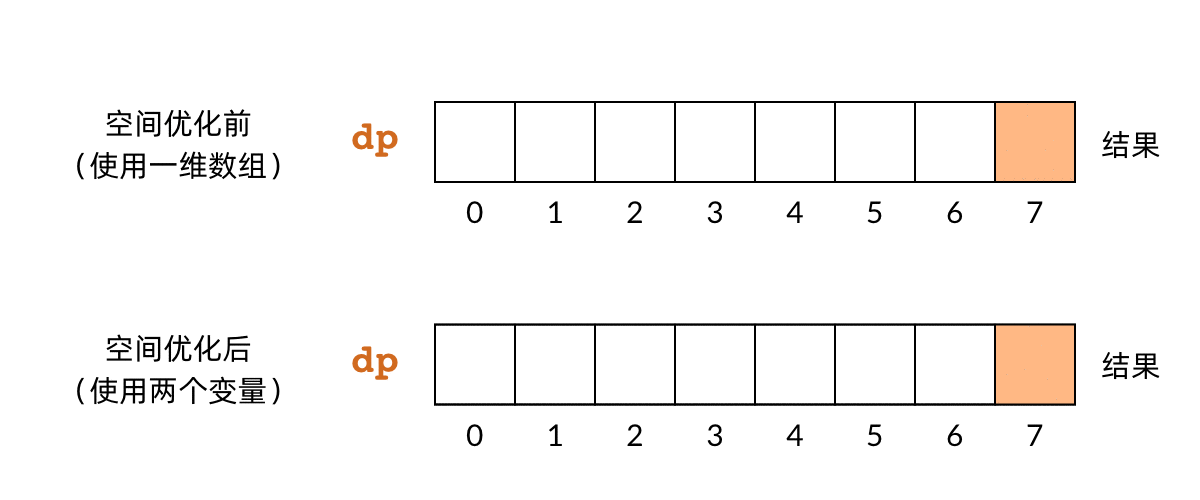
对于第一类点,我们遍历到新一行时,由于该点只能由其他点向下移动到达我们就可以根据前一行的dp[0]来更新该点的决策值
dp[0] += grid[i][0]
对于第二类点,我们可以得到如下等式
dp[j] = grid[i][j] + min(dp[j-1],dp[j])
等式右边dp[j]代表当前点上一行对应位置点的决策收益值
dp[j-1]代表当前位置左侧点的决策收益值。
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int rows = grid.size();
int cols = grid[0].size();
vector<int> dp(cols, grid[0][0]);
for (int i = 1; i < cols; ++i)
dp[i] = grid[0][i] + dp[i - 1];
for (int i = 1; i < rows; ++i) {
dp[0] += grid[i][0];
for (int j = 1; j < cols; ++j) {
dp[j] = grid[i][j] + min(dp[j], dp[j - 1]);
}
}
return dp[cols-1];
}
};
作者:6hC2sRv3gQ
链接:https://leetcode-cn.com/problems/minimum-path-sum/solution/64zui-xiao-lu-jing-he-dong-tai-gui-hua-by-6hc2srv3/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣120. 三角形最小路径和
DP自下向上(二位数组)
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
// 行数
int n = triangle.size();
// 从倒数第二行开始
for (int i = n - 2; i >= 0; i--)
{
for (int j = 0; j < triangle[i].size(); j++)
triangle[i][j] += min(triangle[i + 1][j], triangle[i + 1][j + 1]);
}
return triangle[0][0];
}
};
作者:Sunny_SMILE
链接:https://leetcode-cn.com/problems/triangle/solution/120-san-jiao-xing-zui-xiao-lu-jing-he-dpzi-shang-d/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
DP自下到上——一维数组(空间压缩)
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int n = triangle.size();
// 一维数组dp记录遍历到每一行的每个节点的最小路径和
vector<int> dp(n + 1, 0);
// 从最后一行开始依次更新每一行的dp值
for(int i = n - 1; i >= 0; i--)
for(int j = 0; j< triangle[i].size(); j++)
dp[j] = triangle[i][j] + min(dp[j],dp[j+1]);
return dp[0];
}
};
作者:Sunny_SMILE
链接:https://leetcode-cn.com/problems/triangle/solution/120-san-jiao-xing-zui-xiao-lu-jing-he-dpzi-shang-d/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣121.买卖股票的最佳时机
dp三部曲:
1.记录【今天之前买入的最小值】
2.计算【今天之前最小值买入,今天卖出的获利】,也即【今天卖出的最大获利】
3.比较【每天的最大获利】,取最大值即可
class Solution {
public:
int maxProfit(vector<int>& prices) {
if(prices.size()<=1) return 0;
int minPrice=prices[0];
int maxPro=0;
for(int i=0;i<prices.size();i++)
{
minPrice=min(minPrice,prices[i]);
maxPro=max(maxPro,prices[i]-minPrice);
}
return maxPro;
}
};
力扣198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
f[k]的意义是前i个房子中能偷到的最大金额,前3个的方案肯定包括了前2个;而 f(k) = max(f(k-1) , max( f(0), f(1), f(2), … f(k-2)) + nums[i]) ,f[k] 的意思更倾向于: 选择第k个房子的话,所能达到的最大值。
int rob(vector<int>& nums) {
if (nums.size() == 0) {
return 0;
}
// 子问题:
// f(k) = 偷 [0..k) 房间中的最大金额
// f(0) = 0
// f(1) = nums[0]
// f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }
int N = nums.size();
vector<int> dp(N+1, 0);
dp[0] = 0;
dp[1] = nums[0];
for (int k = 2; k <= N; k++) {
dp[k] = max(dp[k-1], nums[k-1] + dp[k-2]);
}
return dp[N];
}
作者:nettee
链接:https://leetcode-cn.com/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
int rob(vector<int>& nums) {
int prev = 0;
int curr = 0;
// 每次循环,计算“偷到当前房子为止的最大金额”
for (int i : nums) {
// 循环开始时,curr 表示 dp[k-1],prev 表示 dp[k-2]
// dp[k] = max{ dp[k-1], dp[k-2] + i }
int temp = max(curr, prev + i);
prev = curr;
curr = temp;
// 循环结束时,curr 表示 dp[k],prev 表示 dp[k-1]
}
return curr;
}
作者:nettee
链接:https://leetcode-cn.com/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
class Solution {
public:
int robRange(vector<int>& nums, int start, int end) {
int first = nums[start], second = max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
int temp = second;
second = max(first + nums[i], second);
first = temp;
}
return second;
}
int rob(vector<int>& nums) {
int length = nums.size();
if (length == 1) {
return nums[0];
} else if (length == 2) {
return max(nums[0], nums[1]);
}
return max(robRange(nums, 0, length - 2), robRange(nums, 1, length - 1));
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/house-robber-ii/solution/da-jia-jie-she-ii-by-leetcode-solution-bwja/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size());
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.size(); i++) {
dp[i] = min(dp[i - 2], dp[i - 1]) + cost[i];
}
return min(dp[cost.size() - 2], dp[cost.size() - 1]);
}
};
作者:armeria-program
链接:https://leetcode-cn.com/problems/min-cost-climbing-stairs/solution/yi-bu-yi-bu-tui-dao-dong-tai-gui-hua-de-duo-chong-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
状态压缩,并注意到初始值dp[0] = cost[0],dp[1] = cost[1],可以直接复用cost数组来代表dp数组。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
for (int i = 2; i < cost.size(); i++) {
cost[i] = min(cost[i - 2], cost[i - 1]) + cost[i];
}
return min(cost[cost.size() - 2], cost[cost.size() - 1]);
}
};
作者:armeria-program
链接:https://leetcode-cn.com/problems/min-cost-climbing-stairs/solution/yi-bu-yi-bu-tui-dao-dong-tai-gui-hua-de-duo-chong-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣剑指 Offer 47. 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int n = grid[0].size(), m = grid.size();
vector<int> dp(m+1, 0);
for(int j = 1; j<=n; ++j)
for(int i = 1; i<=m; ++i)
dp[i] = max(dp[i], dp[i-1]) +grid[i-1][j-1];
return dp[m];
}
};
力扣剑指 Offer 14- I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
class Solution {
public:
int cuttingRope(int n) {
// n<=3的情况,m>1必须要分段,例如:3必须分成1、2;1、1、1 ,n=3最大分段乘积是2, 同理2的最大乘积为1
if (n == 2)
return 1;
if (n == 3)
return 2;
vector<int> dp(n+1);
/*
下面3行是n>=4的情况,跟n<=3不同,4可以分很多段,比如分成1、3,
这里的3可以不需要再分了,因为3分段最大才2,不分就是3。记录最大的。
*/
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
for(int i = 4; i <= n; i++) {
int maxValue = 0;//记录最大的
//j<=i/2是因为1*3和3*1是一样的,没必要计算在内,只要计算到1*3和2*2就好了
for(int j = 1; j <= i/2; j++) {
maxValue = max(maxValue, dp[j] * dp[i-j]);
}
dp[i] = maxValue;
}
return dp[n];
}
};
力扣剑指 Offer 42. 连续子数组的最大和
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int maxnum = nums[0];
for (int i = 1;i< nums.size();++i){
if (nums[i - 1] > 0){
nums[i] += nums[i - 1];
}
maxnum = max(maxnum,nums[i]);
}
return maxnum;
}
};
作者:z1m
链接:https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/solution/dong-tai-gui-hua-by-ml-zimingmeng-2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
if(n == 0){
return 0;
} else if(n == 1) {
return nums[0];
}
int p = nums[0];
int maxP = nums[0];
int minP = nums[0];
for(int i = 1; i < n; i++) {
int t = maxP;
maxP = max(max(maxP * nums[i], nums[i]), minP *nums[i]);
minP = min(min(t * nums[i], nums[i]), minP * nums[i]);
p = max(maxP, p);
}
return p;
}
};
作者:spicy_onion
链接:https://leetcode-cn.com/problems/maximum-product-subarray/solution/dpfang-fa-xiang-jie-by-yang-cong-12/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
力扣139. 单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
【笔记】动态规划。dp[i]表示字符串s的前i个字符能否拆分成wordDict。
bool wordBreak(string s, vector<string>& wordDict) {
vector<bool> dp(s.size()+1, false);
unordered_set<string> m(wordDict.begin(), wordDict.end());
dp[0] = true;
for (int i = 1; i <= s.size(); ++i){
for (int j = 0; j < i; ++j){
if (dp[j] && m.find(s.substr(j, i-j)) != m.end()){
dp[i] = true;
break;
}
}
}
return dp[s.size()];
}
力扣221. 最大正方形
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
我们用 dp(i, j)表示以 (i,j) 为右下角,且只包含 1 的正方形的边长最大值。
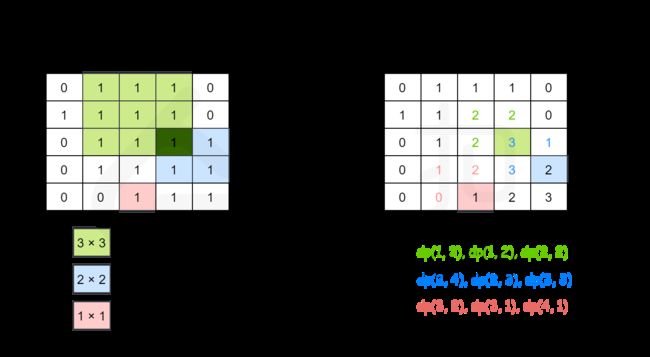
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return 0;
}
int maxSide = 0;
int rows = matrix.size(), columns = matrix[0].size();
vector<vector<int>> dp(rows, vector<int>(columns));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
maxSide = max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/maximal-square/solution/zui-da-zheng-fang-xing-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。