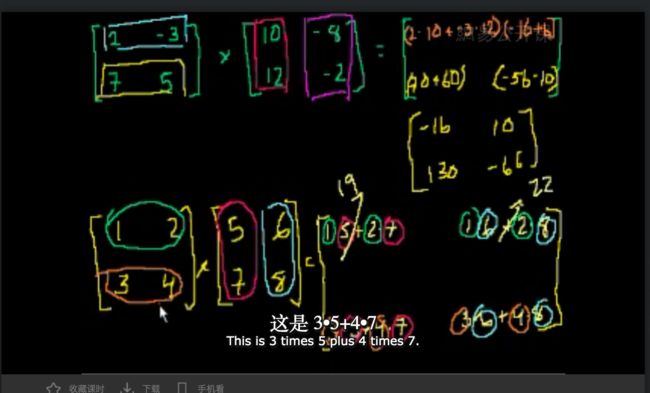https://open.163.com/movie/2011/6/D/K/M82ICR1D9_M83C881DK.html
什么是矩阵?就是数组
矩阵的加法减法
- 直接对应位置做加减法
矩阵的乘法
- 3 times 6 plus 4 times 8
AB 和 BA 乘积不相同如何理解呢
行向量* 列向量
什么是乘积
矩阵的除法 逆矩阵、矩阵的逆
单位矩阵 、方矩
A * 1/A = 1(单位矩阵)
22矩阵的逆
23矩阵的逆
矩阵的行列式、矩阵的余子式、求A的逆矩阵
矩阵法求解方程组
可以用来解二元二次方程组,把方程组转化为矩阵,逆矩阵的重要性
矩阵法求向量组合
向量组合被转化为方程组
撕开问题的面纱,发现他们是同一类问题。找到求解的新方法。
奇异矩阵
A矩阵的行列式为0的时候,没有逆矩阵。
高斯消去法
用于计算逆矩阵
向量
向量的加法、减法、乘法在坐标系中有什么体现
加、减法就是向量组成的三角形,收尾相连的两条向量相加等于第三条向量。
用向量集表示 一条直线。
三维空间 如何表示一个点,一条线,一个面?
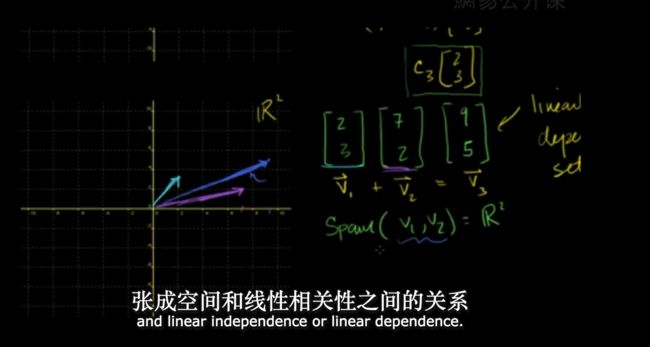
线性组合 和 向量的span张成空间
线性相关 和线性无关
二维空间的向量集合,线性无关的可以span一个二维空间
线性相关在二维空间意味着什么? 其中一个向量,可有由其他向量组合标示出来,也就是他们的和是0(他们的系数至少有一个不为0)。
线性无关在二维空间意味着什么?存在张成。
R2 至少2个向量组成张成空间????
R3 至少3个向量组成张成空间????? 2个可以张成一个R3空间么?
线性子空间
- 0在该集合内
- 向量元素*t的结果还在该集合内
- 集合内向量相加的结果还在集合内
线性代数——子空间的基
子空间的基——张成+线性无关
a basis for a set→a minimum set of vectors that spans the subspace
向量的点积和模长
向量的长度 的平方 等于该向量的点积(||A||平方 = A*A)
点积和乘积的区别
乘积,用于矩阵相乘,表示为C=A*B,A的列数与B的行数必须相同,C也是矩阵,C的行数等于A的行数,C的列数等于B的列数。Cij为A的第i行与B的第j列的点积
点积,用于向量相乘,表示为C=A*B,A与B均为向量,C为标量,也称标量积、内积、数量积等。
向量的夹角
||A|| * ||B|| > = (A* B)
A*B = ||A|| * ||B|| Cos$
R3中由点与法向量定义的平面
根据法向量 和 该平面其中一个点 ,求R3空间该平面的表达方式
外积
???外积公式只能用在 R3空间???
外积可以得到AB的非零正交向量,也就是他们平面的法向量
dot product 点积 的结果是scale 标量
乘积
cross product 外积的结果是 新的向量
外积与夹角正弦值的关系
R3空间中 向量外积 = 向量长度相乘 * 夹角正弦值
点积和外积的比较
两个向量的外积是 这两个向量组成的平行四边形的面积
矩阵行简化阶梯型 增广矩阵
用于处理多维矩阵。
??有个问题:在多维空间时,矩阵 和 向量 两个领域的交集在哪里???
????矩阵可以转化为向量运算么??????
只有0 = 0 ,并且存在自由向量时,才存在无数个解
矩阵向量积
列向量的转置,变成了行向量,也就是矩阵的形式,所有矩阵用的乘积,本质上还是向量的点积,将矩阵中行向量逆转置为原始的列向量,变成向量相乘。好奇妙。原来矩阵乘法和 向量积是这样的关系
矩阵零空间计算 the null space of A
求矩阵的最简式可以通过消元法。增广矩阵。将增广矩阵转化为行简化阶梯形
计算矩阵的零空间的方式,零空间,N(A) = SPAN([x1,x2,x3] [x1,x2,x3]) ,N(A) * A = 0`向量。A的零空间就是 A向量*B向量 = 0向量,B向量的集合就是A的零空间。
计算方式。
矩阵乘以向量是0向量 --> 增广矩阵 --> 行简化阶梯形 ---> 将N元一次等式转化为张成空间的表达方式?
算是学习了一种新方法,如何将N元一次等式转化为张成空间的表达方式?必须过哪些点?这些点组成的张成空间,就是表达式对应的空间
零空间3-零空间与线性无关的关系
A* B = 0是线性无关的必要条件是 只有B向量为0时,等式才成立,所有要求A肯定是个无任何自由项,也就是从左上角到右下角为1,其他都为0的矩阵。
如果A的零空间是0向量,说明A的行简化阶梯形是无自由变量的。比如只有对角线位置是1。
矩阵存在自由变量时,会有很多解
矩阵的列空间
就是 把矩阵的每一列看成一个向量,向量组成的空间,或者向量组成的Span()张成空间,属于自己的另一种表达方式
零空间与列空间
自由变量 和 主变量。存在自由变量代表有很多解
矩阵 的列空间
如何理解矩阵?矩阵和空间的关系?给出了一个新角度,也就是转化为列空间,由每一列组、成一个向量,有N列,怎对应N个向量,最后矩阵组成的空间就是Sapn(N),同时可以对Span(N)求证是否线性无关、线性有关的话可以去除哪些向量(尝试去掉多余的向量)?求空间的基底。这样来看待问题。
矩阵是空间么?是一个什么样的空间?矩阵的生成空间是啥?
列空间 矩阵的生成空间
证明任意子空间基底数目相同
dimension 维度
零空间的维数或零度
零空间的维数也叫零度。零度等于A空间行简化梯度性中自由列的个数,A空间的维数是主列的个数。两个正好是互补的。零度的计算方式是,求出零空间(NullSpace)。
列空间的维数或秩
主元、主列、基底、非主列、线性独立就是线性无关的意思
Dim(C(A)) A的列空间的维数
基底列和主列的关系
基底列 和 主列个数保持一致
证明候选基底确实张成C(A)空间
行简化梯度中的基底
函数的深入理解
定义域 值域 上域
向量值函数
实数函数 或者 标量函数
线性变换
满足线性的两个条件。1、满足分配率 2、满足乘系数不变。如果存在升次则属于非线性。N元N次方程。
矩阵向量乘法与线性变换
矩阵向量乘法 是满足 线性变换的
单位矩阵
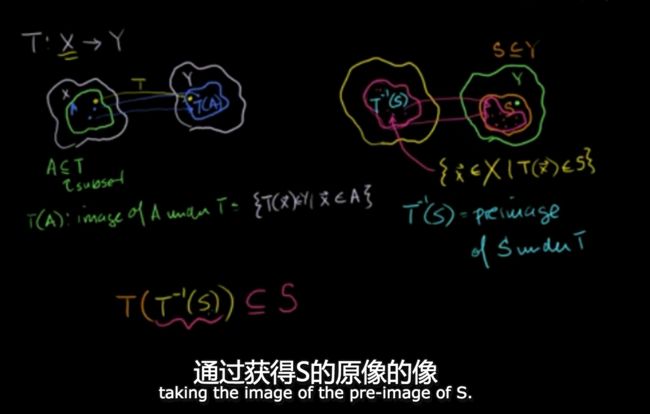
集合的像 和 原像
T(A)的像是 im(A)
T(逆-1)[A]
原像和核kernel的相关例子
有时候可以把转换T就看做是 那个矩阵(线性变换都可以重写为 一个矩阵*向量,向量是变量)。ker(T) = N(A) A就是那个矩阵空向量
线性变换的矩阵加法运算和标量运算
加深了对 线性变换的理解,一个矩阵向量 。 T(x) = Ax。或者直接看成T = A即可。T就是那个矩阵,所以就有了 T(x) + S(x) = (T+S)x
线性变换的例子——放缩和映射
例子中是能直接得到最终T的。如果思路是,把过程包含2部分,每部分对应一个T、S,就变成了T(S(x))。如何合并T\S为一个线性变换方程呢?
变换相加S+T,在空间中意味这啥?
分两种情况:变换相加 和 向量相加。T(x1+x2) 和 (T + S)(x1)
在R2空间下利用2阶矩阵表示旋转变换
反向求A矩阵时,可以借助矩阵的每一列的基向量。神奇。就这样旋转。借助基向量。也就是单位矩阵的每一列
Rot(角度):R2 --> R2
在R3空间内做旋转
绕X轴旋转、绕Y、绕Z,分别对应三个转换完成3D的操作
单位向量
长度永远是1的向量
投影介绍
projection x向量在v向量上的投影
投影到直线的矩阵向量积表示
投影到直接的转化式子是如何 改写为 线性组合(也就是矩阵向量积的方式)。思路都是借助非线性组合的表达式,通过对单位矩阵中每列基向量做转化,最终求得矩阵的方式得到的。
线性变换的复合
T(S(x))复合后的也满足线性变换
完全是人为的创造了一个概念。矩阵相乘就是线性变换的复合
矩阵乘积范例
复合被定义了一个新的名字就是 A*B (矩阵相乘)
但是计算好麻烦
矩阵乘法结合律
ABCD = A(BC)D
矩阵乘法分配率
(A+B)C = AC + BC
逆函数 可逆性和f(x)=y解唯一性等价的证明
先确定是否有可逆性
f逆(f(x)) = I(x)
恒等函数
因为是线性的 所以存在 唯一解
满射函数和单射函数
满射(映上onto函数) 就是上域等于值域
单射(one-by-one)就是 1对1的映射
映上和一对一和可逆性的联系
***可逆函数的上域和值域必须一致么?****
增广矩阵的解存在三种情况,1. 无解,也就是最后一行全是零但是结果不为零 2.只有当为0时,才有唯一的解,也就是无自由项,全都是主列时 3.有自由项存在很多非0解,是线性相关的
基向量
逆函数必须满足两个条件。1、映上 2、一对一
一个变换是映上的判别方法
如果T是一个onto满射到Rm空间,那么T的rank秩必须是m,也就是T的基向量个数必须是m个,自由向量。T的矩阵张成的空间必须是Rm。
求Ax=b的解集 72 (没有看懂)
视频里只说了,A的零空间不为0零向量的情况,也就是A矩阵无法张成该空间。如果是0向量呢?如果可以张成一个空间呢?
齐次方程式就是求Ax= 0 。
非齐次方程式 Ax= b,是非齐次方程
矩阵进行1-1变换的条件 73(没有看懂)
特解是什么?
关于可逆性的简化条件
A的行列简化式必须是一个 单位方阵
证明逆矩阵是线性变换
是线性变换就能写成 A*x向量的形式
逆矩阵的表达形式是
如何求出逆矩阵
矩阵可逆的条件
可逆的条件是A满足(简化后增广矩阵是个单位方阵)
1、映上。如何保证映上?
2、一对一。如何保证1对1?
(不太理解的地方)什么是可逆?为什么要满足以上条件?或者满足了有什么好处?
如何求出逆矩阵
A*A(-1) = I(单位方阵)
# 寻求逆矩阵的求得方法
[ A | I ] A变为I ,I变成的结果就是A'。