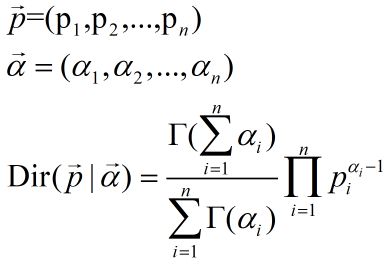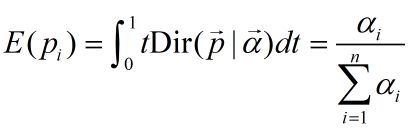- PyTorch中Tensor(张量)数据结构内部观察
科学禅道
PyTorch研究和研发范式:预训练和微调pytorch人工智能python深度学习
上图中是一个张量embeds,打开其内部存储空间,我们可以看到内部的构成。1.PyTorch中张量(Tensor)的介绍在PyTorch中,Tensor具有许多属性和方法。以下是其中一些关键的属性和方法:属性:H:在标准的PyTorchAPI中并没有直接表示为.H的属性,但在数学或某些库(如NumPy)中,.H通常代表共轭转置(ConjugateTranspose),也称为Hermitiancon
- 基于Dirichlet分布的联邦学习数据分配
黑马算法创新
人工智能机器学习联邦学习异构联邦学习异构数据隐私保护
基于Dirichlet分布的联邦学习数据分配。其目标是将数据按照不均衡的方式分配到不同的客户端,模拟真实世界中客户端数据不均匀的情况。下面详细解释这段逻辑:标签排序和数据组织:首先,代码对数据集中的标签进行排序(labels_sorted)。这些标签代表着数据的类别。然后,通过将标签和相应的数据索引(即数据点的位置)配对,形成了一个名为class_by_labels的列表,每个元素是一个元组,其中
- 三维粗糙表面仿真MATLAB代码
2401_82386822
粗糙表面处理图像处理信号处理matlab数学建模人工智能
表面形貌和粗糙表面仿真MATLAB1.2D数字滤波算法生成高斯和非高斯粗糙表面2.SRM相位频谱表示法生成高斯和非高斯粗糙表面3.NCGM共轭梯度法生成高斯和非高斯粗糙表面4.W-M函数法生成高斯和非高斯粗糙表面5.生成给定均方根偏差Sq,偏度Ssk和峰度Sku非高斯粗糙表面,采用Johnson转换系统以上任意一个方法。6.生成偏度为0,峰度为3的高斯粗糙表面,以上任意一个方法。7.双高斯分层表面
- 表面形貌和粗糙表面仿真MATLAB
2401_82386822
粗糙表面处理信号处理matlabmatlab数学建模图像处理
表面形貌和粗糙表面仿真MATLAB1.2D数字滤波算法生成高斯和非高斯粗糙表面2.SRM相位频谱表示法生成高斯和非高斯粗糙表面3.NCGM共轭梯度法生成高斯和非高斯粗糙表面4.W-M函数法生成高斯和非高斯粗糙表面5.生成给定均方根偏差Sq,偏度Ssk和峰度Sku非高斯粗糙表面,采用Johnson转换系统以上任意一个方法。6.生成偏度为0,峰度为3的高斯粗糙表面,以上任意一个方法。7.双高斯分层表面
- Total Variation Blind Deconvolution论文阅读
青铜锁00
#退化论文阅读论文阅读图像处理
TotalVariationBlindDeconvolution1.论文的研究目标与实际问题意义1.1研究目标1.2实际问题与产业意义2.论文的创新方法、模型与优势2.1核心思路2.2关键公式与技术细节2.2.1联合优化模型2.2.2交替最小化(AM)算法2.2.3预处理与优化加速2.2.4Fixed-Point(FP)算法与预条件共轭梯度(PCG)2.3优势对比3.实验设计与结果3.1实验设计3
- C++:实现共轭梯度方法求解形式为 A*x=b 的线性方程组(附完整源码)
源代码大师
C和C++算法完整教程C和C++实战教程c++算法
C++:实现共轭梯度方法求解形式为A*x=b的线性方程组test.hpptest.cpptest.hppinti4_min(inti1,inti2);double*orth_random(intn,int&seed)
- pytorch,numpy根据权重取值 -- np.random.multinomial,np.random.choice和torch.multinomial函数
*Lisen
pytorchNLPnumpytorchpytochnlp
np.random.multinomial(n,pvals,size=None)->取到的次数分布数组该函数表示根据一个概率数组,取若干次,得到一个次数分布数组参数说明:–n:从矩阵中取值次数;–pvals:根据概率取值,这是一个数组,并且所有数据之和为1;–size:输出的维度,默认为1,即1xpvals例子:a=np.random.rand(6)print(a)#array([0.028634
- 通信算法之260: 时频图谱spectrogram(如短时傅里叶变换STFT)第二讲
秋风战士
算法语音识别人工智能
spectrogram(时频谱图)是一种用于分析信号时频特性的可视化工具,结合了时间与频率维度的能量分布信息。其核心原理与实现要点如下:一、基本定义与原理核心概念Spectrogram通过短时傅里叶变换(STFT)将信号分解为时频二维能量分布,横轴为时间,纵轴为频率,颜色深浅表示能量强度13。实信号频谱具有共轭对称性,通常仅显示正频率部分(单边谱)78。生成流程预加重:提升高频分量
- 线性代数导引:线性算子与共轭线性函数
AI天才研究院
AI大模型企业级应用开发实战AI大模型应用入门实战与进阶DeepSeekR1&大数据AI人工智能大模型计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
线性代数导引:线性算子与共轭线性函数1.背景介绍线性代数是现代数学和计算机科学的基石之一。它不仅在理论研究中占据重要地位,还在实际应用中发挥着关键作用。线性算子和共轭线性函数是线性代数中的两个重要概念,它们在数据分析、机器学习、图像处理等领域有着广泛的应用。本文将深入探讨这两个概念,帮助读者理解其原理、算法和实际应用。2.核心概念与联系2.1线性算子线性算子是从一个向量空间映射到另一个向量空间的函
- 混合精度策略在PBiCGStab算法中的应用
东北豆子哥
HPC/MPICFD/OpenFOAM算法线性代数
混合精度策略在PBiCGStab算法中的应用PBiCGStab(预处理双共轭梯度稳定法)是一种常用的Krylov子空间迭代方法,结合混合精度策略可以显著提高计算效率同时保持足够的精度。下面我将介绍如何在PBiCGStab中实现混合精度,并提供示例代码。混合精度策略概述混合精度策略的核心思想是:使用较低精度(如单精度)进行大部分计算,提高内存带宽利用率和计算速度在关键计算步骤使用较高精度(如双精度)
- LabVIEW基于双通道FFT共轭相乘的噪声抑制
LabVIEW开发
LabVIEW知识LabVIEW参考程序LabVIEW功能LabVIEW伺服阀
对于双通道采集的含噪信号,通过FFT获取复数频谱后,对第二通道频谱取共轭并与第一通道频谱相乘,理论上可增强相关信号成分并抑制非相关噪声。此方法适用于通道间信号高度相关、噪声独立的场景(如共模干扰抑制)。以下为LabVIEW实现方案及案例验证。实现原理与步骤1.核心数学推导设两通道信号为:通道1:S1(t)=Signal(t)+Noise1(t)通道2:S2(t)=Signal(t)+Noise2(
- Eigen3的库使用
憨憨2号
Eigen3c++
文章目录eigen3lib的使用向量向量一元操作向量二元操作共轭矩阵矩阵赋值转置矩阵块操作取行取列取任意大小的块矩阵分解Cholesky分解坐标变换坐标轴旋转旋转矩阵旋转四元数欧拉角旋转向量数据类型转化double数字转化为矩阵eigen3lib的使用向量Eigen::Vector3fu;//3行*1列列向量向量一元操作u.norm();//向量的模u.transpose()//向量的转置向量二元
- 音频进阶学习九——离散时间傅里叶变换DTFT
山河君
#语音信号处理学习信号处理
文章目录前言一、DTFT的解释1.DTFT公式2.DTFT右边释义1)复指数e−jωne^{-j\omegan}e−jωn2)序列与复指数相乘x[n]∗e−jωnx[n]*e^{-j\omegan}x[n]∗e−jωn复指数序列复数的共轭正交正交集3)复指数序列求和3.DTFT左边边释义1)实部与虚部2)幅度与相位二、IDTFT1.逆离散时间的傅里叶变换2.IDTFT验证总结前言按照傅里叶发展的历
- 复变函数与积分变换中的英汉单词对照
River Chandler
物理学与工程学专业英语中英文对照复变函数
复数与复变函数复数complexnumber实部realnumber虚部imaginaryunit纯虚数pureimaginarynumber共轭复数complexconjugatenumber运算operation减法subtraction乘法multiplication除法division复平面complexplane分配律distributerule交换律exchangerule复合函数co
- 【Eigen教程】矩阵操作(三)
十年一梦实验室
矩阵算法线性代数
3.1矩阵运算向下取整向上取整四舍五入正弦余弦正切反正弦反余弦反正切双曲正弦双曲余弦双曲正切有限值检查无穷大检查NaN检查最小值最大值自然对数常用对数指数平方根平方立方幂运算乘法绝对值转置共轭矩阵乘法点积叉积标量乘法标量除法加法减法3.1.1矩阵的加减运算3.1.2标量乘除法3.1.3乘法、点积和叉积3.1.4转置和共轭3.1.5系数运算3.1.6幂和根3.1.7对数和指数3.1.8两个矩阵的最小
- 基于R语言的现代贝叶斯统计学方法(贝叶斯参数估计、贝叶斯回归、贝叶斯计算实践过程
xiao5kou4chang6kai4
统计生态农业r语言回归贝叶斯统计学线性回归
专题一贝叶斯统计学的思想与概念1.1信念函数与概率1.2事件划分与贝叶斯法则1.3稀少事件的概率估计1.4可交换性1.5预测模型的构建专题二单参数模型2.1二项式模型与置信域2.2泊松模型与后验分布2.3指数族模型与共轭先验专题三蒙特卡罗逼近3.1蒙特卡罗方法3.2任意函数的后验推断3.3预测分布采样3.4后验模型检验专题四正态模型4.1均值与条件方差的推断4.2基于数学期望的先验4.3非正态分布
- 潜在狄利克雷分配(Latent Dirichlet Allocation,LDA)—无监督学习方法、概率模型、生成模型、线性模型、非参数化模型、贝叶斯学习、批量学习
剑海风云
ArtificialIntelligence人工智能机器学习潜在狄利克雷分配LDA
定义输入:单词集合W={ω1,⋯ ,ωv,⋯ ,ωV},其中ωv是第v个单词,v=1,2,⋯ ,V,V是单词第个数。单词集合W=\{\omega_1,\cdots,\omega_v,\cdots,\omega_V\},其中\omega_v是第v个单词,v=1,2,\cdots,V,V是单词第个数。单词集合W={ω1,⋯,ωv,⋯,ωV},其中ωv是第v个单词,v=1,2,⋯,V,V是单词第个数。文
- Alkyne-choline,685082-61-5
星贝爱科
Alkyne-choline685082-61-5
物理化学性质Alkyne-choline为棕色油状物质,需要密封避光,储存于阴凉、干燥、通风良好的库房中。它溶于大部分有机溶剂,也溶于水。结构式:概况Alkyne-choline是一种含有炔基基团的试剂,主要用于ClickChemistry。这种试剂可以通过铜催化的点击化学与多种叠氮化合物共轭。Alkyne-choline的分子式为C7H14NO+,分子量为128.19。注意事项在使用Alkyne
- 【机器学习】朴素贝叶斯方法的概率图表示以及贝叶斯统计中的共轭先验方法
Lossya
机器学习概率论人工智能朴素贝叶斯共轭先验
引言朴素贝叶斯方法是一种基于贝叶斯定理的简单概率模型,它假设特征之间相互独立。文章目录引言一、朴素贝叶斯方法的概率图表示1.1节点表示1.2边表示1.3无其他连接1.4总结二、朴素贝叶斯的应用场景2.1文本分类2.2推荐系统2.3医疗诊断2.4欺诈检测2.5情感分析2.6邮件过滤2.7信息检索2.8生物信息学三、朴素贝叶斯的优点四、朴素贝叶斯的局限性4.1特征独立性假设4.2敏感于输入数据的表示4
- 一些可能很有用的矩阵知识
黑洞是不黑
transformer数学理论矩阵线性代数人工智能
一些可有可无的矩阵知识酉矩阵酉矩阵一个服从正态分布的向量乘以一个酉矩阵,得到的向量仍然服从正态分布酉矩阵是一个复数矩阵,满足其转置的共轭等于其逆矩阵。当一个向量通过一个酉矩阵进行线性变换时,它的模长保持不变,只是发生了旋转和缩放。这意味着如果原始向量服从正态分布,变换后的向量仍将服从相同的正态分布。proof:proof:proof:当一个向量服从正态分布时,其概率密度函数(PDF)可以表示为:f
- 共轭矩阵
姜希成
数学概念
共轭矩阵埃尔米特矩阵又称自共轭矩阵、Hermite阵。Hermite阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等(然而矩阵A的共轭矩阵并非Hermite阵)。自共轭矩阵是矩阵本身先转置再把矩阵中每个元素取共轭得到的矩阵。当A=(aij)为复矩阵时,用a¯¯¯a¯表示a的共轭复数,记A¯¯¯¯=(aji¯¯¯¯¯¯)A¯=(aji¯),则A¯¯¯¯A¯为A的共轭矩阵。埃尔米特矩阵(或
- 数学基础 -- 线性代数之酉矩阵
sz66cm
量子计算线性代数
酉矩阵(UnitaryMatrix)酉矩阵是线性代数中一种重要的矩阵类型,特别在量子力学和信号处理等领域有广泛的应用。以下是酉矩阵的定义、性质以及使用和计算的例子。1.定义酉矩阵是一个复矩阵UUU,满足以下条件:U†U=UU†=IU^{\dagger}U=UU^{\dagger}=IU†U=UU†=I其中:U†U^{\dagger}U†是矩阵UUU的共轭转置矩阵,即UUU的转置矩阵再取元素的共轭。
- 利用Python处理合成孔径雷达(SAR)数据的成像过程
wavemenu
python开发语言
本文介绍了利用Python处理合成孔径雷达(SAR)数据的完整成像流程,包括数据加载、基本定义、聚焦、多视处理和结果显示等步骤。测试数据位ERS数据。首先,通过加载包含SAR原始数据的.mat文件,获取数据矩阵并设置相关的传感器参数。接着,定义了两个主要脉冲,即距离向脉冲和方位向脉冲,并对其进行傅里叶变换和共轭运算,得到用于后续相关处理的脉冲模板。在数据聚焦步骤中,通过距离向和方位向的压缩操作,将
- 石墨烯薄膜行业调研报告(一)
方象知产研究院
01石墨烯类别(一)按厚度1.单碳层石墨烯(singlelayergraphene):由单个碳原子层构成的大平面共轭结构材料,目前石墨烯的大多数奇特性质都是基于此材料2.多层石墨烯或少数碳层石墨烯(afewlayergraphene):厚度在2~10碳层的石墨薄片材料,研究表明,其层内电子运动行为有别于石墨烯材料3.石墨烯微片(graphenenonaplatelets):厚度在10~100纳米厚
- 反式脂肪酸,你猜它是什么酸?
DaobiDoumi
反式脂肪酸?反式脂肪酸是不饱和脂肪酸的一种,其化学结构上多了“非共轭反式双键”。反式脂肪酸的主要来源①是天然食物、反刍动物,如牛、羊、猪等的肉、脂肪、乳及乳制品;②是通过加工产生,主要是植物油的氢化和精炼,另外,食物的煎炒烹炸也会产生少量的反式脂肪酸。TIPS:植物油氢化后可以提升口感,同时延长保质期。反式脂肪酸吃多了会怎么样?○形成血栓。反式脂肪酸会增加人体血液的粘稠度和凝聚力,容易导致血栓的形
- 量子算法入门——3.狄拉克符号与量子态(3)
鸥梨菌Honevid
Quantum算法
3.狄拉克符号的数学基础左矢是右矢的共轭+转置上标*表示共轭算符就是对狄拉克符号进行操作,就是相当于矩阵操作向量,算符对应本征值和本征态本征值:拉伸x、y向量的程度本征态:x、y向量上标匕首符号(或称十字符号,dagger符号),意义就是转置+共轭实数的共轭就是它自己必须在选择基底之后,算符才能记为矩阵,否则还是一个量子态
- 人、机、环境及态、势、感、知之间的共轭
人机与认知实验室
机器学习决策树算法人工智能数据挖掘
一、共轭的本质在数学中,共轭通常指两个复数中的一个与另一个具有相同的实部但虚部互为相反数。例如,对于复数a+bi,其共轭是a-bi。共轭的本质在于保持复数的实部不变,但改变虚部的符号,从而使两个复数在某种程度上具有对称性。在线性代数中,共轭也可以指两个向量之间的关系。对于复数向量,共轭就是将向量的每个元素取共轭。在这种意义上,共轭的本质是在保持向量的长度和方向不变的同时改变其元素的符号。在语言学中
- 盘点大学里那些好用的7款搜题软件! #经验分享#微信
笑笑18178
经验分享
收录大学专业的多种习题,不管是网课答案还是教材习题,都能在这里找到答案,而且还有四六级、考公、考研等备考资料,很是实用。它的搜题模式也是比较丰富的,支持文字搜题、拍照搜题、扫码搜书等搜题模式,轻松解决学习上的难题。1.七燕搜题这是一个公众号同时支持大学生和上班族的一款在线网站,包括财经,注册会计师,计算机,招录类,学历类,医学类等等。下方附上一些测试的试题及答案1、物象空间折射率相同时,共轭光学系
- 矩阵的正定(positive definite)性质的作用
blogZT
数学矩阵线性代数
1.定义注意,本文中正定和半正定矩阵不要求是对称或Hermite的。2.性质3.作用(1)Ax=b直接法求解cholesky实对称正定矩阵求解复共轭对称正定矩阵求解LDL实对称非正定矩阵求解复共轭对称非正定矩阵求解复对称矩阵求解LU实非对称矩阵求解复非对称矩阵求解(2)特征值求解在ARPACK(隐式重启Arnoldi算法)中,对K*x=lambda*M*x该广义特征值问题M必须得是ModeOper
- e^{ix} 的 conjugate value(复共轭)
勤奋的大熊猫
数学数学
e^{ix}的conjugatevalue正文实数的复共轭eixe^{ix}eix的复共轭推导正文这里简单说明一下eixe^{ix}eix的复共轭。实数的复共轭首先,我们知道,所谓复共轭是针对复数而言的。对于实数,我们知道,实数集被复数集包含。因此,实数也可以看作是一个复数,比如,对于实数xxx,其复数形式为:x+i⋅0(1)x+i\cdot0\tag{1}x+i⋅0(1)复共轭的操作是对复数的虚
- 关于旗正规则引擎中的MD5加密问题
何必如此
jspMD5规则加密
一般情况下,为了防止个人隐私的泄露,我们都会对用户登录密码进行加密,使数据库相应字段保存的是加密后的字符串,而非原始密码。
在旗正规则引擎中,通过外部调用,可以实现MD5的加密,具体步骤如下:
1.在对象库中选择外部调用,选择“com.flagleader.util.MD5”,在子选项中选择“com.flagleader.util.MD5.getMD5ofStr({arg1})”;
2.在规
- 【Spark101】Scala Promise/Future在Spark中的应用
bit1129
Promise
Promise和Future是Scala用于异步调用并实现结果汇集的并发原语,Scala的Future同JUC里面的Future接口含义相同,Promise理解起来就有些绕。等有时间了再仔细的研究下Promise和Future的语义以及应用场景,具体参见Scala在线文档:http://docs.scala-lang.org/sips/completed/futures-promises.html
- spark sql 访问hive数据的配置详解
daizj
spark sqlhivethriftserver
spark sql 能够通过thriftserver 访问hive数据,默认spark编译的版本是不支持访问hive,因为hive依赖比较多,因此打的包中不包含hive和thriftserver,因此需要自己下载源码进行编译,将hive,thriftserver打包进去才能够访问,详细配置步骤如下:
1、下载源码
2、下载Maven,并配置
此配置简单,就略过
- HTTP 协议通信
周凡杨
javahttpclienthttp通信
一:简介
HTTPCLIENT,通过JAVA基于HTTP协议进行点与点间的通信!
二: 代码举例
测试类:
import java
- java unix时间戳转换
g21121
java
把java时间戳转换成unix时间戳:
Timestamp appointTime=Timestamp.valueOf(new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date()))
SimpleDateFormat df = new SimpleDateFormat("yyyy-MM-dd hh:m
- web报表工具FineReport常用函数的用法总结(报表函数)
老A不折腾
web报表finereport总结
说明:本次总结中,凡是以tableName或viewName作为参数因子的。函数在调用的时候均按照先从私有数据源中查找,然后再从公有数据源中查找的顺序。
CLASS
CLASS(object):返回object对象的所属的类。
CNMONEY
CNMONEY(number,unit)返回人民币大写。
number:需要转换的数值型的数。
unit:单位,
- java jni调用c++ 代码 报错
墙头上一根草
javaC++jni
#
# A fatal error has been detected by the Java Runtime Environment:
#
# EXCEPTION_ACCESS_VIOLATION (0xc0000005) at pc=0x00000000777c3290, pid=5632, tid=6656
#
# JRE version: Java(TM) SE Ru
- Spring中事件处理de小技巧
aijuans
springSpring 教程Spring 实例Spring 入门Spring3
Spring 中提供一些Aware相关de接口,BeanFactoryAware、 ApplicationContextAware、ResourceLoaderAware、ServletContextAware等等,其中最常用到de匙ApplicationContextAware.实现ApplicationContextAwaredeBean,在Bean被初始后,将会被注入 Applicati
- linux shell ls脚本样例
annan211
linuxlinux ls源码linux 源码
#! /bin/sh -
#查找输入文件的路径
#在查找路径下寻找一个或多个原始文件或文件模式
# 查找路径由特定的环境变量所定义
#标准输出所产生的结果 通常是查找路径下找到的每个文件的第一个实体的完整路径
# 或是filename :not found 的标准错误输出。
#如果文件没有找到 则退出码为0
#否则 即为找不到的文件个数
#语法 pathfind [--
- List,Set,Map遍历方式 (收集的资源,值得看一下)
百合不是茶
listsetMap遍历方式
List特点:元素有放入顺序,元素可重复
Map特点:元素按键值对存储,无放入顺序
Set特点:元素无放入顺序,元素不可重复(注意:元素虽然无放入顺序,但是元素在set中的位置是有该元素的HashCode决定的,其位置其实是固定的)
List接口有三个实现类:LinkedList,ArrayList,Vector
LinkedList:底层基于链表实现,链表内存是散乱的,每一个元素存储本身
- 解决SimpleDateFormat的线程不安全问题的方法
bijian1013
javathread线程安全
在Java项目中,我们通常会自己写一个DateUtil类,处理日期和字符串的转换,如下所示:
public class DateUtil01 {
private SimpleDateFormat dateformat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
public void format(Date d
- http请求测试实例(采用fastjson解析)
bijian1013
http测试
在实际开发中,我们经常会去做http请求的开发,下面则是如何请求的单元测试小实例,仅供参考。
import java.util.HashMap;
import java.util.Map;
import org.apache.commons.httpclient.HttpClient;
import
- 【RPC框架Hessian三】Hessian 异常处理
bit1129
hessian
RPC异常处理概述
RPC异常处理指是,当客户端调用远端的服务,如果服务执行过程中发生异常,这个异常能否序列到客户端?
如果服务在执行过程中可能发生异常,那么在服务接口的声明中,就该声明该接口可能抛出的异常。
在Hessian中,服务器端发生异常,可以将异常信息从服务器端序列化到客户端,因为Exception本身是实现了Serializable的
- 【日志分析】日志分析工具
bit1129
日志分析
1. 网站日志实时分析工具 GoAccess
http://www.vpsee.com/2014/02/a-real-time-web-log-analyzer-goaccess/
2. 通过日志监控并收集 Java 应用程序性能数据(Perf4J)
http://www.ibm.com/developerworks/cn/java/j-lo-logforperf/
3.log.io
和
- nginx优化加强战斗力及遇到的坑解决
ronin47
nginx 优化
先说遇到个坑,第一个是负载问题,这个问题与架构有关,由于我设计架构多了两层,结果导致会话负载只转向一个。解决这样的问题思路有两个:一是改变负载策略,二是更改架构设计。
由于采用动静分离部署,而nginx又设计了静态,结果客户端去读nginx静态,访问量上来,页面加载很慢。解决:二者留其一。最好是保留apache服务器。
来以下优化:
- java-50-输入两棵二叉树A和B,判断树B是不是A的子结构
bylijinnan
java
思路来自:
http://zhedahht.blog.163.com/blog/static/25411174201011445550396/
import ljn.help.*;
public class HasSubtree {
/**Q50.
* 输入两棵二叉树A和B,判断树B是不是A的子结构。
例如,下图中的两棵树A和B,由于A中有一部分子树的结构和B是一
- mongoDB 备份与恢复
开窍的石头
mongDB备份与恢复
Mongodb导出与导入
1: 导入/导出可以操作的是本地的mongodb服务器,也可以是远程的.
所以,都有如下通用选项:
-h host 主机
--port port 端口
-u username 用户名
-p passwd 密码
2: mongoexport 导出json格式的文件
- [网络与通讯]椭圆轨道计算的一些问题
comsci
网络
如果按照中国古代农历的历法,现在应该是某个季节的开始,但是由于农历历法是3000年前的天文观测数据,如果按照现在的天文学记录来进行修正的话,这个季节已经过去一段时间了。。。。。
也就是说,还要再等3000年。才有机会了,太阳系的行星的椭圆轨道受到外来天体的干扰,轨道次序发生了变
- 软件专利如何申请
cuiyadll
软件专利申请
软件技术可以申请软件著作权以保护软件源代码,也可以申请发明专利以保护软件流程中的步骤执行方式。专利保护的是软件解决问题的思想,而软件著作权保护的是软件代码(即软件思想的表达形式)。例如,离线传送文件,那发明专利保护是如何实现离线传送文件。基于相同的软件思想,但实现离线传送的程序代码有千千万万种,每种代码都可以享有各自的软件著作权。申请一个软件发明专利的代理费大概需要5000-8000申请发明专利可
- Android学习笔记
darrenzhu
android
1.启动一个AVD
2.命令行运行adb shell可连接到AVD,这也就是命令行客户端
3.如何启动一个程序
am start -n package name/.activityName
am start -n com.example.helloworld/.MainActivity
启动Android设置工具的命令如下所示:
# am start -
- apache虚拟机配置,本地多域名访问本地网站
dcj3sjt126com
apache
现在假定你有两个目录,一个存在于 /htdocs/a,另一个存在于 /htdocs/b 。
现在你想要在本地测试的时候访问 www.freeman.com 对应的目录是 /xampp/htdocs/freeman ,访问 www.duchengjiu.com 对应的目录是 /htdocs/duchengjiu。
1、首先修改C盘WINDOWS\system32\drivers\etc目录下的
- yii2 restful web服务[速率限制]
dcj3sjt126com
PHPyii2
速率限制
为防止滥用,你应该考虑增加速率限制到您的API。 例如,您可以限制每个用户的API的使用是在10分钟内最多100次的API调用。 如果一个用户同一个时间段内太多的请求被接收, 将返回响应状态代码 429 (这意味着过多的请求)。
要启用速率限制, [[yii\web\User::identityClass|user identity class]] 应该实现 [[yii\filter
- Hadoop2.5.2安装——单机模式
eksliang
hadoophadoop单机部署
转载请出自出处:http://eksliang.iteye.com/blog/2185414 一、概述
Hadoop有三种模式 单机模式、伪分布模式和完全分布模式,这里先简单介绍单机模式 ,默认情况下,Hadoop被配置成一个非分布式模式,独立运行JAVA进程,适合开始做调试工作。
二、下载地址
Hadoop 网址http:
- LoadMoreListView+SwipeRefreshLayout(分页下拉)基本结构
gundumw100
android
一切为了快速迭代
import java.util.ArrayList;
import org.json.JSONObject;
import android.animation.ObjectAnimator;
import android.os.Bundle;
import android.support.v4.widget.SwipeRefreshLayo
- 三道简单的前端HTML/CSS题目
ini
htmlWeb前端css题目
使用CSS为多个网页进行相同风格的布局和外观设置时,为了方便对这些网页进行修改,最好使用( )。http://hovertree.com/shortanswer/bjae/7bd72acca3206862.htm
在HTML中加入<table style=”color:red; font-size:10pt”>,此为( )。http://hovertree.com/s
- overrided方法编译错误
kane_xie
override
问题描述:
在实现类中的某一或某几个Override方法发生编译错误如下:
Name clash: The method put(String) of type XXXServiceImpl has the same erasure as put(String) of type XXXService but does not override it
当去掉@Over
- Java中使用代理IP获取网址内容(防IP被封,做数据爬虫)
mcj8089
免费代理IP代理IP数据爬虫JAVA设置代理IP爬虫封IP
推荐两个代理IP网站:
1. 全网代理IP:http://proxy.goubanjia.com/
2. 敲代码免费IP:http://ip.qiaodm.com/
Java语言有两种方式使用代理IP访问网址并获取内容,
方式一,设置System系统属性
// 设置代理IP
System.getProper
- Nodejs Express 报错之 listen EADDRINUSE
qiaolevip
每天进步一点点学习永无止境nodejs纵观千象
当你启动 nodejs服务报错:
>node app
Express server listening on port 80
events.js:85
throw er; // Unhandled 'error' event
^
Error: listen EADDRINUSE
at exports._errnoException (
- C++中三种new的用法
_荆棘鸟_
C++new
转载自:http://news.ccidnet.com/art/32855/20100713/2114025_1.html
作者: mt
其一是new operator,也叫new表达式;其二是operator new,也叫new操作符。这两个英文名称起的也太绝了,很容易搞混,那就记中文名称吧。new表达式比较常见,也最常用,例如:
string* ps = new string("
- Ruby深入研究笔记1
wudixiaotie
Ruby
module是可以定义private方法的
module MTest
def aaa
puts "aaa"
private_method
end
private
def private_method
puts "this is private_method"
end
end