车载多传感器融合定位方案Pipeline：IMU，CNSS，LIDAR

为什么用IMU, CNSS, LIDAR的组合

IMU可以提供连续的位置信息，以补充GNSS可能因为地形等原因缺失的数据信息
GNSS可以提供绝对的位置信息，减轻IMU累积的数据漂移问题
LIDAR可以根据准确的周边信息，确定自己在地图中的位置
三者可相互补充共同确定车辆的状态和所处位置

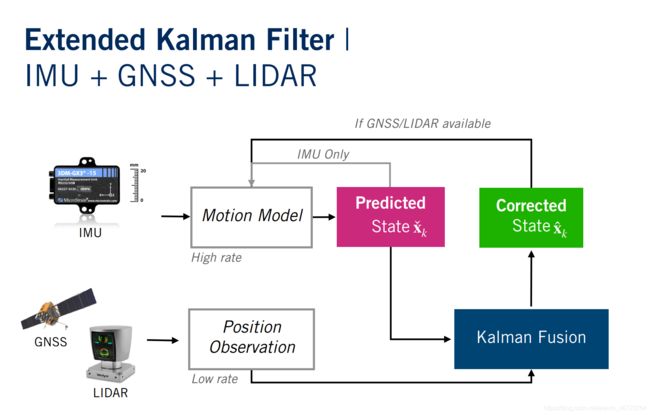
整体流程图

整个方案的大体思路为：将IMU数据作为输入带入运动学方程计算nominal state，当其他观测数据available时，将其带入计算车辆error state,然后两者相加得出最终的更正状态，用于后续迭代。当没有观测数据时，就将预测数据作为结果进行迭代。

采用这种方式的好处是：将最终的true state的确定分成了两个，nominal state只和状态方程和输入有关，这样一来我们就能很方便的在方程上增加想要的约束。
另一个好处在于能很好地处理传感器数据暂时丢失的问题。有观测数据的时候就拿来修正状态，没有的时候就用预测状态，应用起来比较flexible。当然只用IMU时，数据漂移现象还是没法避免，个人感觉在这种情况下，可能还需要camera辅助。

1. 同步传感器坐标系

通常情况下，IMU和GNSS数据用的是车身坐标系，而LIDAR坐标系与传感器on board位置相关，因此要将LIDAR数据转换到车身坐标系，完成传感器数据坐标系的统一

C_li = np.array([
     [ 0.9975 , -0.04742,  0.05235],
     [ 0.04992,  0.99763, -0.04742],
     [-0.04998,  0.04992,  0.9975 ]
])

t_i_li = np.array([0.5, 0.1, 0.5])

# Transform from the LIDAR frame to the vehicle (IMU) frame.
lidar.data = (C_li @ lidar.data.T).T + t_i_li

2. 设置预估传感器方差和噪音常量

这是滤波器最重要的方面之一，如果出现标定错误或者数据丢失时，通常需要调整传感器方差进行补偿。

var_imu_f = 0.10
var_imu_w = 0.001
var_gnss  = 0.01
var_lidar = 100

g = np.array([0, 0, -9.81])  # gravity 1x3
l_jac = np.zeros([9, 6])
l_jac[3:, :] = np.eye(6)  # motion model noise jacobian
h_jac = np.zeros([3, 9])
h_jac[:, :3] = np.eye(3)  # measurement model jacobian

3. 设置ES-EKF初始变量值

车辆状态包括：位置P_k(3,1), 速度V_k(3,1)，姿态q_k(4,1)
IMU数据作为Motion model 的输入：比力f_k(3,1), 角速度(3,1)
同时分别设置Gnss/LIDAR数据索引，因为这些数据并不能100%随时获得，和带有各自的时间戳

p_est = np.zeros([imu_f.data.shape[0], 3])  # position estimates
v_est = np.zeros([imu_f.data.shape[0], 3])  # velocity estimates
q_est = np.zeros([imu_f.data.shape[0], 4])  # orientation estimates as quaternions
p_cov = np.zeros([imu_f.data.shape[0], 9, 9])  # covariance matrices at each timestep

# Set initial values.
p_est[0] = gt.p[0]  #p_est.shape (10918, 3)
v_est[0] = gt.v[0]
q_est[0] = Quaternion(euler=gt.r[0]).to_numpy()
p_cov[0] = np.zeros(9)  # covariance of estimate
gnss_i  = 0  #index of gnss/lidar data
lidar_i = 0

4. 根据IMU数据预估车辆状态-prediction

IMU数据作为输入，根据motion model 预测车辆状态

    # 1. Update state with IMU inputs
    #orientation of THE sensor why*? Cns
    rotation_matrix = Quaternion(*q_est[k - 1]).to_mat()  #.shape = 3x3

    # 1.1 Linearize the motion model and compute Jacobians  3x1; 3x1, 4x1
    p_est[k] = p_est[k-1] + delta_t*v_est[k-1] + (delta_t**2/2)*(rotation_matrix.dot(imu_f.data[k-1])+g)
    v_est[k] = v_est[k-1] + delta_t*(rotation_matrix.dot(imu_f.data[k-1])+g)
    q_est[k] = Quaternion(axis_angle=imu_w.data[k-1]*delta_t).quat_mult_right(q_est[k-1])
    #predicted data used when external data is not available
    

同时需要计算雅可比矩阵
雅可比矩阵的含义及表达：

计算结果

    F = np.identity(9)
    #given in C2M5L2
    F[:3,3:6] = delta_t*np.identity(3)
    F[3:6,6:] = -(rotation_matrix.dot(skew_symmetric(imu_f.data[k-1].reshape((3,1)))))

    #measurement noise given in C2M5L2
    Q = np.identity(6)
    Q[:,:3] *= (delta_t**2)*var_imu_f
    Q[:,-3:] *= (delta_t**2)*var_imu_w
    # 2. Propagate uncertainty
    p_cov[k] = F.dot(p_cov[k-1]).dot(F.T) + l_jac.dot(Q).dot(l_jac.T)

在其他传感器数据non available的情况下，在这里计算出来的predicted state就是下一轮更新用的true state

5. 检测GNSS或LIDAR数据可用性

当与IMU数据时间戳对应的LIDAR/GNSS数据存在时，对车辆状态进行更新。

    # 3. Check availability of GNSS and LIDAR measurements : only part value get corrected
    #don't forget to check for time consistance
    if lidar_i<lidar.t.shape[0] and lidar.t[lidar_i] == imu_f.t[k-1]:
        #y_k need to be a 3x1 vector, lidar.data[lidar_i].shape (,3)
        y_k = lidar.data[lidar_i].T
        p_est[k], v_est[k], q_est[k], p_cov[k] = measurement_update(var_lidar,p_cov[k],y_k,p_est[k],v_est[k],q_est[k])
        lidar_i += 1

    if gnss_i<gnss.t.shape[0] and gnss.t[gnss_i] == imu_f.t[k-1]:
        y_k = gnss.data[gnss_i].T
        p_est[k], v_est[k], q_est[k], p_cov[k] = measurement_update(var_gnss, p_cov[k], y_k, p_est[k], v_est[k], q_est[k])
        gnss_i += 1

6. 利用GNSS/LIDAR的测量数据对车辆状态更正-correction

计算卡尔曼增益和error state,然后更正预测状态(predicted state)，最后更新协方差

    # 3.1 Compute Kalman Gain
    #R need to be 3x3 : h_jac.dot(p_cov_check).dot(h_jac.T) 3x9 9x9 9x3 shape = 3x3
    I = np.identity(3)
    R = I*sensor_var

    #K.shape = 9x9 9x3 3x3 = 9x3
    K = p_cov_check.dot(h_jac.T).dot(np.linalg.inv(h_jac.dot(p_cov_check).dot(h_jac.T)+R))

    # 3.2 Compute error state
    #error.shape = 9x3 (3x1-3x1) = 9x1
    error = K.dot(y_k - p_check) #shape(9,)

    p_del = error[:3]
    v_del = error[3:6]
    phi_del = error[6:]

    # 3.3 Correct predicted state
    p_hat = p_check + p_del
    v_hat = v_check + v_del
    q_hat = Quaternion(euler=phi_del).quat_mult_right(q_check) #4x1

    # 3.4 Compute corrected covariance
    p_cov_hat = (np.identity(9) - K.dot(h_jac)).dot(p_cov_check)

    #Output: p_hat 3x1; v_hat 3x1; q_hat 4x1; p_cov_hat 9x9
    return p_hat, v_hat, q_hat, p_cov_hat

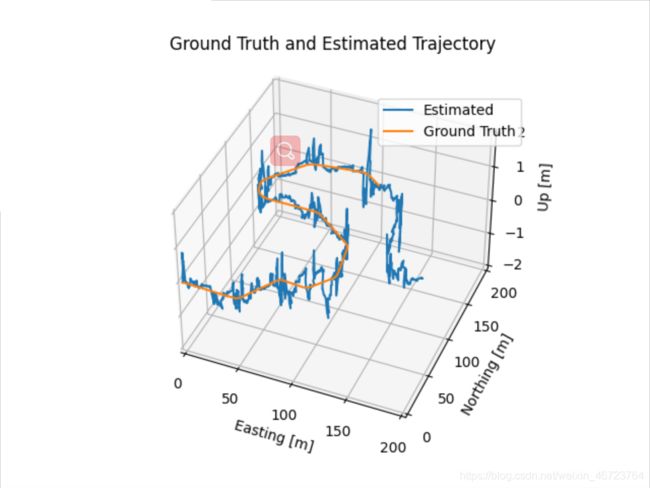
7. 结果

从效果来看位置误差在5之间，姿态误差0.5左右，较好的预测了车辆状态。