本科课程【数据结构与算法】实验6 - 创建哈希表、最短路径（Dijkstra算法）

大家好，我是【1+1=王】， 热爱java的计算机（人工智能）渣硕研究生在读。
如果你也对java、人工智能等技术感兴趣，欢迎关注，抱团交流进大厂！！！
Good better best, never let it rest, until good is better, and better best.

近期会把自己本科阶段的一些课程设计、实验报告等分享出来，供大家参考，希望对大家有帮助。

博客更新至专栏【课程设计实验报告】：https://blog.csdn.net/weixin_43598687/category_11640051.html

一、 实验目的

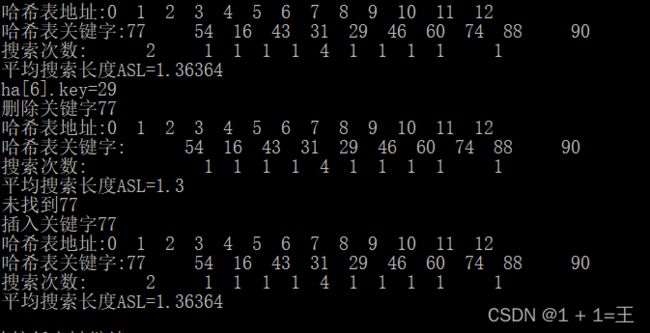
1. 实现哈希表的创建
2. 利用线性探测在散列处理冲突
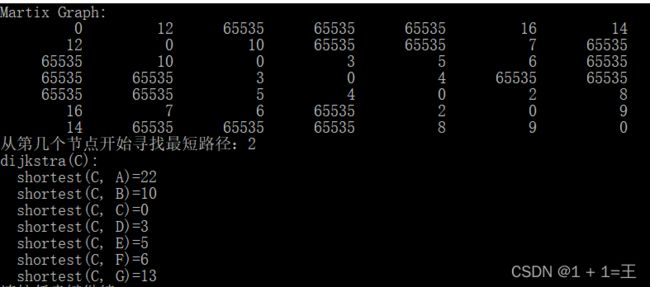
3. 掌握图的邻接矩阵表示
4. 实现图的最短路径查找操作（Di jkstra算法）

二、 实验内容

1. 实验任务

（1）创建哈希表
（2）利用Di jkstra算法寻找图的最短路径

2. 程序设计

1） 数据输入（输入哪些数据、个数、类型、来源、输入方式）
输入哈希表的关键数key（int 整型）

图的顶点数据（data）char字符型；
图的边关系（v1,v2）int 整型；
各边的权值（w）int 整型

2） 数据存储（输入数据在内存中的存储）
定义结构体Hash（key，si）
以数组HashList[i]存储各条数据

采用邻接矩阵存储图

3） 数据处理（说明处理步骤。若不是非常简单，需要绘制流程图）
（1）
①哈希表的查找
储存数据时，将数据存入通过哈希函数所得的地址里，使用同一个哈希函数通过关键字key计算出储存地址，通过该地址访问到查找的记录
②冲突解决
使用线性探测再散列法（冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表）
（2）
在所有从源点出发的弧中选取一条权值最小的弧，即为第一条最短路径；
设置一个顶点集合S，存放最短路径的终点。顶点k为当前最短路径的终点，将Vk加入集合S中，而Dist[k]为最短路径的长度；
每次从集合V-S中取出具有最短特殊路径长度的顶点u，将u加到S中，同时对数组Dist做必要的修改，若Dist[u]+G.arcs[u][k] 重复操作2）、3）共n-1次1

4） 数据输出

三、 实验环境

1. 操作系统：WINDOWS 10
2. 开发工具：VC++ 2013
3. 实验设备：PC

源代码（C++实现）

创建哈希表

#include 
#include
using namespace std;

#define MaxSize 100      //定义最大哈希表长度
#define NULLKEY -1       //定义空关键字值
#define DELKEY -2        //定义被删关键字值
typedef int KeyType;     //关键字类型
typedef char *InfoType;  //其他数据类型

typedef struct{
	KeyType key;        //关键字域
	InfoType data;      //其他数据域
	int count;          //探查次数域
}HashTable[MaxSize];    //哈希表类型

void InsertHT(HashTable ha, int &n, KeyType k, int p);
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p);
int SearchHT(HashTable ha, int p, KeyType k);
int DeleteHT(HashTable ha, int p, int k, int &n);
void DispHT(HashTable ha, int n, int m);
void CompASL(HashTable ha, int m);

void main()
{
	int x[] = { 16, 74, 60, 43, 54, 90, 46, 31, 29, 88, 77 };
	int n = 11, m = 13, p = 13, i, k = 29;
	HashTable ha;
	CreateHT(ha, x, n, m, p);
	cout << endl;
	DispHT(ha, n, m);
	i = SearchHT(ha, p, k);
	if (i != -1)
		printf(" ha[%d].key=%d\n", i, k);
	else
		cout << "未找到" << k << endl;
	k = 77;
	printf(" 删除关键字%d\n", k);
	DeleteHT(ha, p, k, n);
	DispHT(ha, n, m);
	i = SearchHT(ha, p, k);
	if (i != -1)
		printf(" ha[%d].key=%d\n", i, k);
	else
		printf(" 未找到%d\n", k);
	printf(" 插入关键字%d\n", k);
	InsertHT(ha, n, k, p);
	DispHT(ha, n, m);
	cout << endl;
	system("pause");
}

//将关键字k插入到哈希表中
void InsertHT(HashTable ha, int &n, KeyType k, int p)
{
	int i, adr;
	adr = k%p;
	if (ha[adr].key == NULLKEY || ha[adr].key == DELKEY)  
	{
		ha[adr].key = k;
		ha[adr].count = 1;
	}
	else      //发生冲突时,采用线性探查法解决冲突
	{
		i = 1;  
		do
		{
			adr = (adr + 1) % p;
			i++;
		} while (ha[adr].key != NULLKEY && ha[adr].key != DELKEY);
		ha[adr].key = k;
		ha[adr].count = i;
	}
	n++;
}

//创建哈希表
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p)
{
	int i, n1 = 0;
	for (i = 0; i<m; i++)  //哈希表置初值
	{
		ha[i].key = NULLKEY;
		ha[i].count = 0;
	}
	for (i = 0; i<n; i++)
		InsertHT(ha, n1, x[i], p);
}

//在哈希表中查找关键字k
int SearchHT(HashTable ha, int p, KeyType k)
{
	int i = 0, adr;
	adr = k%p;
	while (ha[adr].key != NULLKEY && ha[adr].key != k)
	{
		i++;             //采用线性探查法找下一个地址
		adr = (adr + 1) % p;
	}
	if (ha[adr].key == k)  //查找成功
		return adr;
	else                //查找失败
		return -1;

}

//删除哈希表中关键字k
int DeleteHT(HashTable ha, int p, int k, int &n)
{
	int adr;
	adr = SearchHT(ha, p, k);
	if (adr != -1)   //在哈希表中找到关键字
	{
		ha[adr].key = DELKEY;
		n--;       //哈希表长度减1
		return 1;
	}
	else            //在哈希表中未找到该关键字
		return 0;

}

//输出哈希表
void DispHT(HashTable ha, int n, int m)
{
	float avg = 0;
	int i;
	cout<<" 哈希表地址:";
	for (i = 0; i<m; i++)
		cout<<i<<"  ";
	cout << endl;
	cout<<" 哈希表关键字:";
	for (i = 0; i<m; i++)
	if (ha[i].key == NULLKEY || ha[i].key == DELKEY)
		cout<<"   "; 
	else
		cout<<ha[i].key<<"  ";
	cout<<endl;
	cout<<" 搜索次数:\t";
	for (i = 0; i<m; i++)
	if (ha[i].key == NULLKEY || ha[i].key == DELKEY)
		cout<<"   "; 
	else
		cout<<ha[i].count<<"  ";
	cout << endl;
	for (i = 0; i<m; i++)
	if (ha[i].key != NULLKEY && ha[i].key != DELKEY)
		avg = avg + ha[i].count;
	avg = avg / n;
	cout << " 平均搜索长度ASL=" << avg << endl;

}

//查找成功时，平均查找长度
void CompASL(HashTable ha, int m)
{
	int i;
	int s = 0, n = 0;
	for (i = 0; i<m; i++)
	if (ha[i].key != DELKEY && ha[i].key != NULLKEY)
	{
		s = s + ha[i].count;
		n++;
	}
	printf(" 查找成功的ASL=%.3g\n", s*1.0 / n);

}

最短路径

#include 
#include 
#include
#include 
using namespace std;

#define MAX         100                 // 矩阵最大容量
#define INF         65535        		// 最大值65535
#define LENGTH(a)   (sizeof(a)/sizeof(a[0]))

// 图的邻接矩阵存储
typedef struct _graph

{
	char vexs[MAX];       // 顶点集合
	int vexnum;           // 顶点数
	int edgnum;           // 边数
	int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
	char start; // 边的起点
	char end;   // 边的终点
	int weight; // 边的权重
}EData;

Graph* create_graph();
void print_graph(Graph G);
void dijkstra(Graph G, int vs, int prev[], int dist[]);

int main()
{
	int vs;
	int prev[MAX] = { 0 };
	int dist[MAX] = { 0 };
	Graph* pG;
	pG = create_graph();
	print_graph(*pG);       // 打印图
	cout << "从第几个节点开始寻找最短路径：";
	cin >> vs;
	dijkstra(*pG, vs, prev, dist);
	system("pause");
	return 0;
}

/*
* 创建图(用已提供的矩阵)
*/
Graph* create_graph()
{
	char vexs[] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
	int matrix[][9] = {
		/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
		/*A*/{ 0, 12, INF, INF, INF, 16, 14 },
		/*B*/{ 12, 0, 10, INF, INF, 7, INF },
		/*C*/{ INF, 10, 0, 3, 5, 6, INF },
		/*D*/{ INF, INF, 3, 0, 4, INF, INF },
		/*E*/{ INF, INF, 5, 4, 0, 2, 8 },
		/*F*/{ 16, 7, 6, INF, 2, 0, 9 },
		/*G*/{ 14, INF, INF, INF, 8, 9, 0 } };

	int vlen = LENGTH(vexs);
	int i, j;
	Graph* pG;
	pG = (Graph*)malloc(sizeof(Graph));
	pG->vexnum = vlen;
	for (i = 0; i < pG->vexnum; i++)
		pG->vexs[i] = vexs[i];
	for (i = 0; i < pG->vexnum; i++)
	{
		for (j = 0; j < pG->vexnum; j++)
			pG->matrix[i][j] = matrix[i][j];
	}
	for (i = 0; i < pG->vexnum; i++)
	{
		for (j = 0; j < pG->vexnum; j++)
		if (i != j && pG->matrix[i][j] != INF)
			pG->edgnum++;
	}
	pG->edgnum /= 2;
	return pG;
}

/*
* 打印矩阵队列图
*/

void print_graph(Graph G)
{
	int i, j;
	cout << "Martix Graph:" << endl;;
	for (i = 0; i < G.vexnum; i++)
	{
		for (j = 0; j < G.vexnum; j++)
			printf("%10d ", G.matrix[i][j]);
		cout << endl;
	}
}



/*
* Dijkstra最短路径。
* 统计图(G)中"顶点vs"到其它各个顶点的最短路径。
*
* 参数说明：
*        G -- 图
*       vs -- 起始顶点(start vertex)。计算"顶点vs"到其它顶点的最短路径。
*     prev -- 前驱顶点数组。
*     dist -- 长度数组。
*/
void dijkstra(Graph G, int vs, int prev[], int dist[])
{
	int i, j, k;
	int min;
	int tmp;
	int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
	// 初始化
	for (i = 0; i < G.vexnum; i++)
	{
		flag[i] = 0;              // 顶点i的最短路径还没获取到。
		prev[i] = 0;              // 顶点i的前驱顶点为0。
		dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
	}
	// 对"顶点vs"自身进行初始化
	flag[vs] = 1;
	dist[vs] = 0;
	// 遍历G.vexnum-1次；每次找出一个顶点的最短路径。
	for (i = 1; i < G.vexnum; i++)
	{
		// 寻找当前最小的路径；
		min = INF;
		for (j = 0; j < G.vexnum; j++)
		{
			if (flag[j] == 0 && dist[j]<min)
			{
				min = dist[j];
				k = j;
			}
		}
		// 标记"顶点k"为已经获取到最短路径
		flag[k] = 1;
		// 修正当前最短路径和前驱顶点
		// 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
		for (j = 0; j < G.vexnum; j++)
		{
			tmp = (G.matrix[k][j] == INF ? INF : (min + G.matrix[k][j])); // 防止溢出
			if (flag[j] == 0 && (tmp  < dist[j]))
			{
				dist[j] = tmp;
				prev[j] = k;
			}
		}
	}
	// 打印dijkstra最短路径的结果
	printf("dijkstra(%c): \n", G.vexs[vs]);
	for (i = 0; i < G.vexnum; i++)
		printf("  shortest(%c, %c)=%d\n", G.vexs[vs], G.vexs[i], dist[i]);
}

博客更新至专栏【课程设计实验报告】：https://blog.csdn.net/weixin_43598687/category_11640051.html