欠拟合和过拟合——【torch学习笔记】

欠拟合和过拟合

引用翻译：《动手学深度学习》

当我们比较训练和验证误差时，我们要注意两种常见的情况。首先，我们要注意我们的训练误差和验证误差都很大，但两者之间有一点差距的情况。如果模型无法减少训练误差，这可能意味着我们的模型过于简单（即表达能力不足），无法捕捉到我们试图建模的模式。此外，由于我们的训练和验证误差之间的泛化差距很小，我们有理由相信，我们可以用一个更复杂的模型来解决。这种现象被称为欠拟合。

另一方面，正如我们上面所讨论的，我们要注意的是，当我们的训练误差明显低于验证误差时，表明严重的过拟合。请注意，过拟合并不总是一件坏事。特别是在深度学习方面，众所周知，最好的预测模型在训练数据上的表现往往远远好于保持数据。

最终，我们通常更关心验证误差而不是训练和验证误差之间的差距。我们是过拟合还是欠拟合，既取决于我们模型的复杂性，也取决于可用的训练数据集的大小，我们在下面讨论这两个话题。

一、模型复杂度

为了说明一些关于过拟合和模型复杂性的经典直觉，我们给出了一个使用多项式的例子。给出由单一特征x和相应的实值标签y组成的训练数据，我们试图找到度数为d的多项式

$$y=\sum _{i=0}^d{W}^i{x}^i$$

这只是一个线性回归问题，我们的特征是由x的幂给出的，wi是由模型的权重给出的，而偏差是由w0给出的，因为x 0 = 1为所有x。高阶多项式函数比低阶多项式函数更复杂，因为高阶多项式有更多的参数，模型函数的选择范围也更广。固定训练数据集，相对于低阶多项式，高阶多项式函数应该总是能达到较低（最差也是相等）的训练误差。事实上，只要数据点都有一个不同的x值，度数等于数据点数量的多项式函数就能完全适合训练集。我们将多项式程度和欠拟合与过拟合之间的关系可视化如下。

二、数据集大小

要记住的另一个重要考虑因素是数据集的大小。固定我们的模型，我们在训练数据集中的样本越少，我们就越有可能（也越严重）遇到过拟合的问题。随着我们增加训练数据量，泛化误差通常会减少。此外，一般来说，更多的数据永远不会有坏处。对于一个固定的任务和数据分布，模型的复杂性和数据集的大小之间通常存在着一种关系。

如果有更多的数据，我们可能会尝试拟合一个更复杂的模型，这样做是有利的。如果没有足够的数据，较简单的模型可能很难被打败。对于许多任务，深度学习只有在有成千上万的训练实例时才会胜过线性模型。在某种程度上，深度学习目前的成功要归功于目前由于互联网公司、廉价存储、连接设备和经济的广泛数字化而带来的大量数据集。

三、多项式回归

现在我们可以通过对数据进行多项式拟合来交互地探索这些概念。为了开始，我们将导入我们常用的包。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as Data
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
from matplotlib import pyplot as plt

四、生成数据集

首先我们需要数据。给定x，我们将使用下面的三次方多项式来生成训练和测试数据的标签：

$$y=5+1.2x-3.4\frac{x^2}{2!}+5.6\frac{x^3}{3!}+EwhereE-N(0,0.1)$$

噪声项ϵ服从正态分布，平均值为0，标准差为0.1。我们将为训练集和测试集各合成100个样本

max_degree=20
n_train,n_test=100,100

poly_features=torch.zeros(20,200)
true_w=torch.zeros(max_degree)
true_w[0:4] = torch.tensor([5, 1.2, -3.4, 5.6])
features = torch.randn(size=(n_train + n_test, 1))
print(len(features))
print('features_sample:',features[1:5])

200
features_sample: tensor([[ 0.2953],
        [ 0.1419],
        [ 2.3510],
        [-0.3489]])

torch.pow(input, exponent, *, out=None) → Tensor

计算两个张量或者一个张量与一个标量的指数计算结果，返回一个张量。

input和exponent都可以是张量或者标量,

1)若input和exponent都为张量，则必须维度一致；

2)若input和exponent其中一个为标量，一个为张量，标量以广播的形式进行计算

poly_features=torch.zeros(20,200)
true_w=torch.zeros(max_degree)
true_w[0:4] = torch.tensor([5, 1.2, -3.4, 5.6])
features = torch.randn(size=(n_train + n_test, 1))
# 此时len(features)=200
x_list=torch.arange(max_degree)  
# torch.arange(max_degree)生成0-max_degree-1的张量
# 如tensor([ 0,  1,  2, ..., 16, 17,18, 19])
x_list.float()
features=features.reshape(1,-1)
# 在神经网络的语义里，一组特征值对应一个标签。所以要加上reshape(-1, 1)，让特征值和标签一一对应。
for i in range(1,max_degree):
    
    poly_features[i] = torch.pow(features,i)
    
print(features[:,3])
print(poly_features[:,3])

tensor([0.5201])
tensor([0.0000e+00, 5.2013e-01, 2.7053e-01, 1.4071e-01, 7.3188e-02, 3.8067e-02,
        1.9800e-02, 1.0298e-02, 5.3564e-03, 2.7860e-03, 1.4491e-03, 7.5371e-04,
        3.9203e-04, 2.0390e-04, 1.0606e-04, 5.5163e-05, 2.8692e-05, 1.4923e-05,
        7.7620e-06, 4.0372e-06])

poly_featrues的维度与max_degree一致。

对于优化来说，我们通常希望避免梯度、损失等的非常大的数值。这就是为什么存储在poly_features中的单项式是由x重新缩放的。

它使我们能够避免大指数i的非常大的值。因数在Gluon中使用Gamma函数实现，其中n！=Γ（n+b 1）。看一下生成的数据集的前2个样本。严格来说，数值1是一个特征，即对应于偏置的常数特征

from scipy.special import factorial
ok=torch.arange(1,(max_degree) + 1).reshape((1, -1))
import numpy as np
dr=np.array(factorial(ok))
dr2=torch.from_numpy(dr)
poly_features = poly_features.double() /dr2.t()
labels = torch.matmul(true_w.double(),poly_features)
poly_features = poly_features.type(torch.FloatTensor)
labels = labels.type(torch.FloatTensor)
labels += torch.randn(200)*0.5

print('label:',labels[1:3])
print('poly_features:',poly_features[1:3])

label: tensor([-1.1956,  0.1997])
poly_features: tensor([[-3.1400e-01, -2.3480e-01, -4.6314e-01,  2.6006e-01,  1.0187e+00,
         -6.9830e-01,  4.4445e-01, -8.6985e-01,  1.0671e-01,  1.1793e+00,
         -5.5948e-01, -2.8550e-01,  3.8387e-01,  7.8964e-01, -5.4954e-01,
         -6.2641e-01,  4.0432e-01, -2.6746e-01,  7.9382e-01,  1.3878e-01,
          1.8964e-02, -3.0917e-01,  3.7844e-01,  1.1040e+00, -5.0291e-01,
         -3.3822e-01,  3.0181e-01,  9.0185e-02,  7.2134e-01, -1.6417e-02,
          1.6719e-02, -2.0597e-02,  3.8049e-01,  7.3728e-01, -4.7587e-01,
          2.5029e-01, -3.6972e-01,  2.7229e-01,  6.7817e-01, -4.5840e-01,
         -1.0192e-01,  4.4336e-01, -8.6498e-01, -6.6167e-01, -7.3390e-01,
         -3.1954e-02, -2.5319e-01, -3.1537e-01,  5.3046e-02,  3.3482e-01,
         -4.3939e-01,  1.0898e-01,  2.6033e-01, -1.5160e+00,  5.4289e-01,
          1.6894e-01,  8.1840e-02,  2.2017e-01,  4.0803e-01,  1.0349e+00,
          2.5141e-02,  4.1763e-01,  3.0520e-01, -3.4512e-01, -4.4098e-01,
         -2.4226e-01, -1.2120e-01,  3.4511e-01, -6.5298e-01, -1.6932e-03,
         -2.0895e-01, -6.9718e-01,  3.5759e-01,  3.5523e-01,  5.6842e-01,
         -1.7945e-02,  4.2711e-01, -5.7841e-01,  6.9256e-01, -1.7349e-01,
         -5.1058e-01,  5.0590e-02,  9.6669e-01,  8.3027e-01, -1.9242e-01,
          4.8091e-02, -5.8907e-01,  4.9107e-01,  4.3220e-01,  3.8178e-01,
         -2.1670e-02, -3.4599e-01, -8.0641e-01, -4.8481e-01,  4.6595e-01,
         -7.0008e-01, -1.6731e-01,  3.0853e-01, -2.0891e-01,  5.0182e-02,
         -6.8278e-01, -6.2210e-01,  2.6816e-01,  3.2911e-01,  3.2188e-02,
          2.6063e-01, -5.5399e-01, -4.2825e-01,  1.0510e+00,  3.7201e-01,
         -5.1389e-01,  5.5163e-01, -5.8923e-03,  1.2088e+00,  2.1583e-01,
          2.5300e-02, -7.1968e-01, -2.5226e-01, -5.4693e-01, -2.1076e-01,
          1.0129e-01, -1.4640e-01, -1.4477e-01,  5.2616e-01, -9.1825e-01,
          2.2752e-01,  5.7931e-01,  8.6443e-02, -1.9949e-01,  4.5472e-01,
         -1.0476e-01,  5.5642e-01, -6.1096e-01, -1.2485e-01,  6.6338e-01,
          9.2693e-02,  2.3368e-01,  3.4167e-01, -2.7173e-01,  8.4498e-01,
         -6.6640e-01,  6.0106e-01, -2.6324e-02, -6.5853e-02,  3.2732e-01,
          1.5165e-01,  5.2006e-01, -3.5379e-01,  6.1084e-02, -1.7663e-01,
          2.6346e-01, -5.1887e-01,  8.1525e-01, -8.9162e-01,  3.8223e-01,
          3.3044e-01,  4.8643e-03,  2.4476e-01, -2.9402e-01, -6.6403e-01,
         -5.7634e-01, -1.8108e-01,  3.4945e-01, -9.2972e-02,  2.6097e-01,
         -1.7739e-01,  4.4916e-01, -4.5783e-02, -5.6727e-01,  2.0923e-01,
          2.1904e-01,  8.1564e-01, -4.3642e-03,  5.0278e-01, -3.0945e-01,
         -5.2889e-01,  2.4982e-01,  8.0057e-01,  3.4643e-01, -1.0574e+00,
          3.2641e-01,  5.3184e-01, -3.5789e-01, -5.8631e-01, -1.8255e-02,
          5.2955e-01, -8.6759e-01, -1.6631e-01,  3.9272e-01,  3.0628e-01,
          9.9851e-01, -8.6854e-01,  5.3226e-01,  9.8750e-03,  6.3992e-01,
          7.8651e-01,  2.6739e-02,  4.5857e-02,  3.1480e-01, -4.6563e-01],
        [ 6.5731e-02,  3.6754e-02,  1.4300e-01,  4.5089e-02,  6.9182e-01,
          3.2509e-01,  1.3169e-01,  5.0443e-01,  7.5915e-03,  9.2720e-01,
          2.0868e-01,  5.4340e-02,  9.8239e-02,  4.1569e-01,  2.0133e-01,
          2.6160e-01,  1.0898e-01,  4.7689e-02,  4.2010e-01,  1.2840e-02,
          2.3975e-04,  6.3724e-02,  9.5478e-02,  8.1250e-01,  1.6862e-01,
          7.6262e-02,  6.0726e-02,  5.4222e-03,  3.4689e-01,  1.7968e-04,
          1.8636e-04,  2.8281e-04,  9.6513e-02,  3.6239e-01,  1.5097e-01,
          4.1764e-02,  9.1128e-02,  4.9429e-02,  3.0661e-01,  1.4009e-01,
          6.9252e-03,  1.3104e-01,  4.9879e-01,  2.9187e-01,  3.5907e-01,
          6.8071e-04,  4.2736e-02,  6.6305e-02,  1.8759e-03,  7.4734e-02,
          1.2871e-01,  7.9173e-03,  4.5180e-02,  1.5323e+00,  1.9649e-01,
          1.9028e-02,  4.4652e-03,  3.2317e-02,  1.1099e-01,  7.1396e-01,
          4.2138e-04,  1.1627e-01,  6.2099e-02,  7.9405e-02,  1.2964e-01,
          3.9126e-02,  9.7932e-03,  7.9399e-02,  2.8426e-01,  1.9112e-06,
          2.9106e-02,  3.2404e-01,  8.5246e-02,  8.4126e-02,  2.1540e-01,
          2.1469e-04,  1.2162e-01,  2.2304e-01,  3.1976e-01,  2.0066e-02,
          1.7379e-01,  1.7062e-03,  6.2300e-01,  4.5956e-01,  2.4685e-02,
          1.5418e-03,  2.3134e-01,  1.6077e-01,  1.2453e-01,  9.7172e-02,
          3.1305e-04,  7.9807e-02,  4.3353e-01,  1.5669e-01,  1.4474e-01,
          3.2674e-01,  1.8662e-02,  6.3460e-02,  2.9097e-02,  1.6788e-03,
          3.1079e-01,  2.5800e-01,  4.7940e-02,  7.2209e-02,  6.9073e-04,
          4.5286e-02,  2.0460e-01,  1.2227e-01,  7.3636e-01,  9.2261e-02,
          1.7605e-01,  2.0287e-01,  2.3146e-05,  9.7407e-01,  3.1056e-02,
          4.2672e-04,  3.4529e-01,  4.2425e-02,  1.9942e-01,  2.9612e-02,
          6.8402e-03,  1.4289e-02,  1.3973e-02,  1.8456e-01,  5.6212e-01,
          3.4510e-02,  2.2373e-01,  4.9815e-03,  2.6532e-02,  1.3784e-01,
          7.3169e-03,  2.0640e-01,  2.4884e-01,  1.0392e-02,  2.9338e-01,
          5.7280e-03,  3.6404e-02,  7.7824e-02,  4.9226e-02,  4.7599e-01,
          2.9606e-01,  2.4085e-01,  4.6198e-04,  2.8911e-03,  7.1426e-02,
          1.5332e-02,  1.8031e-01,  8.3446e-02,  2.4875e-03,  2.0799e-02,
          4.6274e-02,  1.7948e-01,  4.4309e-01,  5.2999e-01,  9.7400e-02,
          7.2794e-02,  1.5774e-05,  3.9939e-02,  5.7630e-02,  2.9396e-01,
          2.2145e-01,  2.1859e-02,  8.1412e-02,  5.7625e-03,  4.5405e-02,
          2.0978e-02,  1.3449e-01,  1.3974e-03,  2.1453e-01,  2.9184e-02,
          3.1986e-02,  4.4351e-01,  1.2697e-05,  1.6853e-01,  6.3838e-02,
          1.8648e-01,  4.1606e-02,  4.2727e-01,  8.0008e-02,  7.4544e-01,
          7.1029e-02,  1.8857e-01,  8.5389e-02,  2.2917e-01,  2.2215e-04,
          1.8695e-01,  5.0181e-01,  1.8439e-02,  1.0282e-01,  6.2539e-02,
          6.6468e-01,  5.0291e-01,  1.8887e-01,  6.5010e-05,  2.7300e-01,
          4.1240e-01,  4.7665e-04,  1.4019e-03,  6.6065e-02,  1.4454e-01]])

五、定义、训练和测试模型

我们首先定义绘图函数emilogy，其中y轴利用了对数尺度

由于我们将尝试使用不同复杂度的模型来拟合生成的数据集，我们将模型定义插入fit_and_plot函数中。多项式函数拟合中涉及的训练和测试步骤与之前描述的softmax回归相似

def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
legend=None, figsize=(3.5, 2.5)):
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.semilogy(x_vals, y_vals)
    if x2_vals and y2_vals:
        plt.semilogy(x2_vals, y2_vals, linestyle=':')
        plt.legend(legend)

def fit_and_plot(train_features,train_labels,test_features,test_labels,no_inputs):
    class LinearRegressionModel(torch.nn.Module): 
  
        def __init__(self): 
            super(LinearRegressionModel, self).__init__() 
            self.linear = torch.nn.Linear(no_inputs, 1)  
  
        def forward(self, x): 
            y_pred = self.linear(x) 
            return y_pred 

    model = LinearRegressionModel() 
    criterion = torch.nn.MSELoss(reduction='sum') 
    optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)
    train_ls,test_ls=[],[]
    train_labels=train_labels.reshape(-1,1)
    train_ds=TensorDataset(train_features,train_labels)
    batch_size=10
    train_dl=DataLoader(train_ds,batch_size,shuffle=True)
    test_labels=test_labels.reshape(-1,1)
    for ep in range(100):
        for xb,yb in train_dl: 
            pred_y = model(xb) 
            loss = criterion(pred_y, yb) 
            optimizer.zero_grad() 
            loss.backward() 
            optimizer.step()
        predytr=model(train_features)
        train_ls.append((criterion(predytr,train_labels)).mean())
        predyts=model(test_features)
        test_ls.append((criterion(predyts,test_labels)).mean())    
    print('final epoch:train loss',train_ls[-1],'test Loss',test_ls[-1])
    semilogy(range(1,ep+2), train_ls,'epoch','loss',range(1,ep+2),test_ls,['train','test'])

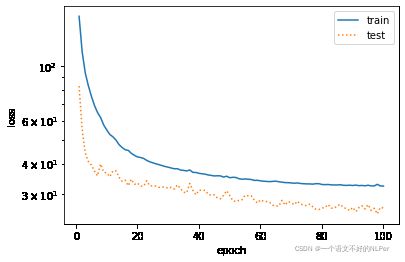
六、三阶多项式函数拟合(正常情况)

我们首先使用一个与数据生成函数同阶的三阶多项式函数。结果显示，在使用测试数据集时，这个模型的训练错误率很低。训练后的模型参数也接近于真实值w = [5, 1.2, -3.4, 5.6]。

poly_features_t=poly_features.t()
fit_and_plot(train_features=poly_features_t[:100,0:4],train_labels=labels[:100],test_features=poly_features_t[100:,0:4],test_labels=labels[100:],no_inputs=4)

final epoch:train loss tensor(32.4263, grad_fn=) test Loss tensor(26.4059, grad_fn=)

七、线性函数拟合（欠拟合）

让我们再看一下线性函数拟合。在早期 epoch 的下降之后，进一步降低这个模型的训练错误率变得很困难。在最后一个 epoch 迭代完成后，训练错误率仍然很高。当用于拟合非线性模式（如这里的三阶多项式函数）时，线性模型容易出现欠拟合。

fit_and_plot(train_features=poly_features_t[:100,0:3],train_labels=labels[:100],test_features=poly_features_t[100:,0:3],test_labels=labels[100:],no_inputs=3)

final epoch:train loss tensor(64.4643, grad_fn=) test Loss tensor(53.6851, grad_fn=)

八、训练过拟合

现在让我们尝试用一个度数过高的多项式来训练这个模型。这里，没有足够的数据来学习高阶系数应该有接近零的值。因此，我们过于复杂的模型太容易受到训练数据中噪音的影响了。当然，我们的训练误差现在会很低（甚至比我们有正确的模型还低！），但我们的测试误差会很高。尝试不同的模型复杂度（n_degree）和训练集大小（n_subset），以获得一些对所发生情况的直觉。

fit_and_plot(train_features=poly_features_t[1:100,0:20],train_labels=labels[1:100],test_features=poly_features_t[100:,0:20],test_labels=labels[100:],no_inputs=20)

final epoch:train loss tensor(32.3802, grad_fn=) test Loss tensor(26.4659, grad_fn=)

九、总结

• 由于泛化错误率不能根据训练错误率来估计，简单地将训练错误率最小化并不一定意味着泛化错误率的降低。机器学习模型需要注意防止过度拟合，从而使泛化误差最小化。

• 验证集可以用于模型的选择（前提是不能用得太随意）。

• 欠拟合意味着模型无法降低训练错误率，而过拟合是指模型训练错误率远远低于测试数据集的错误率。

• 我们应该选择一个适当的复杂模型，避免使用不充分的训练样本

十、练习题

1、你能准确解决多项式回归问题吗？提示 - 使用线性代数。

2、多项式的模型选择

• 绘制训练误差与模型复杂性（多项式的度数）的关系图。你观察到了什么？

• 画出这种情况下的测试误差。

• 生成相同的数据量的函数图？

3、如果你放弃对多项式特征x i的归一化，用1/i！会发生什么？你能以其他方式解决这个问题吗？

4、你需要多少度的多项式才能将训练误差降低到0？