基于改进SEIR模型的病毒传播动力学建模与疫情预测分析(以COVID-19新冠病毒为例,超详细,带matlab源码)
文章目录
- 前言
- 一、数学基础知识
-
- 符号定义
- 二、传统SEIR模型的建立与求解
-
- 1.经典的SEIR传播动力学模型建立
- 2.根据经典的SEIR模型列出微分方程并求解
- 三、SEIR模型第一次修正
-
- 1.模型建立
- 2.模型求解
- 四、SEIR模型的第二次修正
-
- 1.模型建立
- 2.模型求解
- 五、SEIR模型的第三次修正
-
- 1.模型建立
- 2.模型求解
- 六、模型检验
- 七、总结
前言
SEIR模型是现在较为成熟流行病预测模型,所研究的传染病具有一定时间的潜伏期,与患者接触的正常人并不会马上患病,而是成为病原体的携带者。
传统的SEIR模型包含五大部分,即易感染者、潜伏者、患病者、康复者。
本文多次改进了传统的SEIR模型,引入了死亡者、医疗隔离者、自我隔离者,使得模型更加完备准确。
最终,模型的预测结果在5月7日前后总感染者达到了80,000人左右,与实际数据仅相差不到2000人。
一、数学基础知识
马尔可夫链
微分方程
符号定义
| 符号 | 单位 | 意义 |
|---|---|---|
| N | 人 | 总人数 |
| S | 人 | 易感染者 |
| E | 人 | 潜伏者 |
| I | 人 | 感染者 |
| R | 人 | 康复者 |
| D | 人 | 死亡者 |
| F | 人 | 自我隔离者 |
| Q | 人 | 医疗隔离者 |
| h | 常数 | 传播系数 |
| a | 常数 | 接触人数 |
| b | 常数 | 感染率 |
| k | 常数 | 感染者死亡率 |
| f | 常数 | 自我隔离速率 |
| q | 常数 | 医疗隔离速率 |
| r | 常数 | 感染者康复率 |
| r_1 | 常数 | 隔离者康复率 |
| k_1 | 常数 | 隔离者死亡率 |
| c | 常数 | 潜伏者转阴率 |
| i | 常数 | 转病率 |
二、传统SEIR模型的建立与求解
1.经典的SEIR传播动力学模型建立
在建立经典SEIR模型时,我们同时引入死亡者。
要建立经典SEIR传播动力学模型,需要将人类群体分为五大部分(易感染者、潜伏者、患病者、康复者、死亡者),各个部分人群未来趋势走向具有相互转化的可能。
其中,人群相互转化存在一定的比率关系,建立的关于各个部分人群未来趋势走向的SEIR传播动力学模型如下。

2.根据经典的SEIR模型列出微分方程并求解
在新冠病毒传染病蔓延过程中,各部分人群未来趋势走向是按照一定的比率进行转化的。因此,根据上图经典的SEIR传播动力学模型构建微分方程。
d S / d t = − h I S / N \mathrm{dS/dt=-}hIS/N dS/dt=−hIS/N d E / d t = h I S / N − i E \mathrm{dE/dt=}hIS/N-iE dE/dt=hIS/N−iE d I / d t = i E − r I − k I \mathrm{dI/dt=iE}-rI-kI dI/dt=iE−rI−kI d R / d t = r I dR/\mathrm{dt}=rI dR/dt=rI d D / d t = k I dD/dt=kI dD/dt=kI
将其看做马可夫链,我们假设后一天的状态只与前一天状态有关,故推出以下迭代方程。
S n + 1 = S n − h I n S n / N S_{n+1}=S_n-hI_nS_n/N Sn+1=Sn−hInSn/N E n + 1 = E n + h I n S n / N − i E n E_{n+1}=E_n+hI_nS_n/N-iE_n En+1=En+hInSn/N−iEn I n + 1 = I n + i E n − r I n − k I n I_{n+1}=I_n+iE_n-rI_n-kI_n In+1=In+iEn−rIn−kIn R n + 1 = R n + r I n R_{n+1}=R_n+rI_n Rn+1=Rn+rIn D n + 1 = D n + k I n D_{n+1}=D_n+kI_n Dn+1=Dn+kIn
以我国数据为例,我们取a=20,b=0.03,最终得出传播系数h=0.6(以SARS为标准),转病率i=0.125(潜伏期为2-14天,故取1/8),康复率r=0.1,感染者死亡率k=0.05,将参数带入迭代方程并使用MATLAB求解得出如下结果。

由上图可见,日最大存在的感染者达到了250,000,000左右,与实际的数据严重不符,这是因为经典的SEIR模型只考虑了无限制传播的情况,所以在后面我们将对经典模型进行进一步改进。
代码
%SEIR模型求解
clear;clc;
%参数设置
N = 1400000000;%人口数
I = 1;%传染者
R = 0;%康复者
D = 0;%死亡患者数量
E = 0;%潜伏者
S = N-I;%易感染者
a = 20;%感染者平均接触人数
b = 0.03;%感染率
h = a*b;%感染系数(以SARS为准)
i = 0.125;%潜伏者患病概率
r = 0.1;%康复概率
k = 0.05;%死亡概率
T = 1:500;
for idx =1:length(T)-1
S(idx+1)=S(idx)-h*I(idx)*S(idx)/N;%易感人数迭代
E(idx+1)=E(idx)+h*S(idx)*I(idx)/N-i*E(idx);%潜伏者人数迭代
I(idx+1)=I(idx)+i*E(idx)-(r+k)*I(idx);%患病人数迭代
R(idx+1)=R(idx)+r*I(idx);%康复人数迭代
D(idx+1)=D(idx)+k*I(idx);%死亡患者人数迭代
end
plot(T,S,T,E,T,I,T,R,T,D);
grid on;
xlabel('日期');
ylabel('人数');
legend('易感者','潜伏者','感染者','康复者','死亡者');
title('SEIR模型');
三、SEIR模型第一次修正
1.模型建立
修正思路:由于此次新冠肺炎有未发病感染症状,故患者在潜伏阶段也会感染正常人,所以我们引入潜伏者感染系数h_1。
同时,潜伏者还存在自愈转阴的情况,所以,同时引入潜伏者转阴率c。
建模如下

2.模型求解
通过SEIR模型,我们可以得到如下微分方程:
d S / d t = − h I S / N − h 1 E S / N + c E \mathrm{dS/dt=}-hIS/N-h_1ES/N+cE dS/dt=−hIS/N−h1ES/N+cE d E / d t = h I S / N + h 1 E S / N − i E − c E \mathrm{dE/dt=}hIS/N{+h}_1ES/N-iE-cE dE/dt=hIS/N+h1ES/N−iE−cE d I / d t = i E − r I − k I \mathrm{dI/dt=iE}-rI-kI dI/dt=iE−rI−kI d R / d t = r I dR/dt=rI dR/dt=rI d D / d t = k I dD/dt=kI dD/dt=kI
根据上述微分方程推出以下迭代方程:
S n + 1 = S n − h I n S n / N − h 1 I n S n / N + c E n S_{n+1}=S_n-hI_nS_n/N-{h_1I}_nS_n/N+cE_n Sn+1=Sn−hInSn/N−h1InSn/N+cEn E n + 1 = E n + h I n S n / N − i E n − c E n E_{n+1}=E_n+hI_nS_n/N-iE_n-cE_n En+1=En+hInSn/N−iEn−cEn I n + 1 = I n + i E n − r I n − k I n I_{n+1}=I_n+iE_n-rI_n-kI_n In+1=In+iEn−rIn−kIn R n + 1 = R n + r I n R_{n+1}=R_n+rI_n Rn+1=Rn+rIn D n + 1 = D n + k I n D_{n+1}=D_n+kI_n Dn+1=Dn+kIn
在原参数的基础上,取潜伏者感染系数h_1与感染者感染系数h相同,转阴率c=0.05。将参数代入第一次修正的SEIR模型,使用MATLAB求解,结果如下。

可以看到,引入潜伏者感染系数后,感染者大幅上升,爆发速度也更快,更加接近新冠病毒疫情的实际效果。
四、SEIR模型的第二次修正
1.模型建立
修正思路:由于我国的快速响应,采取了定点医院隔离措施,积极收治感染者,故引入新的人群医疗隔离者Q,感染者被收治的速率为q,由于医院医疗条件较好,故医疗隔离者死亡率k_1与隔离者治愈率r_1应单独考虑。由于患者被严格隔离,所以其不具备传染性。
第二次修正后SEIR模型如下:

2.模型求解
通过SEIR模型,我们得到如下微分方程:
d S / d t = − h I S / N − h 1 E S / N + c E \mathrm{dS/dt=}-hIS/N-h_1ES/N+cE dS/dt=−hIS/N−h1ES/N+cE d E / d t = h I S / N + h 1 E S / N − i E − c E \mathrm{dE/dt=}hIS/N{+h}_1ES/N-iE-cE dE/dt=hIS/N+h1ES/N−iE−cE d I / d t = i E − r I − k I − q I \mathrm{dI/dt=iE}-rI-kI-qI dI/dt=iE−rI−kI−qI d R / d t = r I + r 1 Q dR/dt=rI+r_1Q dR/dt=rI+r1Q d D / d t = k I + k 1 Q dD/dt=kI+k_1Q dD/dt=kI+k1Q d Q / d t = q I − r 1 Q − k 1 Q dQ/dt=\ qI-r_1Q-k_1Q dQ/dt= qI−r1Q−k1Q
根据上述微分方程推出以下迭代方程:
S n + 1 = S n − h I n S n / N − h 1 I n S n / N + c E n S_{n+1}=S_n-hI_nS_n/N-{h_1I}_nS_n/N+cE_n Sn+1=Sn−hInSn/N−h1InSn/N+cEn E n + 1 = E n + h I n S n / N − i E n − c E n E_{n+1}=E_n+hI_nS_n/N-iE_n-cE_n En+1=En+hInSn/N−iEn−cEn I n + 1 = I n + i E n − r I n − k I n − q I n I_{n+1}=I_n+iE_n-rI_n-kI_n-{\rm qI}_n In+1=In+iEn−rIn−kIn−qIn R n + 1 = R n + r I n + r 1 Q n R_{n+1}=R_n+rI_n+r_1Q_n Rn+1=Rn+rIn+r1Qn D n + 1 = D n + k I n + k 1 Q n D_{n+1}=D_n+kI_n+k_1Q_n Dn+1=Dn+kIn+k1Qn Q n + 1 = q I n − r 1 Q n − k 1 Q n Q_{n+1}={\rm qI}_n-r_1Q_n-k_1Q_n Qn+1=qIn−r1Qn−k1Qn
由于我国响应快速,医疗措施较好,故取q=0.9,r_1=1.2r, k_1=0.05k。
在原参数的基础上,将上述参数代入第二次修正的SEIR模型,并使用MATLAB求解,结果如下图所示。

虽然日存在感染人数有所下降,可是几乎所有样本都被感染,最高日存在感染人数高达3.5亿(感染者与潜伏者的总数,即为总携带者),仍偏离实际。这是因为在动态的转化中,所有的易感染者都处于不受保护的状态,最终都会变成感染者或潜伏者。
此时的模型虽然定量分析偏离实际,但是定性来说,很好的符合了我国新冠肺炎疫情的情况,感染人数首先以指数增加,此时是病毒的爬升期;在数十天后达到峰值,迎来拐点;随后缓慢下降直到清零,治愈人数与死亡人数也同时趋于稳定。
五、SEIR模型的第三次修正
1.模型建立
由于我国处理措施得当,及时进行了管制措施,使得感染者与潜伏者日接触人数a大幅下降,所以模型在采取管制措施后应当下调传染系数h。
此外,由于民众自我隔离,每天都有易感染者S成为不易感染的自我隔离者F,其速率为f。现假设易感染者成为自我隔离者后绝对安全,不会被感染。
第三次修正后SEIR模型如下。
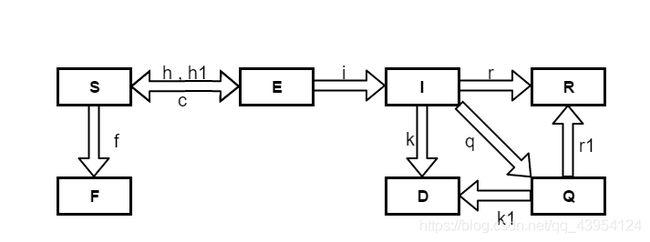
2.模型求解
由以上SEIR模型可得以下微分方程:
d E / d t = h I S / N + h 1 E S / N − i E − c E \mathrm{dE/dt=}hIS/N{+h}_1ES/N-iE-cE dE/dt=hIS/N+h1ES/N−iE−cE d I / d t = i E − r I − k I − q I \mathrm{dI/dt=iE}-rI-kI-qI dI/dt=iE−rI−kI−qI d R / d t = r I + r 1 Q dR/dt=rI+r_1Q dR/dt=rI+r1Q d D / d t = k I + k 1 Q dD/dt=kI+k_1Q dD/dt=kI+k1Q d Q / d t = q I − r 1 Q − k 1 Q dQ/dt=\ qI-r_1Q-k_1Q dQ/dt= qI−r1Q−k1Q
当没有采取管制措施时:
d S / d t = − h I S / N − h 1 E S / N + c E \mathrm{dS/dt=}-hIS/N-h_1ES/N+cE dS/dt=−hIS/N−h1ES/N+cE
当采取管制措施时:
d S / d t = − h I S / N − h 1 E S / N + c E − f S \mathrm{dS/dt=}-hIS/N-h_1ES/N+cE-fS dS/dt=−hIS/N−h1ES/N+cE−fS
由于自我隔离者不会被感染,所以不用计算其人数。由以上微分方程可得以下迭代方程:
E n + 1 = E n + h I n S n / N − i E n − c E n E_{n+1}=E_n+hI_nS_n/N-iE_n-cE_n En+1=En+hInSn/N−iEn−cEn I n + 1 = I n + i E n − r I n − k I n − q I n I_{n+1}=I_n+iE_n-rI_n-kI_n-{\rm qI}_n In+1=In+iEn−rIn−kIn−qIn R n + 1 = R n + r I n + r 1 Q n R_{n+1}=R_n+rI_n+r_1Q_n Rn+1=Rn+rIn+r1Qn D n + 1 = D n + k I n + k 1 Q n D_{n+1}=D_n+kI_n+k_1Q_n Dn+1=Dn+kIn+k1Qn Q n + 1 = q I n − r 1 Q n − k 1 Q n Q_{n+1}={\rm qI}_n-r_1Q_n-k_1Q_n Qn+1=qIn−r1Qn−k1Qn
当没有采取管制措施时:
S n + 1 = S n − h I n S n / N − h 1 I n S n / N + c E n S_{n+1}=S_n-hI_nS_n/N-{h_1I}_nS_n/N+cE_n Sn+1=Sn−hInSn/N−h1InSn/N+cEn
当采取管制措施时:
S n + 1 = S n − h I n S n / N − h 1 I n S n / N + c E n − f S n S_{n+1}=S_n-hI_nS_n/N-{h_1I}_nS_n/N+cE_n-fS_n Sn+1=Sn−hInSn/N−h1InSn/N+cEn−fSn
根据我国情况,我们取a=5,f=0.3,在第31天采取管制措施。在原参数基础上,将以上参数代入第三次修正的模型,并使用MATLAB求解,结果如下。

可以看到,SEIR模型经过改进后,日存在患者人数最高达到32000(感染者与潜伏者的总数,即为总携带者),总患病人数达到约80000,与我国数据极为接近。
代码
%SEIR模型第三次修正,易感人群进行自我隔离
clear;clc;
%参数设置
N=1400000000;%人口数
%参数设置
N=1400000000;%人口数
I = 1;%传染者
R = 0;%康复者
D = 0;%死亡患者数量
E = 0;%潜伏者
S = N-I;%易感染者
Q = 0;%隔离者人数
Iq = I+Q;%现存总患病人数
F = 0;%自我隔离人数
sum_I = 1;%累计感染人数
a = 20;%感染者平均每日接触人数
b = 0.03;%平均感染率
h = a*b;%传染系数(以SARS为标准)
i = 0.125;%潜伏者患病概率
r = 0.1;%康复概率
k = 0.05;%死亡概率
r1 =r*1.15;%隔离者治愈率
q = 0.9;%隔离速率
d1 = k*0.05;%隔离者死亡率
f = 0.3;%自我隔离速率
day=31;%采取控制措施的天数
c = 0.05;%转阴率
T = 1:200;
for idx = 1:length(T)-1
S(idx+1) = S(idx)-h*I(idx)*S(idx)/N-h*E(idx)*S(idx)/N+c*E(idx);%易感人数迭代
E(idx+1) = E(idx)+h*I(idx)*S(idx)/N+h*E(idx)*S(idx)/N-i*E(idx)-c*E(idx);%潜伏者人数迭代
I(idx+1) = I(idx)+i*E(idx)-(r+k)*I(idx)-q*I(idx);%患病人数迭代
R(idx+1) = R(idx)+r*I(idx)+r1*Q(idx);%康复人数迭代
D(idx+1) = D(idx)+k*I(idx)+d1*Q(idx);%死亡患者人数迭代
Q(idx+1) = Q(idx)+q*I(idx)-r1*Q(idx)-d1*Q(idx);%隔离人数迭代
Iq(idx+1) = I(idx)+Q(idx);%现存总患病人数迭代
if idx == day
a = 5;%采取控制措施后感染者平均接触人数
h = a*b;%采取控制措施后感染系数
end
if idx>=day
S(idx+1) = S(idx)-f*S(idx);%采取控制措施后潜伏者人数迭代
end
sum_I(idx+1) = sum_I(idx) + i*E(idx);%累计患病人数迭代(累计患病人数=前一天的患病人数+新增患病)
end
plot(T,E,T,I,T,R,T,D,T,Iq,T,sum_I);
grid on;
xlabel('日期');
ylabel('人数');
legend('潜伏者','感染者','康复者','死亡者','总感染人数','累计感染人数');
title('SEIR模型第三次修正');
六、模型检验
带入上面的参数,将结果与国内实际情况对比
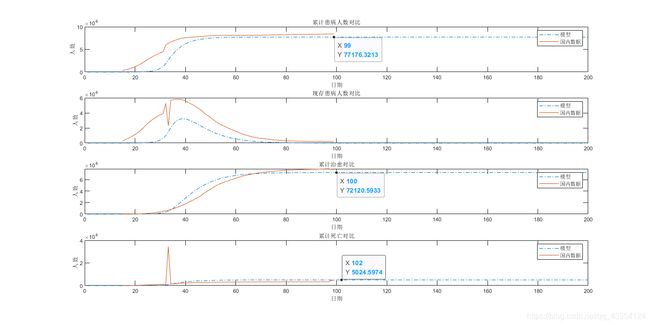
可以看出,模型成功预测了爆发时间(19年12月前后),拐点的到达时间,最终的总感染人数,总死亡人数,总治愈人数等。
修改参数,与美国实际情况对比
使N=330000000,转病率i=0.1,康复率r=0.09,死亡率k=0.02,医疗隔离速率q=0.2,自我隔离速率f=0.005,在第29天采取管制措施,其余参数与上面一致。

以上数据均截止至5月7日
七、总结
优点:该模型预测最终患病人数、最终死亡人数、拐点时间较为准确,可以准确判断疫情带来的影响。不但如此,模型可以根据数据估算出当前已经携带病毒的总人数(感染者与潜伏者的总数),由此可以进一步确定应对措施。
缺点:该趋势预测模型由于考虑的参数比较多,所以会存在一定的计算误差。而且由于对疫情考虑过于理想,所以对日存在患者数的预测不是特别准确。