【数据结构】——八大排序
文章目录
-
-
- 1.插入排序
- 2.冒泡排序
- 3.希尔排序
- 4.选择排序
- 5.快速排序
-
- 快排优化
- 递归改非递归
- 6.堆排序
- 7.归并排序
-
- 递归归并排序
- 改成非递归
- 8.计数排序
- 9.题目
-
- 总结:排序的时间检验
-

1.插入排序
void InsertSort(int* a, int n)
{
//i的最大下标为n-2,
for(int i=0;i<n-1;i++)
{
//下标为end+1的元素是每次循环需要排序的元素
int end=i;
int tmp=a[end+1];
while(end>=0)
{
if(tmp<a[end])
{
a[end+1]=a[end];
--end;
}
else
{
break;
}
}
a[end+1]=tmp;
}
}
时间复杂度:O(n^2)
2.冒泡排序
void Swap(int* pa, int* pb)
{
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; ++j)
{
int exchange = 0;
// 单趟
for (int i = 1; i < n-j; ++i)
{
if (a[i - 1] > a[i])
{
exchange = 1;
Swap(&a[i - 1], &a[i]);
}
}
if (exchange == 0)
{
break;
}
}
}
时间复杂度:O(n^2)
3.希尔排序
特点
gap越小,越有序
gap越大,最大多数越在后面,越小的数越在前面,但是越无序
3.1一般希尔排序
void ShellSort(int*a,int n)
{
for(int j=0;j<gap;j++)
{
//步长为gap
for(int i=j;i<n-gap;i+=gap)
{
//单躺希尔排序
int i=end;
int tmp=a[end+gap];
while(end>=0)
{
if(tmp<a[end])
{
a[end+gap]=a[end];
end-=gap;
}
else
{
break;
}
}
a[end+gap]=tmp;-
}
}
}
3.2改进的希尔排序
多组同时进行预排序
void ShellSort(int*a,int n)
{
int gap=n;
while(gap>1)
{
gap=gap/3+1;
//多组同时进行预排序
for(int i=0;i<n-gap;i++)
{
int end=i;
int tmp=a[end+gap];
while(end>=0)
{
if(tmp<a[end])
{
a[end+gap]=a[end];
end-=gap;
}
else
{
break;
}
}
a[end+gap]=tmp;
}
}
}
4.选择排序
void SelectSort(int*a,int n)
{
int left=0,right=n-1;
while(left<right)
{
int mini=left,maxi=left;
for(int i=left+1;i<=right;i++)
{
if(a[i]<a[mini]) mini=i;
if(a[i]>a[maxi]) maxi=i;
}
Swap(&a[mini],&a[left]);
if(maxi==left)
{
maxi=mini;
}
Swap(&a[maxi],&a[right]);
left++;
right--;
}
}
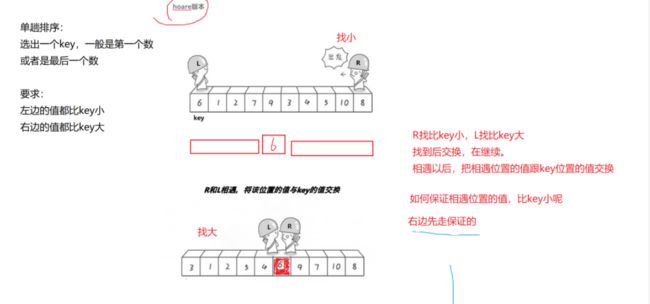
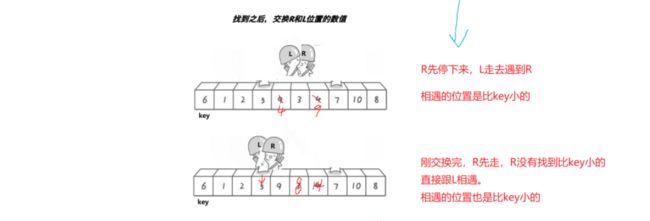
5.快速排序
算法实现:
左边做key,就右边先走
右边做key,就左边先走
//先进行每一趟的排序
int PartSort1(int*a,int left,int right)
{
int key=left;
while(left<right)
{
//右边先走
while(left<right&&a[right]>=a[key]) right--;
while(left<right&&a[left]<=a[key]) left++;
Swap(&a[left],&a[right]);
}
Swap(&a[key],&a[left]);
return left;
}
hoare递归快排
//模板一
void QuickSort(int*a,int begin,int end)
{
if(begin>=end)
return ;
//返回中间的值
int key=PartSort1(a,begin,end);
QuickSort(a,0,key-1);
QuickSort(a,key+1,end-1);
}
//模板二
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
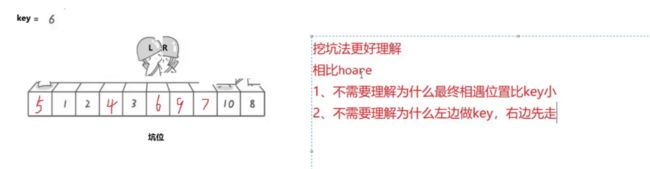
int PartSort2(int*a,int left,int right)
{
int key=a[left];
int pit=left;
while(left<right)
{
//先走右边
while(left<right&&a[right]>=key) right--;
a[pit]=a[right];
pit=right;
while(left<right&&a[left]>=key) left++;
a[pit]=a[left];
pit=left;
}
a[pit]=key;
return pit;
}
void QuickSort(int*a,int begin,int end)
{
if(begin>=end)
return ;
//返回中间的值
int key=PartSort2(a,begin,end);
QuickSort(a,0,key-1);
QuickSort(a,key+1,end-1);
}
int PartSort3(int* a, int left, int right)
{
int keyi = left;
int prev = left, cur = prev + 1;
while (cur<=right)
{
//遇见比自己小的就交换,同时避免不必要的交换
if (a[cur] <a[keyi]&&a[++prev]!=a[cur])
swap(&a[cur], &a[prev]);
cur++;
}
swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int*a,int begin,int end)
{
if(begin>=end)
return ;
//返回中间的值
int key=PartSort3(a,begin,end);
QuickSort3(a,0,key-1);
QuickSort3(a,key+1,end-1);
}
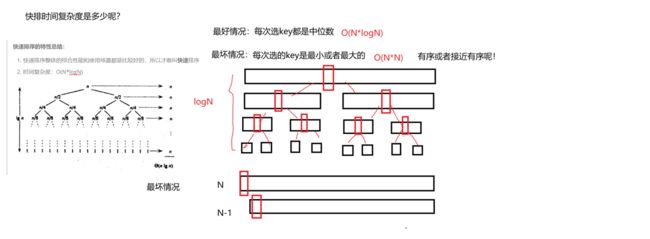
每次选出的key都是最大或最小,那么最坏的时间复杂度就是O(N^2)
快排优化
int GetMidIndex(int*a,int left,int right)
{
int mid=left+(right-left)/2;
if(a[left]>a[mid])
{
if(a[mid]<a[right]) return mid;
else if(a[left]>a[right]) return left;
else return right;
}
else
{
if(a[mid]>a[right]) return mid;
else if(a[left]<a[right]) return left;
else return right;
}
}
对于前后指针法的三数取中的优化法
int PartSort3(int* a, int left, int right)
{
int mid=GetMidIndex(a,left,right);
Swap(&a[mid],a[left]);
int keyi = left;
int prev = left, cur = prev + 1;
while (cur<=right)
{
//遇见比自己小的就交换,同时避免不必要的交换
if (a[cur] <a[keyi]&&a[++prev]!=a[cur])
swap(&a[cur], &a[prev]);
cur++;
}
swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int*a,int begin,int end)
{
if(begin>=end)
return ;
//返回中间的值
int key=PartSort3(a,begin,end);
QuickSort3(a,0,key-1);
QuickSort3(a,key+1,end-1);
}
2.小区间优化
在区间较小的时候,可以使用插入排序
int PartSort3(int* a, int left, int right)
{
int keyi = left;
int prev = left, cur = prev + 1;
while (cur<=right)
{
//遇见比自己小的就交换,同时避免不必要的交换
if (a[cur] <a[keyi]&&a[++prev]!=a[cur])
swap(&a[cur], &a[prev]);
cur++;
}
swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSort(int*a,int begin,int end)
{
if(begin>=end)
return ;
//返回中间的值
if(end-begin+1<=13)
{
InsertSort(a+begin,end-begin+1)
}
else
{
int key=PartSort3(a,begin,end);
QuickSort(a,0,key-1);
QuickSort(a,key+1,end-1);
}
}
递归改非递归
//递归在栈区调用,容易出现爆栈的风险,所以使用数据结构栈改为非递归
//使用栈,在堆上面开辟空间
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (StackEmpty(&st) != 0)
{
right = StackTop(&st);
StackPop(&st);
left = StackTop(&st);
StackPop(&st);
int div = PartSort(a, left, right);
if(left<div-1)
{
StackPush(&st, left);
StackPush(&st, div-1);
}
if(div+1<right)
{
StackPush(&st, div+1);
StackPush(&st, right);
}
}
StackDestroy(&st)
}
用队列实现非递归快排
void QuickSortNonR(int* a, int left, int right)
{
Queue qu;
QueueInsert(&qu);
QueuePush(&qu,left);
QueuePush(&qu,right);
while(QueueEmpyt(&qu)!=0)
{
int left=QueueFront(&qu);
QueuePop(&qu);
int right=QueueFront(&qu);
QueuePop(&qu);
int keyi=PartSort(a,left,right);
if(left<keyi-1)
{
QueuePush(&qu,left);
QueuePush(&qu,keyi-1);
}
if(keyi+1<right)
{
QueuePush(&qu,keyi+1);
QueuuPush(&qu,end);
}
}
QueueDestory(&qu);
}
6.堆排序
步骤一:向下调整法
void AdjustDown(int* a, size_t size, size_t root)
{
size_t parent=root;
//假设需要交换的是左孩子
size_t child=parent*2+1;
while(child<size)
{
//如果右孩子存在且比右孩子小
if(child+1<size&&a[child+1]<a[child])
{
child++;
}
if(a[child]>a[parent])
{
Swap(&a[child],&a[parent]);
parent=child;
child=parent*2+1;
}
else
{
break;
}
}
}
步骤二
void HeapSort(int*a,int n)
{
//先建堆,从最后一个元素的parent开始,最后一层的结点本来就是堆,所以不用进行排序
//建立大堆
for(int i=(n-1-1)/2;i>=0;i--)
{
//向下调整
AdjustDown(a,n,i);
}
size_t end=n-1;
while(end>0)
{
Swap(&a[0],&a[end]);
AdjustDown(a,end,0);
end--;
}
}
7.归并排序
递归归并排序
void _MergeSortNonR(int* a, int begin,int end,int*tmp)
{
if(begin>=end)
return ;
int mid=(begin+end)/2;
//如果不按照[begin,mid][mid+1,end]的方式划分,可能会出现死循环
_MergeSortNonR(a,begin,mid,tmp);
_MergeSortNonR(a,mid+1,end,tmp);
//对已经排好序的两个区间进行归并排序
int begin1=begin,end1=mid;
int begin2=mid+1,end2=end;
int index=begin;
while(begin1<=end1&&begin2<=end2)
{
if(a[begin1]<a[begin2])
tmp[index++]=a[begin1++];
else
tmp[index++]=a[begin2++];
}
while(begin1<=end1)
tmp[index++]=a[begin1++];
while(begin2<=end2)
tmp[index++]=a[begin2++];
memcpy(a+begin,tmp+begin,(end-begin+1)*sizeof(int));
}
void MergeSortNonR(int* a, int n)
{
int*tmp=(int*)malloc(sizeof(int)*n);
assert(tmp);
_MergeSortNonR(a,0,n-1,tmp);
free(tmp);
}
改成非递归
//利用gap控制步长
void _MergeSortNonR(int*a,int begin.int end,int*tmp)
{
int gap=1;
while(gap<n)
{
for(int i=0;i<n;i+=gap*2)
{
int begin1=i,end1=i+gap-1;
int begin2=i+gap,end2=i+gap*2-1;
int index=i;
while(begin1<=end1&&begin2<=end2)
{
if(a[begin1]<a[begin2])
tmp[index++]=a[begin1++];
else
tmp[index++]=a[begin2++];
}
while(begin1<=end1)
tmp[index++]=a[begin1++];
while(begin2<=end2)
tmp[index++]=a[begin2++];
memcpy(a+begin,tmp+begin,(end-begin+1)*sizeof(int));
gap=gap*2;
}
}
void MergeSortNonR(int* a, int n)
{
int*tmp=(int*)malloc(sizeof(int)*n);
assert(tmp);
_MergeSortNonR(a,0,n-1,tmp);
free(tmp);
}
如果只是把越界的边界改为n-1,有部分区间就会遍历多次,index++就会发生越界访问
对于这一组数来说,前面两组步长为4的组正常归并,得到的结果为[1,6,7,10],[2,3,4,9];如果只是把越界的部分修改为n-1。那么最后一组的归并元素的下标为[8,9],[9,9]。对区间[8,9]进行归并,得到的结果为[2,5]。此时的++index=10,而另一部分的区间被我们修正为了[9,9]。所以继续归并一个数5,++index=11,发生越界访问。
因此,对于三种不同的越界情况,需要进行不同的修正
- 对于[begin1,end1]由于end1,导致的越界访问,直接把end1修正为n-1;
- 对于[begin2,end2]由于begin2和end2都有越界的可能,所以分情况讨论
- 如果begin2没有越界,而end2越界了,把end2修改为n-1即可
- 如果begin2和end2都发生越界,就把该区间修改为一个不存在的区间
//利用gap控制步长
void _MergeSortNonR(int*a,int begin.int end,int*tmp)
{
int gap=1;
while(gap<n)
{
for(int i=0;i<n;i+=gap*2)
{
int begin1=i,end1=i+gap-1;
int begin2=i+gap,end2=i+gap*2-1;
int index=i;
while(begin1<=end1&&begin2<=end2)
{
if(a[begin1]<a[begin2])
tmp[index++]=a[begin1++];
else
tmp[index++]=a[begin2++];
}
//设置条件断点
//if(begin1==8 &&end1==9 &&begin2==9 &&end2==9)
//{
//打一个断点
//int x=0;
//}
if(end1>end)
{
end1=n-1;
}
//如果begin2大于了end,那么这个区间就一定不存在
if(begin2>end)
{
begin2=n;
end2=n-1
}
if(end2>end)
{
end2=n-1
}
while(begin1<=end1)
tmp[index++]=a[begin1++];
while(begin2<=end2)
tmp[index++]=a[begin2++];
memcpy(a+begin,tmp+begin,(end-begin+1)*sizeof(int));
gap=gap*2;
}
}
void MergeSortNonR(int* a, int n)
{
int*tmp=(int*)malloc(sizeof(int)*n);
assert(tmp);
_MergeSortNonR(a,0,n-1,tmp);
free(tmp);
}
8.计数排序
void CounSort(int*a,int n)
{
int max=a[0],min=a[0];
for(int i=0;i<n;i++)
{
if(a[i]>max)
max=a[i];
if(a[i]<min)
min=a[i];
}
//找到数据的范围
int range=max-min+1;
int*res=(int*)malloc(sizeof(int)*range);
memset(res,0,sizeof(int)*res);
for(int i=0;i<n;i++)
{
//计数器
res[a[i]-min]++;
}
int index=0;
for(int i=0;i<range;i++)
{
while(res[i]--)
{
a[index++]=i+min;
}
}
}
9.题目
题目1
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hkdR8iFH-1650528948534)(C:/Users/%E5%88%98%E9%91%AB/AppData/Roaming/Typora/typora-user-images/image-20220418232440060.png)]
int* shortestToChar(char * s, char c, int* returnSize)
{
int len=strlen(s);
int*res=(int*)malloc(sizeof(int)*len);
int prev=-len;
//左向右遍历,找字符与左C的最近距离
for(int i=0;i<len;i++)
{
if(s[i]==c)
{
prev=i;
}
res[i]=i-prev;
}
//右向左遍历,找字符与右C的最近距离
for(int i = prev-1;i>=0;i--)
{
if(s[i] == c)
{
prev = i;
}
if(res[i] > prev-i)
{
res[i] = prev-i;
}
}
*returnSize=len;
return res;
}
总结:排序的时间检验
void TestOP()
{
srand(time(0));
const int N = 1000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
//InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
//ShellSort(a2, N);
int end2 = clock();
int begin7 = clock();
//BubbleSort(a7, N);
int end7 = clock();
int begin3 = clock();
//SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
//HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort1(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
QuickSort2(a6, 0, N - 1);
int end6 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("BublleSort:%d\n", end7 - begin7);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort1:%d\n", end5 - begin5);
printf("QuickSort2:%d\n", end6 - begin6);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}