puzzle(15)拼图类问题
目录
一,数字拼图——滑动
1,链接
2,游戏规则
3,术语
4,总状态数奇偶不变定理
5,判定——必要性
6,极小化
7,策略(化为子问题)
8,判定——充分性
9,OJ实战
SGU 139 Help Needed
二,数字拼图——旋转
三,数字拼图——轮换
四,纯色块拼图——旋转
五,六边形纯色块拼图——旋转
六,纯色块拼图——轮换
七,色块拼图
一,数字拼图——滑动
1,链接
4399拼图游戏
或者我是最强大脑这个app中的数字华容道小游戏中的经典模式。
2,游戏规则
给你一个n(n>1)行m(m>1)列的矩阵,刚好由0,1,2。。。。。。n*m-1这n*m个数组成。
通过一系列的操作,使得矩阵变成如下状态(以下简称复原状态):
按照从上到下(一级排序),从左到右(二级排序)来排序,矩阵可以排成数列1,2,3,4。。。。。。n*m-2,n*m-1,0
操作只有1种,0和0的若干邻居(上下左右,最多4个邻居)中的某一个交换位置。
拼图游戏里面,0对应的格子是空的。
3,术语
逆序:
对于n个不同的元素,先规定个元素之间有一个“标准次序”(例如n个不同的自然数,可规定由小到大为标准次序),于是在这n个元素的任一排列中,当某两个元素的先后次序与标准次序不同时,就有1个“逆序”。点击打开百科词条
逆序数:
一个排列中所有逆序的总数叫做这个排列的“逆序数”。点击打开百科词条
曼哈顿距离:
固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。点击打开百科词条
总状态数:
逆序数是数列的一种状态数,曼哈顿距离是线段的一种状态数。
同样的,对于如上所说的n*m的矩阵,也可以定义总状态数。
总状态数=逆序数+0所在的格子到右下角的格子的曼哈顿距离(以下简称曼哈顿距离)。
4,总状态数奇偶不变定理
对于一个序列,每交换任意2个数,逆序数的奇偶性都会改变1次。
对于拼图游戏,每交换一次,曼哈顿距离的值都加1或者减1,所以奇偶性也会改变1次。
所以说,对于拼图游戏,总状态数的奇偶性是永远不变的。
5,判定——必要性
任何1个n*m的矩阵,是否都能移成复原状态呢?不一定。
首先,复原状态的总状态数的奇偶性可以算出来,曼哈顿距离为0,逆序数为n*m-1
所以总状态数的奇偶性就是n*m-1的奇偶性。
那么,对于任意给定的矩阵,很明显有的状态的奇偶性符合,有的却不符合。
根据总状态数奇偶不变定理,奇偶性不对的肯定无法复原,比如
这个状态的逆序数为15,曼哈顿距离为0,所以这个状态为奇,
而总状态数的奇偶性是3*5-1=14为偶,所以这个状态肯定无法复原。
有的状态是可以复原的,比如
这个状态的逆序数为14,曼哈顿距离为4,和为偶,经验证,这个状态是可以复原的。
说起来,这2个图就是上面的链接里面的4399游戏截图的,因为初始化比较慢,
而且还没初始化完就可以开始点了,于是我侥幸能得到这2张图。
那么,是不是只要状态的奇偶性对了,就一定可以复原呢?
这个值得思考,请继续看!
6,极小化
对于2*2的拼图,只有4!=24种状态。n=2,m=2,n*m-1=3
可以验证,有12种奇状态,全部可以复原,有12种偶状态,全部无法复原。
7,策略(化为子问题)
对于假设可以复原的状态,要怎么样复原呢?
第一,若 n>2,那么一定可以复原第一行,接下来只需要解决(n-1)*m 的子问题。
请注意,既然是子问题,那么第一行当然是永不再变,下同。
还请注意,因为加了这个限制,原问题有解不代表子问题同样有解。
第二,若m>2,那么一定可以复原第一列,接下来只需要解决 n*(m-1)的子问题。
第三,通过反复运用上述2条结论,最终一定可以只剩下右下角的4个格子,即2*2的子问题。
8,判定——充分性
如果一个状态的奇偶性和n*m-1的奇偶性相同,那么通过上述策略(七)化成2*2的子问题之后,
得到的状态的奇偶性和n*m-1的奇偶性仍然相同(四)。
根据(六),一定可以复原。
综上所述,当且仅当一个状态的奇偶性和n*m-1的奇偶性相同时,可以复原。
9,OJ实战
SGU 139 Help Needed
题目:
Description
Little Johnny likes puzzles a lot! Just a few days ago, he found out about the 'traditional' 4x4 puzzle. For this puzzle, you have all the numbers from 0 to 15 arranged in 4 rows and 4 columns. You are allowed to switch two adjacent elements (horizontally or vertically), only if one of them has the value 0. The purpose of the puzzle is to reach the following final state:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 0
Given the initial state of the puzzle, you have to decide whether there exists a sequence of moves which brings the puzzle into the final state.
Input
The input will consist of 4 lines, each of them containing 4 integers, describing the initial state of the puzzle.
Output
For every initial state, you should print "YES" if the final state can be reached after several moves or "NO", if such a thing is impossible.
Sample Input #1
1 2 3 4
5 6 7 8
9 10 11 0
13 14 15 12
Sample Output #1
YES
Sample Input #2
2 1 3 4
5 6 7 8
9 10 11 12
0 13 14 15
Sample Output #2
NO
这个题目是说,输入16个数,0-15,问你这样的状态能不能复原。
代码:
#include
using namespace std;
int list[16];
int main()
{
int sum = 0;
for (int i = 0; i < 16; i++)
{
cin >> list[i];
for (int j = 0; j < i; j++)if (list[j]>list[i])sum++;
if (list[i] == 0)sum += i / 4 + i % 4;
}
if (sum % 2)cout << "YES";
else cout << "NO";
return 0;
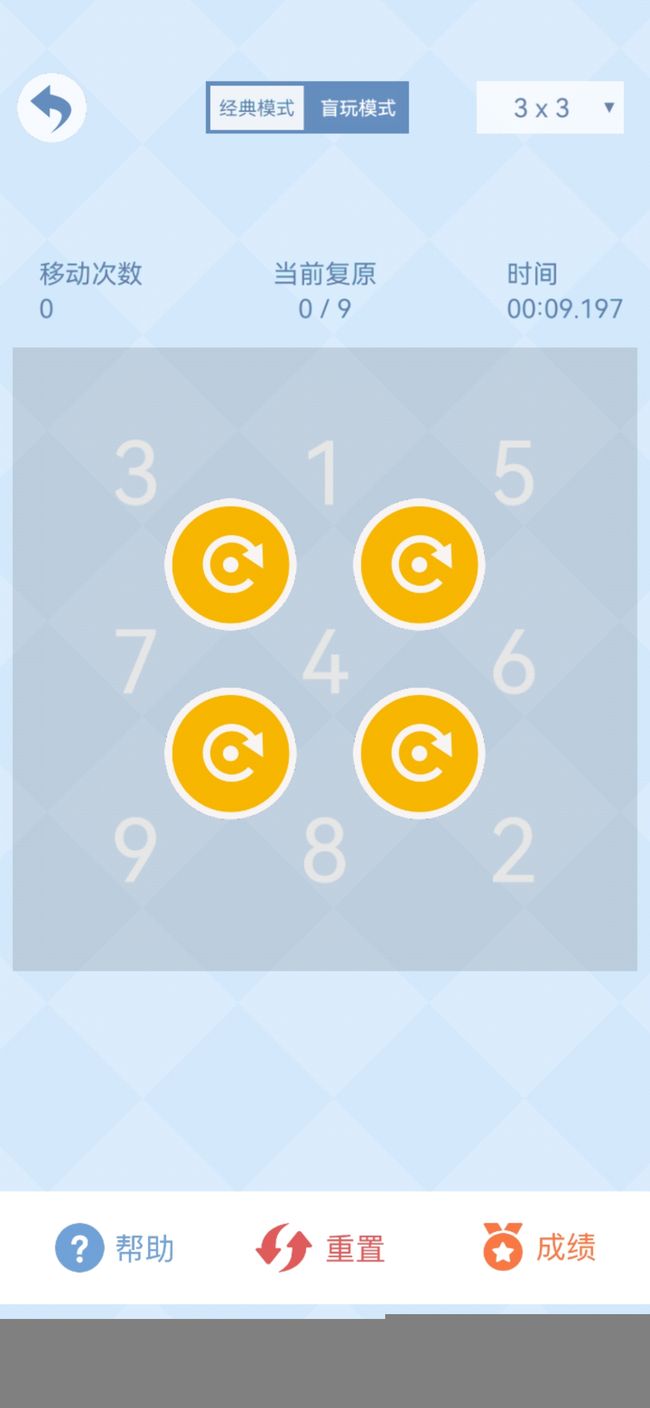
} 二,数字拼图——旋转
数字华容道小游戏中的旋转模式
很容易把第一行和第一列搞定,关键是右下角四个怎么排序。
出现这种情况,需要把5和6反过来。显然只要知道怎么交换5和6,就能轻松应付所有情况了。
经过几次尝试,我把公式找出来了,左上的旋转按钮是不需要的,所以我把其他三个按钮分别叫做上左右。
公式就是上上左上右上上右右左右右右左右右右,这17个操作下来,就把5和6对换了,其他的不动。
对于更高阶的情况,都可以直接化成3*3的情况,方法和数字拼图——滑动的方法一样。
三,数字拼图——轮换
数字华容道小游戏中的联动模式。
(1)3*3
先把前2行弄好,最后一行一定是OK的,只要左右滑动即可。
(2)4*4
对于4*4的情况,很容易把前2行搞定,然后把下面2行的左边3列搞定。
唯一需要思考的就是,如何把相邻的2个对换位置。
很明显,只要知道如何交换这2个,就能轻松应付所有情况了。
方法一:
方法就是只滑动第三行和第四列,左上左左下左上右下右上左下左左 即可。
这个公式是我大学发明的,过去了好几年,不记得咋搞出来的了,估计是试出来的。
我在尝试推广到5*5时遇到了障碍,所以我研究了这个公式的本质,发现可以化简。
方法二:
我们只滑动第二行和第四列,左上右下下左上右上 即可。
(3)5*5
对于5*5的情况,不会出现只有2个是反着的情况,所以不需要公式。
(4)6*6
如果对第一行和第六列,左上右下下左上右上,相当于把第六列的中间四个循环往上挪了一格。
所以公式是:
先对第四行第六列,左上右下下左上右,再对第二行第六列,左上右下下左上右上
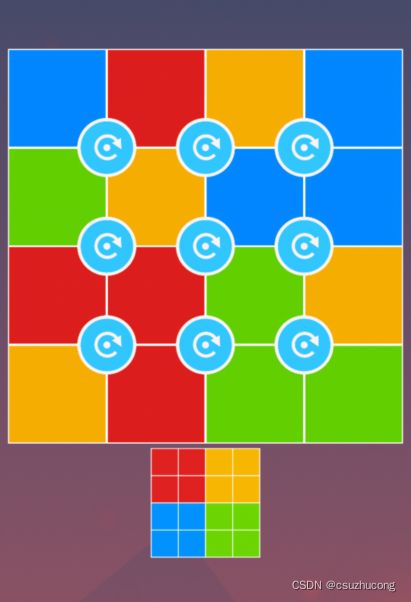
四,纯色块拼图——旋转
这种纯粹就是数字拼图——旋转的简化版。
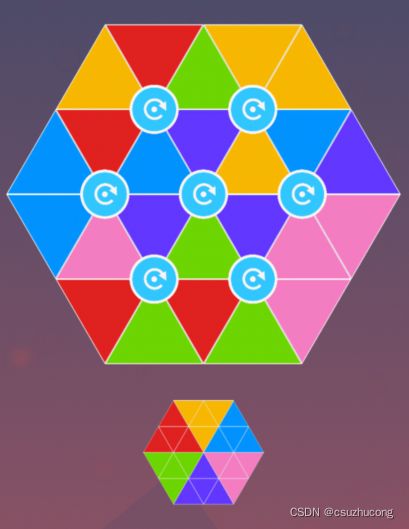
五,六边形纯色块拼图——旋转
各种数字旋转、色块旋转的puzzle都和魔方是类似的。
六,纯色块拼图——轮换
这种纯粹就是数字拼图——轮换的简化版。
方法也是一样的,对于3*3,先把第一行搞定,再把下面两行的左边两列搞定,最后把右下角2个块一交换即可。
对于5*5的,需要2次解决交换问题。
七,色块拼图
先把边界一圈的拼好,其他的按照横着的和竖着的分开。
再从边界逐渐往里面拼,主要关注大狗狗
搞定。