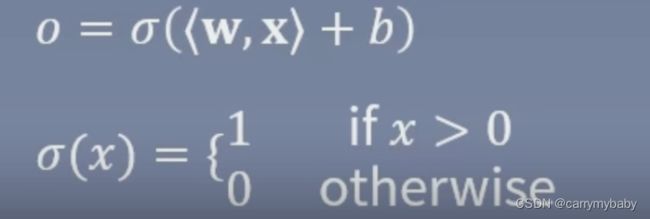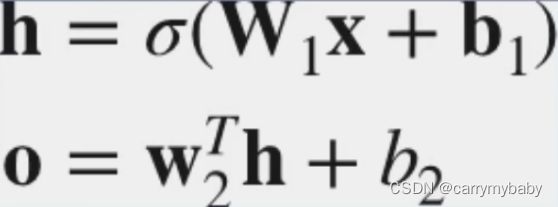神经网络浅学

分为以下三步走

神经网络与多层感知机：包括基础知识，激活函数、反向传播、损失函数、权值初始化和正则化

卷积神经网路：统治图像领域的圣经网络结构，发展历史、卷积操作和池化操作

循环神经网路：统治序列数据的神经网络结构，RNN、GRU、LSTM

有许多人不明白深度学习、机器学习、神经网络、人工智能这四者之间的关系，下面看这张图：

可以看到，这四者的包含关系，就不详细讲解。

开始正式的内容，第一部分：

1、人工神经元

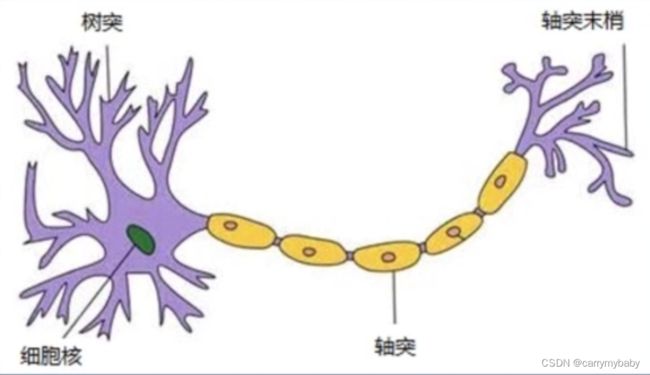
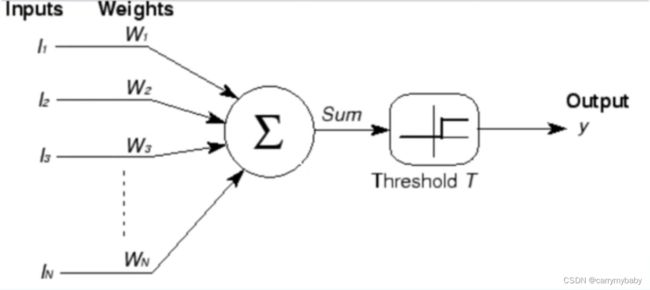
人工神经元是人类神经元中抽象出来的数学模型，人类的神经元中，树突负责接收别的神经元传递过来的信息，细胞核负责对信息进行一系列处理，轴突和轴突末梢用来传递处理好的信息。对应人工神经元的示意图如下（M-P模型）。

人工神经网络是大量神经元以某种连接方式构成的机器学习模型。

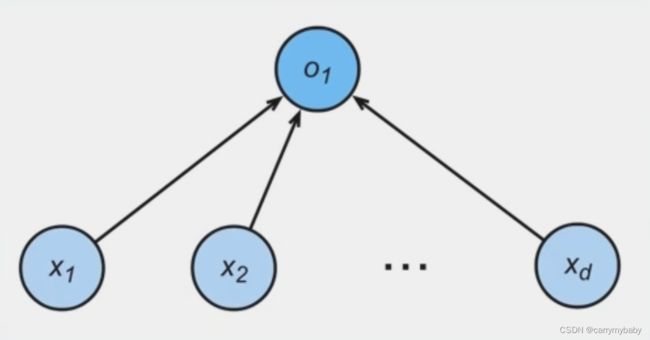
第一个神经网络：Perceptron（感知机）

 其中b为偏置项，在结构图中不会绘制出来。

 感知机的致命缺点：Perceptron无法解决异或问题（1969证明）。在二维平面内Perceptron就是一条直线，想象一下，异或问题的（0，0）（1，1）为0，（1，0）（0，1）为1，是无法用一条直线进行分类的。

2、多层感知机

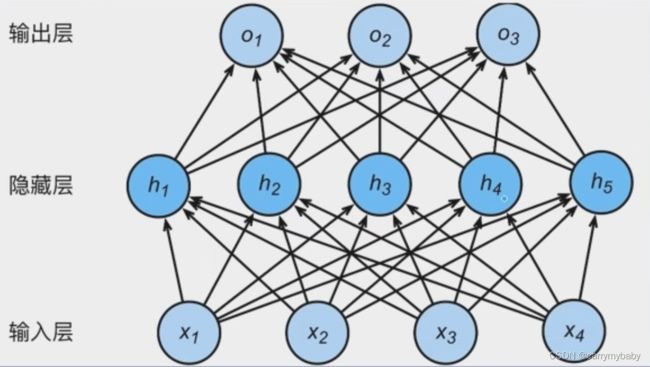
单层网络基础上引入一个或多个隐藏层，是神经网络有多个网络层，因而得名多层感知机。

上图为一个两层网络结构，因为只有两个网络层有权重参数。在多层感知机中权重参数一般写为矩阵的形式，上图中，第一层权重为四行五列的矩阵，因为输入有四个，输出有五个，隐藏层到输出层就是五行三列的权重矩阵。

 多层感知机的前向传播，数据是怎么从输入层到输出层的：

输入X，可以理解为一个1*4的向量，乘以一个4*5的权重矩阵（加上一个偏置），得到一个1*5的隐藏层向量H，H乘以一个5*3的权重矩阵（偏置）得到一个1*3的输出层O。

重点：在多层感知机中，隐藏层中必须加入激活函数，如果没有，网络就会退化为单层网络。原因是在矩阵运算过程中，矩阵乘法是可以相乘的，所以输出应该加上（如下图公式）一个sigema。

3、激活函数

作用：

（1）、让多层感知机成为真正的多层。

（2）、引入非线性，是网络可以逼近任意非线性函数（万能逼近定理，universal approximator）

激活函数需要具备的几个性质：

（1）、连续并可导（允许少数点不可导），便于利用数值优化的方法来学习网络参数。

（2）、激活函数及其导函数要尽可能地简单，有利于提高网络计算效率。

（3）、激活函数地导函数的值域要在合适的区间内，太大或太小都会影响训练的效率和稳定性。

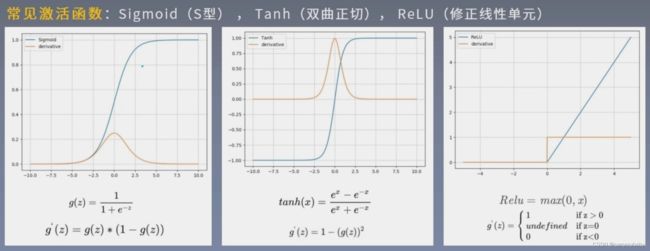
 sigmoid在RNN圣经网络中使用的比较多，函数值区间在0-1，正好是概率分布的区间范围，所以经常拿来做二分类的问题，在各种循环神经网络，也会拿来做门控单元的激活函数，用来控制信息的流动（是保留还是遗忘）。再看到导函数，导函数接近0的时候，函数的梯度也就接近0，称为饱和区，sigmoid函数的饱和区比较大（这也是弊端），如果神经元落入饱和区，就很难进行前向的传播。

tanh形状和sigmoid相似，但是值域是-1到1，上下对称，可以大致的认为均值为0，利于神经网络的训练。其导函数和S型差不多，也不利于前向传播。S和T中间的区域（导函数不为0的区域）一般认为是一个线性区域。

reli与前两个不同，他没有饱和区，在深度神经网络中经常使用。

激活函数有两大类，一类是以S,T为代表的饱和型激活函数，一类是以ReLu为代表的非饱和激活函数，非饱和激活函数一般在做好优化时会对负半轴进行优化。

4、反向传播

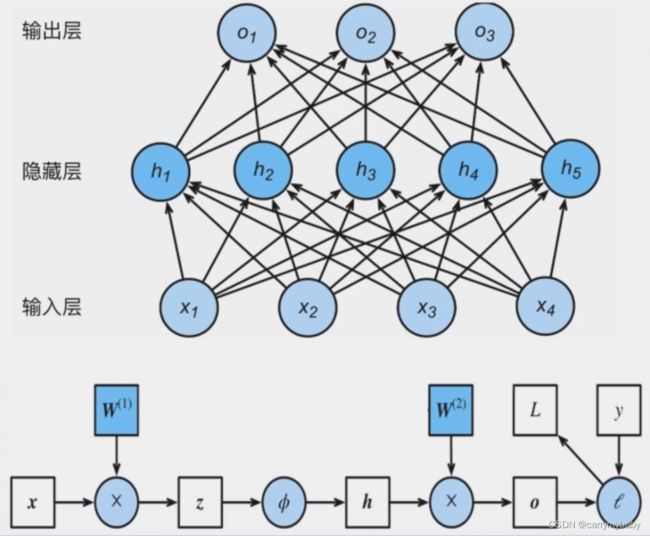
前向传播：输入层数据开始从前向后，逐步传递至输出层。

反向传播：损失函数开始从后向前，梯度逐步传递至第一层。

反向传播作用：永贵权重更新，时网络输出更接近标签。

损失函数：衡量模型输出与真实标签的差异（loss）越小越好。

反向传播原理：链式求导法则

 

示意图中，节点用举行表示，表示的是数据，边用圆圈来表示，表示操作。

 梯度下降法：权重沿着梯度负方向更新，使函数数值减小。

导数：函数在指定坐标轴上的变化率！！！注意是指定坐标轴！！

方向导数（在多元函数上的概念）：指定方向上的变化率。

梯度：一个向量，方向为方向导数取得最大值的方向。

学习率：控制更新步长。（现在一般学习率都是变化的，比如yolov5中使用的预热学习率,采用的余弦退火模型来对学习率进行更新）

5、损失函数

衡量模型输出与真实的标签之间的差距。

有三个比较容易混淆的概念，Loss Function、Cost Function、Objective Function，损失函数描述的是单样本损失函数，代价函数算的是总体损失的平均值，目标函数由两线构成，Obj=Cost+RegularizationTerm（正则项），正则项是为了控制模型的复杂程度，防止模型过拟合。一般在优化模型的时候，只考虑减小loss值，公式定义上讲的还是优化目标函数（写论文嘛）。介绍两种常用的损失函数计算公式：MSE、CE

信息熵描述的是信息的不确定度，值等于所有可能取值的信息量的期望（不太好理解，查一下百度吧）

相对熵：又称K-L散度，衡量两个分布之间的差异（公式可以去百度找一下）。

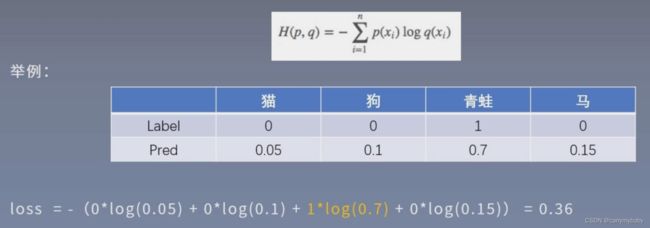
交叉熵=信息熵+相对熵

所以优化交叉熵等价于优化相对熵。

 计算交叉熵举例：

 在输出前，还会经过一个Softmax操作，使得输出的概率值和为1。

没有一个适合所有任务的损失函数，损失函数设计会涉及算法类型、求导是否容易、数据中异常值的分布等问题。感兴趣可以到（https://pytorch.org/docs/stable/nn.html#loss-functions）进一步学习。

6、权值初始化

训练前对权值参数赋值，良好的权值出啊实话有利于模型训练。

通常采用随机初始化方法：高斯分布随机初始化，从高斯分布中随机采样，对权重进行赋值。数值分布在（区间u+-3a）中的概率是99.73%，所以概率分布的标准差影响了权重的分布，而影响概率分布的参数就是标准差。标准差也有确定的方法。

自适应标准差：自适应方法随机分布中的标准差，下面是几种方法。

Xavier初始化

Kaiming初始化（MSRA）

7、正则化

Regularization：减小方差的策略，通俗理解为减轻过拟合的策略。

误差可以分解为：偏差、方差、噪声之和。

偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的你和能力。

方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。

噪声则表达了在当前任务上学习算法所能达到的期望泛化误差的下界。

常见的两种正则项：

L1：     L2：   下图更易理解

（花书的第七章，有关于正则项的详细的理论证明）

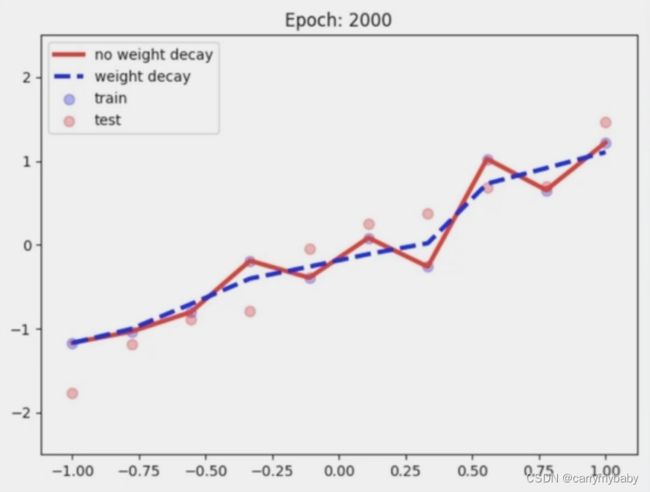
上图中彩色的一圈一圈的线是cost的等高线，没有加入正则项的时候，一个圈中的所有点都是相等的，加入正则项时，就需要找到一个圆里面正则项最小的点，就是相切的点。

在神经网络的优化过程中，会经常看到一个词叫做weight decay(权值衰减)，就是在目标函数中加入了L2正则项，具体推导过程看花书。

 

常见的正则化方法：

 Dropout：随机失活（字面意思，随机把神经元的权重将为0，但不会将神经元删除，每次都随机失火几个神经元，这样做会大大提高网络的多样性，避免过拟合）

优点：避免过度依赖某个神经元，实现减轻过拟合

注意事项：训练和测试两个阶段的数据尺度变化

 怎么理解尺度变化：训练阶段会有神经元的失活，测试阶段就会将神经元全部启用，所以，测试时，神经元输出值需要乘以p（随机失活的概率）。

还有其他许多高级的正则化的方法，比如Batch normalization（现在神经网络的标配）等，自行查阅资料。