融合黄金正弦和曲线自适应的多策略麻雀搜索算法
文章目录
- 一、理论基础
-
- 1、原始麻雀搜索算法(SSA)
- 2、融合黄金正弦和曲线自适应的多策略麻雀搜索算法(GCSSA)
-
- 2.1 Chebyshev混沌映射策略
- 2.2 位置更新方式改进
-
- 2.2.1 黄金正弦策略(Golden sine strategy)
- 2.2.2 曲线自适应策略(Curve adaptive strategy)
- 2.3 最优位置扰动策略
-
- 2.3.1 随机游走扰动策略
- 2.3.2 柯西-t扰动策略
- 2.4 算法实现流程
- 二、仿真实验结果与分析
- 三、参考文献
一、理论基础
1、原始麻雀搜索算法(SSA)
请参考这里。
2、融合黄金正弦和曲线自适应的多策略麻雀搜索算法(GCSSA)
本文针对SSA全局搜索性较差、早熟收敛、陷入局部最优等不足,提出一种融合黄金正弦和曲线自适应的多策略麻雀搜索算法(GCSSA),具体改进策略如下。
2.1 Chebyshev混沌映射策略
本文采用Chebyshev混沌映射来初始化种群,相比于Tent混沌映射对混沌系统初始状态和系统参数异常敏感,Chebyshev映射数学表达式简单,没有系统参数,初值敏感性相对不高,鲁棒性强。Tent和Chebyshev混沌映射表达式分别如式(1)和式(2)所示。 x t + 1 = { x t a , x t < a 1 − x t 1 − a , x t ≥ a (1) x_{t+1}=\begin{dcases}\frac{x_t}a,\quad\quad\,\,\,\, x_t


2.2 位置更新方式改进
位置更新方式是决定一个模型好坏最重要的环节。本节针对SSA中发现者和加入者位置更新方式作出改进来提高算法性能。
2.2.1 黄金正弦策略(Golden sine strategy)
黄金正弦算法(Golden sine algorithm, Golden-SA)的数学模型请参考这里。
对于麻雀搜索算法,迭代过程中发现者们占据当前适应度值较高的位置,从而领导整个种群进行觅食,但是这些发现者之间缺乏足够的交流,黄金正弦可以很好的弥补这一不足。引入黄金正弦后的发现者更新位置方式: X i , j t + 1 = { X i , j t ⋅ ∣ sin ( r 1 ) ∣ − r 2 ⋅ sin ( r 1 ) ⋅ ∣ c 1 X P t − c 2 X i , j t ∣ R 2 < S T X i , j t + Q ⋅ L R 2 ≥ S T (3) X_{i,j}^{t+1}=\begin{dcases}X_{i,j}^t\cdot|\sin(r_1)|-r_2\cdot\sin(r_1)\cdot|c_1X_P^t-c_2X_{i,j}^t|\quad R_2
2.2.2 曲线自适应策略(Curve adaptive strategy)
受改进粒子群算法中惯性权重思想的启发,为了更好的协调全局搜索和局部挖掘能力,改善算法在迭代的中后期快速收敛落入局部最优的问题。在黄金正弦更新公式中引入曲线自适应权重 w 1 w_1 w1,表达式如下: w 1 = ( c o s ( π ⋅ t / T max ) + w max ) ( w max + w min ) / 2 + a (4) w_1=(cos(\pi\cdot t/T_{\max})+w_{\max})(w_{\max}+w_{\min})/2+a\tag{4} w1=(cos(π⋅t/Tmax)+wmax)(wmax+wmin)/2+a(4)其中, t t t当前迭代次数, T max T_{\max} Tmax是最大迭代次数, a a a是调整系数, w max w_{\max} wmax是因子最大值, w min w_{\min} wmin是因子最小值。 w 1 w_1 w1在迭代前期保持缓慢下降,中期下降速度加快,后期再次减缓下降速度。既保证了前期能够减缓全局搜索性下降的同时,又改善了后期落入局部最优的问题。加入曲线自适应权重改进后的发现者位置更新公式如下: X i , j t + 1 = { ( 1 − w 1 ) ⋅ X i , j t ⋅ ∣ sin ( r 1 ) ∣ − w 1 ⋅ r 2 ⋅ sin ( r 1 ) ⋅ ∣ c 1 X P t − c 2 X i , j t ∣ R 2 < S T X i , j t + Q ⋅ L R 2 ≥ S T (5) X_{i,j}^{t+1}=\begin{dcases}(1-w_1)\cdot X_{i,j}^t\cdot|\sin(r_1)|-w_1\cdot r_2\cdot\sin(r_1)\cdot|c_1X_P^t-c_2X_{i,j}^t|\quad R_2
加入者的更新方式是以占据最优位置的发现者为目标而进行位置更新,SSA中加入者和发现者通过动态转换维持固定比例不变。为使加入者更好更快的跟随发现者进行位置更新,在改进的加入者更新方式中引入曲线自适应权重 w 2 = 1 − w 1 w_2=1-w_1 w2=1−w1, w 2 w_2 w2随迭代动态增加,使加入者后期能够以较大步长移动,防止因盲目跟随发现者而错过更好位置,进而改善算法过快收敛,陷入局部最优的问题。 w 2 w_2 w2的表达式以及改进后的加入者更新方式如下: w 2 = 1 − ( ( c o s ( π ⋅ t / T max ) + w max ) ( w max + w min ) / 2 + a ) (6) w_2=1-((cos(\pi\cdot t/T_{\max})+w_{\max})(w_{\max}+w_{\min})/2+a)\tag{6} w2=1−((cos(π⋅t/Tmax)+wmax)(wmax+wmin)/2+a)(6) X i , j t + 1 = { X i , j t ⋅ exp ( X w o r s t − X i , j t i 2 ) i > N / 2 X P t + 1 + w 2 ⋅ X P t + 1 O t h e r (7) X_{i,j}^{t+1}=\begin{dcases}X_{i,j}^t\cdot\exp\left(\frac{X_{worst}-X_{i,j}^t}{i^2}\right)\quad i>N/2\\X_P^{t+1}+w_2\cdot X_P^{t+1}\quad\quad\quad\quad\quad\, Other\end{dcases}\tag{7} Xi,jt+1=⎩⎨⎧Xi,jt⋅exp(i2Xworst−Xi,jt)i>N/2XPt+1+w2⋅XPt+1Other(7)经过多次实验,当 w max = 0.9 , w min = 0.2 , a = 0.45 w_{\max}=0.9,w_{\min}=0.2,a=0.45 wmax=0.9,wmin=0.2,a=0.45时,寻优结果最好。图2给出 w 1 w_1 w1迭代变化曲线图。

2.3 最优位置扰动策略
在SSA的后期迭代中,麻雀逐渐接近最优个体,引起种群多样性下降,陷入局部最优。为改善这一问题,本文通过动态选择两种扰动算子对搜索排序后的最优麻雀个体进行扰动,从而提高算法跳出局部最优的可能性。
2.3.1 随机游走扰动策略
参考蚁狮优化算法在蚁狮捕食蚂蚁时,蚂蚁通过随机游走的方式寻找食物更新其位置,蚂蚁随机游走公式如下: X ( t ) = [ 0 , c u m s u m ( 2 r ( t 1 ) − 1 ) , ⋯ , c u m s u m ( 2 r ( t n ) − 1 ) ] (8) X(t)=[0,cumsum(2r(t_1)-1),\cdots,cumsum(2r(t_n)-1)]\tag{8} X(t)=[0,cumsum(2r(t1)−1),⋯,cumsum(2r(tn)−1)](8)其中, X ( t ) X(t) X(t)为随机游走步数集合, c u m s u m cumsum cumsum为游走步数累加和, n n n是最大迭代次数, t t t表示随机游走的步数(本文中的迭代次数), r ( t ) r(t) r(t)是一个随机函数,定义如下: r ( t ) = { 1 i f r a n d > 0.5 0 i f r a n d ≥ 0.5 (9) r(t)=\begin{dcases}1\quad if\,\,rand>0.5\\0\quad if\,\, rand≥0.5\end{dcases}\tag{9} r(t)={1ifrand>0.50ifrand≥0.5(9)随机游走是基于式(8),蚂蚁在所有维度都用随机行走来更新他们的位置,每个维度的最优麻雀位置对应蚂蚁位置。由于搜索空间对可行域存在边界,不能直接用式(8)更新蚂蚁的位置。为确保蚂蚁在可行域范围内随机游走,根据式(10)对其进行归一化处理,处理后的 X b e s t t X_{best}^t Xbestt即最优麻雀随机游走扰动后的位置。 X b e s t t = ( X b e s t t − a i ) ⋅ ( d i t − c i t ) b i − a i + c i t (10) X_{best}^t=\frac{(X_{best}^t-a_i)\cdot(d_i^t-c_i^t)}{b_i-a_i}+c_i^t\tag{10} Xbestt=bi−ai(Xbestt−ai)⋅(dit−cit)+cit(10)式(16)中, a i a_i ai和 b i b_i bi分别为第 i i i维变量随机游走的最小值和最大值, c i t c_i^t cit和 d i t d_i^t dit分别为第 i i i个变量第 t t t次迭代的最小值和最大值。在开始迭代之初,随机游走边界较大,有利于提高全局搜索性,在迭代多次后,游走边界变小,从而提高算法的最优位置局部搜索性。
2.3.2 柯西-t扰动策略
引入柯西-t扰动算子的最优位置更新式如下: X b e s t t = X b e s t t [ 1 + λ 1 C a u c h y ( 0 , 1 ) ] + λ 2 t ( T max ) (11) X_{best}^{t}=X_{best}^t[1+\lambda_1Cauchy(0,1)]+\lambda_2t(T_{\max})\tag{11} Xbestt=Xbestt[1+λ1Cauchy(0,1)]+λ2t(Tmax)(11)其中, C a u c h y ( 0 , 1 ) Cauchy(0,1) Cauchy(0,1)是服从标准柯西分布的随机数, t ( T max ) t(T_{\max}) t(Tmax)是以最大迭代次数作为自由度的t分布随机数。柯西分布算子本身具有很好的扰动能力,可以提高全局搜索能力。t分布算子在自由度较低时类似柯西分布,扰动能力强,在自由度很高时类似高斯分布,可以增强局部挖掘能力。
通过 λ 1 \lambda_1 λ1、 λ 2 \lambda_2 λ2将两者相结合, λ 1 = 1 − t 2 / T max 2 , λ 2 = t 2 / T max 2 \lambda_1=1-t^2/T_{\max}^2,\lambda_2=t^2/T_{\max}^2 λ1=1−t2/Tmax2,λ2=t2/Tmax2是随迭代次数变化的自适应动态参数。在式(11)中, λ 1 \lambda_1 λ1初期值较大,因此柯西扰动占比较大,这有利于在较大范围对最优麻雀位置进行扰动,增强全局搜索性。 λ 2 \lambda_2 λ2后期值较大,此时t扰动占比较大,这有利于在最优麻雀位置附近探索,增强局部挖掘性,提高收敛精度。
根据动态选择概率来决定采取何种扰动策略,在一定概率下两种扰动策略交替执行,进一步增加最优位置扰动的随机性,提高跳出局部最优的可能性,表达式如下: P s = exp ( − ( 1 − t T max ) 20 ) + 0.05 (12) P_s=\exp\left(-\left(1-\frac{t}{T_{\max}}\right)^{20}\right)+0.05\tag{12} Ps=exp(−(1−Tmaxt)20)+0.05(12)具体选择策略的过程可以分成两种:第一种,当 r a n d < P s rand
2.4 算法实现流程
GCSSA算法具体实现流程如下:
步骤1 初始化参数,种群数量 N N N、最大迭代次数 T max T_{\max} Tmax、发现者比例( P D PD PD)、警戒者比例( S D SD SD)、曲线自适应权重最小值 w min w_{\min} wmin和最大值 w max w_{\max} wmax等。
步骤2 利用式(2)初始化麻雀种群,计算每只麻雀的适应度值并排序,找到当前最优适应度值和最差适应度值,以及所对应的麻雀位置。
步骤3 根据发现者比例,选取适应度值排名靠前的麻雀作为发现者,按照式(5)进行位置更新。
步骤4 剩余麻雀作为加入者,按照式(7)更新位置。
步骤5 从麻雀中种按照警戒者比例,随机选择警戒者,按照原始算法对应公式更新位置。
步骤6 计算更新每只麻雀的适应度值并排序,判断扰动条件。根据动态选择概率 P s P_s Ps(式12),选择随机游走扰动(式(8)-(10)或柯西-t扰动(式(11))对最优麻雀位置扰动。
步骤7 比较扰动后新的适应度值和原值,若新适应度值小于原值,则更新最优麻雀位置,反之,则保留原值。
步骤8 判断当前是否到达最大迭代次数,若是,结束循环输出最优结果,否则跳转步骤3。
二、仿真实验结果与分析
为公平比较不同元启发式算法的寻优性能,检测GCSSA改进策略的有效性,选取比较流行的4种基本元启发式算法与GCSSA进行对比实验,分别是麻雀搜索算法(SSA)、灰狼优化算法(GWO)、鲸鱼优化算法(WOA)、哈里斯鹰算法(HHO),所有算法种群数量设定为30,最大迭代次数为500,各算法独立运行30次。以文献[1]中表1的F1、F2、F3(30维/单峰函数)、F9、F10、F13(30维/多峰函数)为例,结果显示如下:
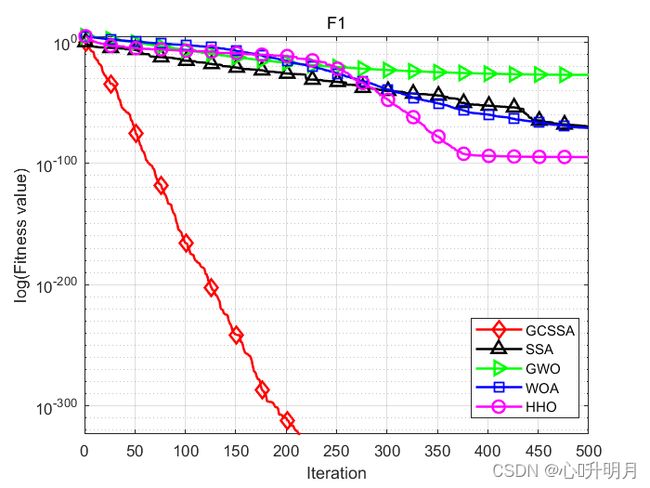
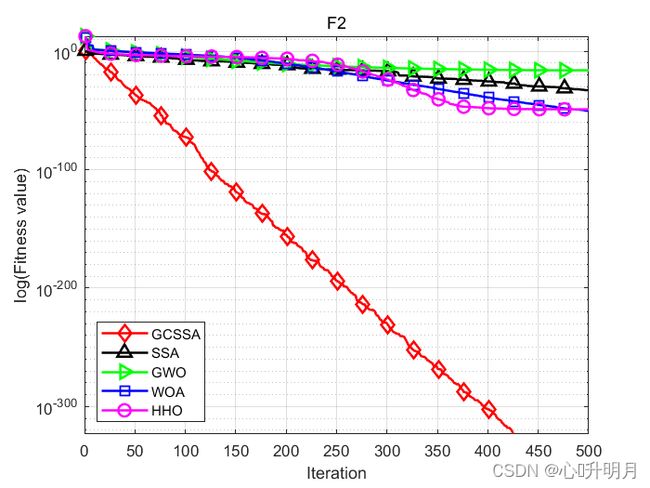
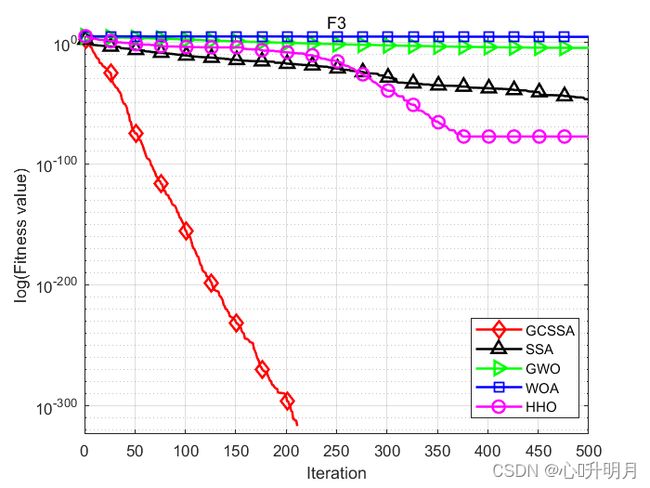


函数:F1
GCSSA:最差值: 0, 最优值: 0,平均值: 0,标准差: 0, 秩和检验: NaN
SSA:最差值: 4.2389e-69, 最优值: 0, 平均值: 1.413e-70, 标准差: 7.7391e-70, 秩和检验: 1.6572e-11
GWO:最差值: 6.7645e-27, 最优值: 1.7459e-29, 平均值: 9.9222e-28, 标准差: 1.4801e-27, 秩和检验: 1.2118e-12
WOA:最差值: 2.0849e-70, 最优值: 9.016e-86, 平均值: 6.9501e-72, 标准差: 3.8065e-71, 秩和检验: 1.2118e-12
HHO:最差值: 4.7499e-94, 最优值: 3.3682e-115, 平均值: 1.5893e-95, 标准差: 8.6709e-95, 秩和检验: 1.2118e-12
函数:F2
GCSSA:最差值: 0, 最优值: 0,平均值: 0,标准差: 0, 秩和检验: NaN
SSA:最差值: 4.5398e-32, 最优值: 1.6879e-138, 平均值: 1.5133e-33, 标准差: 8.2885e-33, 秩和检验: 1.2118e-12
GWO:最差值: 2.8678e-16, 最优值: 3.91e-18, 平均值: 8.8053e-17, 标准差: 6.7495e-17, 秩和检验: 1.2118e-12
WOA:最差值: 1.3544e-49, 最优值: 2.408e-57, 平均值: 7.0015e-51, 标准差: 2.5881e-50, 秩和检验: 1.2118e-12
HHO:最差值: 3.2066e-48, 最优值: 5.6349e-59, 平均值: 1.0841e-49, 标准差: 5.8518e-49, 秩和检验: 1.2118e-12
函数:F3
GCSSA:最差值: 0, 最优值: 0,平均值: 0,标准差: 0, 秩和检验: NaN
SSA:最差值: 3.7352e-46, 最优值: 1.599e-310, 平均值: 1.2978e-47, 标准差: 6.8156e-47, 秩和检验: 1.2118e-12
GWO:最差值: 0.00061762, 最优值: 4.0593e-08, 平均值: 3.533e-05, 标准差: 0.00012139, 秩和检验: 1.2118e-12
WOA:最差值: 71677.2438, 最优值: 26264.307, 平均值: 49464.1561, 标准差: 12815.0697, 秩和检验: 1.2118e-12
HHO:最差值: 6.8337e-77, 最优值: 2.7697e-108, 平均值: 2.3034e-78, 标准差: 1.2472e-77, 秩和检验: 1.2118e-12
函数:F9
GCSSA:最差值: 0, 最优值: 0,平均值: 0,标准差: 0, 秩和检验: NaN
SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO:最差值: 10.2624, 最优值: 0, 平均值: 1.7411, 标准差: 2.7489, 秩和检验: 1.6373e-11
WOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
HHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F10
GCSSA:最差值: 0, 最优值: 0,平均值: 0,标准差: 0, 秩和检验: NaN
SSA:最差值: 7.5441e-07, 最优值: 1.3331e-231, 平均值: 2.5147e-08, 标准差: 1.3774e-07, 秩和检验: 1.2118e-12
GWO:最差值: 0.0018865, 最优值: 1.8538e-17, 平均值: 0.0005212, 标准差: 0.00049652, 秩和检验: 1.2118e-12
WOA:最差值: 1.2921e-40, 最优值: 1.5195e-57, 平均值: 4.3073e-42, 标准差: 2.3591e-41, 秩和检验: 1.2118e-12
HHO:最差值: 2.4954e-05, 最优值: 3.3678e-58, 平均值: 8.3179e-07, 标准差: 4.5559e-06, 秩和检验: 1.2118e-12
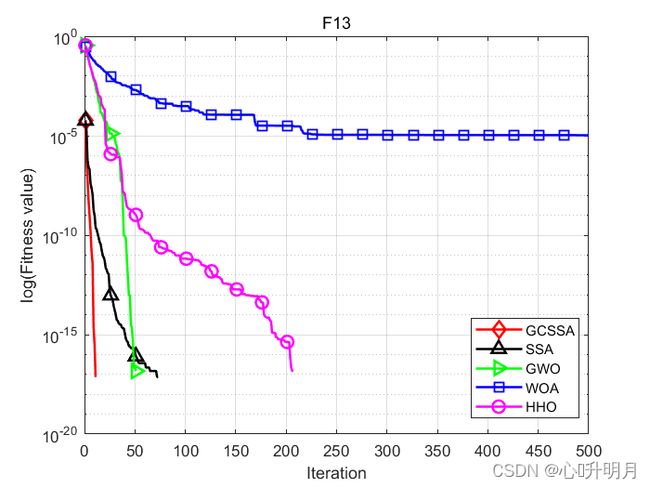
函数:F13
GCSSA:最差值: 0, 最优值: 0,平均值: 0,标准差: 0, 秩和检验: NaN
SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
WOA:最差值: 0.00031643, 最优值: 0, 平均值: 1.0548e-05, 标准差: 5.7772e-05, 秩和检验: 0.1608
HHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
结果表明,该改进算法在全局搜索性、克服局部最优、收敛速度、收敛精度、稳定性都有较大提升。
三、参考文献
[1] 高晨峰, 陈家清, 石默涵. 融合黄金正弦和曲线自适应的多策略麻雀搜索算法[J]. 计算机应用研究, 2022, 39(2): 491-499.