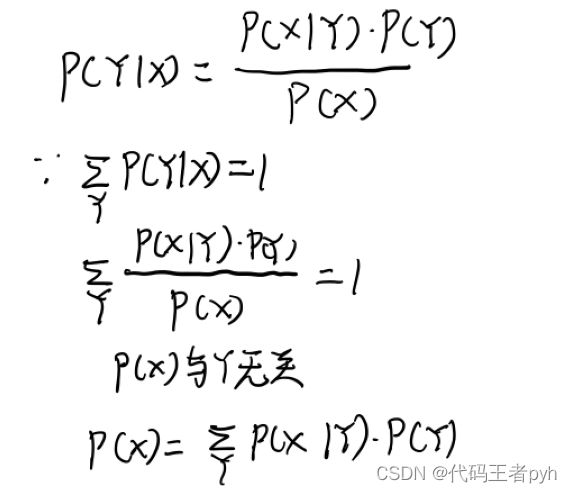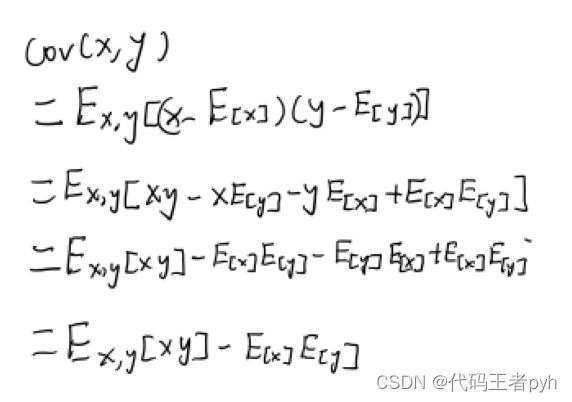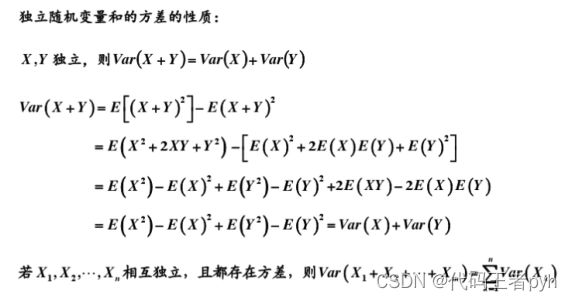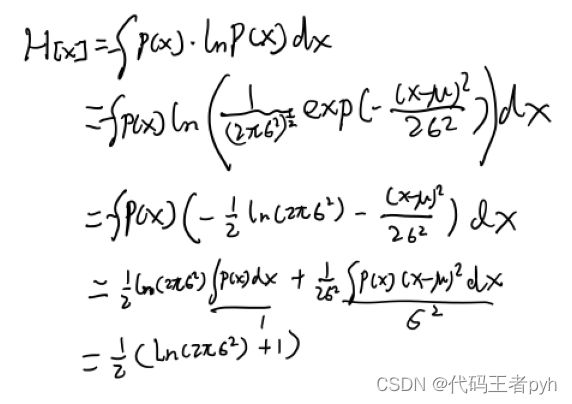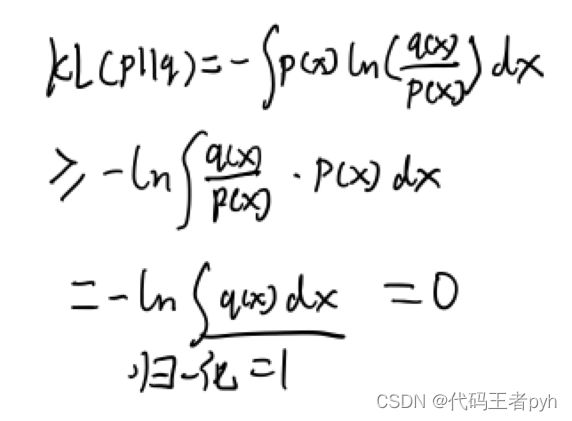PRML 模式识别与机器学习 1.绪论

1. 绪论

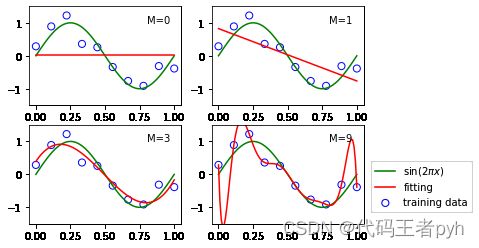
1.1. Example: Polynomial Curve Fitting

# sample data
def create_toy_data(func, sample_size, std):
    x = np.linspace(0, 1, sample_size)
    t = func(x) + np.random.normal(scale=std, size=x.shape)
    return x, t

def func(x):
    return np.sin(2 * np.pi * x)

x_train, y_train = create_toy_data(func, 10, 0.25)
x_test = np.linspace(0, 1, 100)
y_test = func(x_test)

plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.legend()
plt.show()

多项式拟合：

$$y(x,w)=w_0+w_{1}x+w_2{x}^2+...+w_M{x}^M=\sum _{j=0}^M{w}_j{x}^j\text{\hspace{1em}(1.1)}$$

误差函数

$$E(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N{\left\{y\left(x_n,\mathbf{w}\right)-t_n\right\}}^2\text{\hspace{1em}(1.2)}$$

目标是让误差函数越来越小。有唯一解$w^{\ast }$,是的$E(w)$取得最小值$E(w^{\ast })$。

# 几个多项式拟合
for i, degree in enumerate([0, 1, 3, 9]):
    plt.subplot(2, 2, i + 1)
    feature = PolynomialFeature(degree)
    X_train = feature.transform(x_train)
    X_test = feature.transform(x_test)

    model = LinearRegression()
    model.fit(X_train, y_train)
    y = model.predict(X_test)

    plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
    plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
    plt.plot(x_test, y, c="r", label="fitting")
    plt.ylim(-1.5, 1.5)
    plt.annotate("M={}".format(degree), xy=(0.8, 1))
plt.legend(bbox_to_anchor=(1.05, 0.64), loc=0, borderaxespad=0.)
plt.show()

m太大发生过拟合，泛化性能下降。需要一个衡量模型泛化能力的标准。

为了比较不同大小的数据集和保证和t有相同单位。引入均方根误差：

$$E_{RMS}=\sqrt{2E\left({\mathbf{w}}^{\ast }\right)/N}\text{\hspace{1em}(1.3)}$$

# 均方根对比
def rmse(a, b):
    return np.sqrt(np.mean(np.square(a - b)))

training_errors = []
test_errors = []

for i in range(10):
    feature = PolynomialFeature(i)
    X_train = feature.transform(x_train)
    X_test = feature.transform(x_test)

    model = LinearRegression()
    model.fit(X_train, y_train)
    y = model.predict(X_test)
    training_errors.append(rmse(model.predict(X_train), y_train))
    test_errors.append(rmse(model.predict(X_test), y_test + np.random.normal(scale=0.25, size=len(y_test))))

plt.plot(training_errors, 'o-', mfc="none", mec="b", ms=10, c="b", label="Training")
plt.plot(test_errors, 'o-', mfc="none", mec="r", ms=10, c="r", label="Test")
plt.legend()
plt.xlabel("degree")
plt.ylabel("RMSE")
plt.show()

解决过拟合的方式：

1. 增加样本个数

2. 正则化
   $$\tilde{E}(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N{\left\{y\left(x_n,\mathbf{w}\right)-t_n\right\}}^2+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2\text{\hspace{1em}(1.4)}$$
   $\Vert \mathbf{w}{\Vert }^2\equiv ={\mathbf{w}}_0^2+{\mathbf{w}}_1^2+...+{\mathbf{w}}_M^2$，$\lambda$的大小控制的正则化影响的大小

# M=9但用了正则化
feature = PolynomialFeature(9)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)

model = RidgeRegression(alpha=1e-3)
model.fit(X_train, y_train)
y = model.predict(X_test)

y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.annotate("M=9", xy=(-0.15, 1))
plt.show()

1.2 概率论

这里有两个随机变量，X和Y.（离散变量，相互独立）图中简化为{$x_1,x_2,x_3,x_4,x_5$}和{$y_1,y_2,y_3$}。N次取样，每次得到一组的x,y。$X=x_i,Y=y_i$的取到次数是$n_{ij}$。于是我们有

$$p\left(X=x_i,Y=y_i\right)=\frac{n_{ij}}{N}\text{\hspace{1em}(1.5)}$$

$$p\left(X=x_i\right)=\frac{c_i}{N}\text{\hspace{1em}(1.6)}$$

我们可以得到：

$$p\left(X=x_i\right)=\sum _{j=1}^{L}p\left(X=x_i,Y=y_i\right)\text{\hspace{1em}(1.7)}$$
这就是加法规则。$p\left(X=x_i\right)$被叫做边缘概率：因为它通过把其他变量(本例中的Y )边缘化或者加和得到。

条件概率：

$$p\left(Y=y_j|X=x_i\right)=\frac{n_{ij}}{c_i}\text{\hspace{1em}(1.8)}$$

$$p\left(X=x_i,Y=y_j\right)=\frac{n_{ij}}{N}=\frac{n_{ij}}{c_i}\cdot \frac{c_i}{N}=p\left(Y=y_j|X=x_i\right)p\left(X=x_i\right)\text{\hspace{1em}(1.9)}$$
这就是乘积规则。

sum rule $$p(X)=\sum _{Y}p(X,Y)\text{\hspace{1em}(1.10)}$$

product rule $$p(X,Y)=P(Y|X)p(X)\text{\hspace{1em}(1.11)}$$

根据这两个式子得到本书最重要的定义：贝叶斯定理。

$$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)}\text{\hspace{1em}(1.12)}$$

分子中的$P(x)={\sum }_{Y}P\left(X|Y\right)P\left(Y\right)$其实这就是加法规则。也确保了概率在归一化之后的值为1.

积分就是连续情况下的相加

1.2.1 概率密度

如果一个实值变量$x$落在区间$(x,x+\delta x)$的概率由$p(x)\delta x$给出，其中$ \delta x \to 0 $，那么我们就把$ p(x) $称作$ x $的概率密度（probability density）。

连续概率分布：

$$p(x\in (a,b))={\int }_a^{b}p(x)\mathrm{d}x\text{\hspace{1em}(1.24)}$$

满足：

$$p(x)\ge 0\text{\hspace{1em}(1.25)}$$

$${\int }_{-\infty }^{\infty }p(x)\mathrm{d}x=1\text{\hspace{1em}(1.26)}$$

可以用过Jacobian因子变化：例如:$x=g(y)$

$$p_y(y)=p_x(x)\left|\frac{\mathrm{d}x}{\mathrm{d}y}\right|=p_x(g(y))\left|g^{\prime }(y)\right|\text{\hspace{1em}(1.27)}$$

概率密度最大值的概念取决于变量的选择

定义累计密度分布：

$$P(z)={\int }_{-\infty }^{z}p(x)dx\text{\hspace{1em}(1.28)}$$

满足$$P^{\prime }(x)=p(x)$$
多变量的时候x是向量，定义是相似的。

加法法则和乘法法则

$$p(x)=\int p(x,y)dy\text{\hspace{1em}(1.31)}$$

$$p(x,y)=p(y|x)p(x)\text{\hspace{1em}(1.32)}$$

1.2.2 期望和方差

期望就是分布的平均

离散函数的期望：

$$\mathbb{E}[f]=\sum _{x}p(x)f(x)\text{\hspace{1em}(1.33)}$$
连续函数的期望:

$$\mathbb{E}[f]=\int p(x)f(x)dx\text{\hspace{1em}(1.34)}$$
当期望不好直接计算的时候：

$$\mathbb{E}[f]\simeq \frac{1}{N}\sum _{n=1}^{N}f(x_n)\text{\hspace{1em}(1.35)}$$
通过采样的方式来估计。

多变量情况下的期望,下标表示对谁求期望

$${\mathbb{E}}_x[f(x,y)]\text{\hspace{1em}(1.36)}$$
这是一个关于y的函数。

对于一个条件分布，同样有条件期望

$$\mathbb{E}[f|y]＝\sum _{x}p(x|y)f(x)\text{\hspace{1em}(1.37)}$$

方差就是分布在均值附近的变化性大小

定义为：

$$var[f]=\mathbb{E}[(f(x)-\mathbb{E}[f(x)]{)}^2]\text{\hspace{1em}(1.38)}$$
也可以写成

$$var[f]=\mathbb{E}[f(x{)}^2]-\mathbb{E}[f(x){]}^2\text{\hspace{1em}(1.39)}$$
所以

$$var[x]=\mathbb{E}[x^2]-\mathbb{E}[x{]}^2\text{\hspace{1em}(1.40)}$$

协方差表示随机变量x和y的共同变化程度。如果x和y独立，则协方差为0.

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ cov[x, y] &=& …
如果是两个随机向量的情况

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ cov[x, y] &=& …

1.2.3 贝叶斯概率

贝叶斯定理:

$$p(w|D)=\frac{p(D|w)p(w)}{p(D)}\text{\hspace{1em}(1.43)}$$

我们可以根据观测到$D$后的后验概率$p(w|D)$来估计$w$的不确定性。贝叶斯定理右侧的量$p(D|w)$由观测到的数据集$D$来估计，可以被看成参数向量$w$的似然函数（likelihood function）。

不同的参数向量$w$的情况下，观测到的数据集的可能性为似然函数。

注意似然不表示它是$w$的概率分布，它关于$w $的积分也不（一定）等于1。
$$\text{posterior}\propto \text{likelihood}\times \text{prior}\text{\hspace{1em}(1.44)}$$
分母是归一化因子：

$$p(D)=\int p(D|w)P(w)dw\text{\hspace{1em}(1.45)}$$

频率派：w是固定的参数。最小误差函数就是最大似然估计

贝叶斯派：w不是固定的，需要用概率分布表达这种不确定性。

1.2.4 高斯分布

对于一元变量:

$\mathcal{N}\left(x | \mu, \sigma^{2}\right)=\frac{1}{\left(2 \pi \sigma^{2}\right){\frac{1}{2}}} \exp \left{-\frac{1}{2 \sigma^{2}}(x-\mu){2}\right} \tag{1.46} $

满足：

$$\mathcal{N}(x|\mu ,{\sigma }^2)>0\text{\hspace{1em}(1.47)}$$

$${\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)dx=1\text{\hspace{1em}(1.48)}$$

期望为：

$$\mathbb{E}[x]={\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)xdx=\mu \text{\hspace{1em}(1.49)}$$

$$\mathbb{E}[x^2]={\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)x^{2}dx={\mu }^2+{\sigma }^2\text{\hspace{1em}(1.50)}$$

方差为：

$$var[x]=\mathbb{E}[x^2]-\mathbb{E}[x{]}^2={\sigma }^2\text{\hspace{1em}(1.51)}$$

当x是d维向量：

$$\mathcal{N}(x|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\Sigma {|}^{1/2}}exp-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\text{\hspace{1em}(1.52)}$$

参考资料：

https://blog.csdn.net/qq_37549266/article/details/95942282

https://www.zhihu.com/question/36339816

当我们进行D次观测。每次取样都是相同的的高斯分布中取样，只是我们不知道期望和方差。独立同分布i.i.d的取样。

数据集的概率为:

$$p(X|\mu ,{\sigma }^2)=\prod _{n=1}^{N}N(x_n|\mu ,{\sigma }^2)\text{\hspace{1em}(1.53)}$$

希望可以通过最大似然来求解未知的期望和方差。取对数方便计算

$$\ln p(x|\mu ,{\sigma }^2)=-\frac{1}{2{\sigma }^2}\sum _{n=1}^N(x_n-\mu {)}^2-\frac{N}{2}\ln {\sigma }^2-\frac{N}{2}\ln (2\pi )\text{\hspace{1em}(1.54)}$$

样本均值:

$${\mu }_{ML}=\frac{1}{N}\sum _{n=1}^N{x}_n\text{\hspace{1em}(1.55)}$$
样本方差:

$${\sigma }_{ML}^2=\frac{1}{N}\sum _{n=1}^N(x_n-{\mu }_{ML}{)}^2\text{\hspace{1em}(1.56)}$$

当我们用样本的期望和方差来代替原本的期望和方差的时候，期望不会有偏差

KaTeX parse error: \tag works only in display equations

方差会出现偏差。

$$\mathbb{E}\left[{\sigma }_{ML}^2\right]=\left(\frac{N-1}{N}\right){\sigma }^2\text{\hspace{1em}(1.58)}$$

为了得到无偏估计:

$${\sigma }^2=\frac{N}{N-1}{\sigma }_{ML}^2=\frac{1}{N-1}\sum _{n=1}^N(x_n-{\mu }_{ML}{)}^2\text{\hspace{1em}(1.59)}$$

参考资料：https://www.zhihu.com/question/20099757

1.2.5 重新考察曲线拟合

N个输入$ X = (x_1,…,x_N)^T $和输出$ T = (t_1,…,t_N)^T $，在新的输入下求输出。假设t服从$ y(x, w) $相同均值的高斯分布。

$$p(t|x,w,\beta )=\mathcal{N}(t|y(x,w),{\beta }^{-1})\text{\hspace{1em}(1.60)}$$

我们定义的分布的方差的逆为精度-参数$\beta $。

通过最大似然来确定未知参数$ w, \beta $，似然函数为：

$$p(T|X,w,\beta )=\prod _{n=1}^N\mathcal{N}(t_n|y(x_n,w),{\beta }^{-1})\text{\hspace{1em}(1.61)}$$

取对数

$$\ln p(T|X,w,\beta )=-\frac{\beta }{2}\sum _{n=1}^N\{y(x_n,w)-t_n{\}}^2+\frac{N}{2}\ln \beta -\frac{N}{2}\ln (2\pi )\text{\hspace{1em}(1.62)}$$

多项式系数的最大似然解，记作$ w_{ML} $。就是最小化误差函数。而精度等于：

$$\frac{1}{{\beta }_{ML}}=\frac{1}{N}\sum _{n=1}^N{y(x_x,w_{ML})-t_n}^2\text{\hspace{1em}(1.63)}$$

带入1.60就是结果

$$p(t|x,w_{ML},{\beta }_{ML})=\mathcal{N}(t|y(x,w_{ML}),{\beta }_{ML}^{-1})\text{\hspace{1em}(1.64)}$$

引入w的先验:

$$p(\mathbf{w}|\alpha )=\mathcal{N}\left(\mathbf{w}|0,{\alpha }^{-1}\mathbf{I}\right)={\left(\frac{\alpha }{2\pi }\right)}^{\frac{M+1}{2}}\exp \left\{-\frac{\alpha }{2}{\mathbf{w}}^T\mathbf{w}\right\}\text{\hspace{1em}(1.65)}$$

这里有超参数$ \alpha $控制先验分布。利用贝叶斯定理可以得到。
$$p(w|X,T,\alpha ,\beta )\propto p(T|X,w,\beta )p(w|\alpha )\text{\hspace{1em}(1.66)}$$

最大后验MAP就是最大化1.66。取-ln我们可以得到最大后验等价于下面的式子

$$\frac{\beta }{2}\sum _{n=1}^N\{y(x_n,w)-t_n{\}}^2+\frac{\alpha }{2}{w}^{T}w\text{\hspace{1em}(1.67)}$$
就是有正则化项的误差函数。

1.2.6 贝叶斯曲线拟合

上一节我们还是引入了w，并对w进行估计，这不是完全的贝叶斯方法。这节我们对w积分，这是贝叶斯方法的核心。

我们希望的是应用训练集合(X,T)，在已知新的数据x的情况下得到目标值t的概率分布:

$$p(t|x,X,T)=\int p(t|x,w)p(w|X,T)dw\text{\hspace{1em}(1.68)}$$

其实这个积分也是可以求解的，解为：

$$p(t|x,X,T)=\mathcal{N}(t|m(x),s^2(x))\text{\hspace{1em}(1.69)}$$

$$m(x)=\beta \varphi (x{)}^{T}S\sum _{n=1}^N\varphi \left(x_n\right)t_n\text{\hspace{1em}(1.70)}$$

$$s^2(x)={\beta }^{-1}+\varphi (x{)}^T\mathbf{S}\varphi (x)\text{\hspace{1em}(1.71)}$$

$$S^{-1}=\alpha I+\beta \sum _{n=1}^N\varphi (x_n)\varphi (x{)}^T\text{\hspace{1em}(1.72)}$$

其中$ I $是单位矩阵，定义向量$\phi(x) $为$ \phi_i(x) = x^i, i = 0,…,M $。

剩余证明：https://www.cnblogs.com/wacc/p/5495448.html

参考资料：https://qiita.com/gucchi0403/items/bfffd2586272a4c05a73

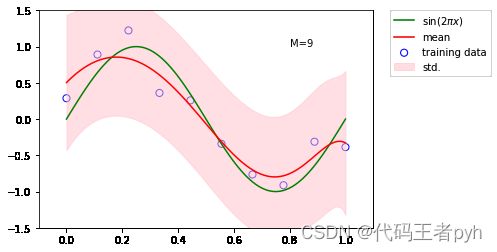
# 贝叶斯曲线拟合
model = BayesianRegression(alpha=2e-3, beta=2)
model.fit(X_train, y_train)

y, y_err = model.predict(X_test, return_std=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="mean")
plt.fill_between(x_test, y - y_err, y + y_err, color="pink", label="std.", alpha=0.5)
plt.xlim(-0.1, 1.1)
plt.ylim(-1.5, 1.5)
plt.annotate("M=9", xy=(0.8, 1))
plt.legend(bbox_to_anchor=(1.05, 1.), loc=2, borderaxespad=0.)
plt.show()

1.3 模型选择

我们训练出了很多模型，因为可能发生过拟合，我们需要正则化。也需要一个判断泛化性能好坏的标准。一般用一个未参与训练的测试集，进行交叉验证。

对所有模型的优劣求平均。如果留出的数据只有一个就是留一验证。但缺点：

1.训练次数随着分割的变细而增加，时间成本增加。

2.参数太多，参数的组合甚至是指数型增加，我们如何选择测试集。

我们模型是由训练数据而决定的，不是参数的选择而决定。

赤池信息准则AIC akaike information criterion：

$$\ln p(D|w_{ML})-M\text{\hspace{1em}(1.73)}$$

这里的$ p(D|w_{ML}) $是最合适的对数似然函数，$ M $是模型中的可调节参数。之后还有BIC。

1.4维度灾难

高维数据数据难区分。

一种解法就是划分成小格子，格子里多的点就是这个区域的点。但划分个数随参数的维度增加激增。

推广到曲线拟合上。我们有D个输入变量，一个三阶多项式系数随着D的增加是幂增加。

$$y(x,w)=w_0+\sum _{i=1}^D{w}_i{x}_i+\sum _{i=1}^D\sum _{j=1}^D{w}_{ij}{x}_i{x}_j+\sum _{i=1}^D\sum _{j=1}^D\sum _{k=1}^D{w}_{ijk}{x}_i{x}_j{x}_k\text{\hspace{1em}(1.74)}$$

这里是系数的个数正比于$ D^3 $。M阶多项式就正比于$ D^M $了。

高维到底会产生什么效果。比方说一个D维空间的半径r=1的球体。$ r = 1 − \epsilon $和半径$r = 1 $之间的部分占球的总体积的百分比是多少。

$$V_D(r)=K_D{r}^D\text{\hspace{1em}(1.75)}$$

$$\frac{V_D(1)-V_D(1-ϵ)}{V_D(1)}=1-(1-ϵ{)}^D\text{\hspace{1em}(1.76)}$$

因此，在高维空间中，一个球体的大部分体积都聚集在表面附近的薄球壳上!

不是所有在低维空间的直觉都可以推广到 高维空间。

即便如此，我们依然要使用高维度的数据。真实数据两个特点：1.目标受限在较低有效维度的空间》输入复杂的图片，但目标只是区分简单的任务。2.局部比较光滑，不会突变》空隙部分用插值估计。

1.5决策论

医学诊断，我们给病人拍了X光片，来诊断他是否得了癌症。

输入向量$ x $是X光片的像素的灰度值集合，输出变量$ t $表示病人患有癌症，记作类$ C_1 $或者不患癌症，记作类$ C_2 $。实际中，我们可能二元变量（如：$ t = 0 $来表示$ C_1 $类，$t = 1 $来表示$ C_2 $类）来表示。

希望得到$ p(C_k|x) $。使用贝叶斯方法这些概率可以表示为：

$ p(C_k|x) = \frac{p(x|C_k)p(C_k)}{p(x)} \tag{1.77} $

$ p(C_1) $表示在拍X光片前病人患有癌症的概率，同样的，$ p(C_1|x) $表示获得X光片信息后使用贝叶斯定理修正的后验概率。

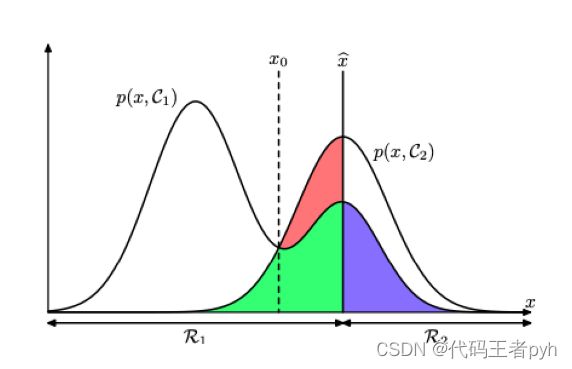
1.5.1 最小化错误分类率

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ p(mistake) &=&…

对于$ x $如果$p(x, C_1) > p(x, C_2) $，那么就把$ x $分到类$ C_1 $中。

对于更一般的K 类的情形,计算正确率会更简单。KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ p(correct) &=&…

1.5.2 最小化期望损失

真实分类是$C_k$,实际分类是$C_j$.定义损失矩阵：

损失函数变为$$\mathbb{E}[L]=\sum _k\sum _j{\int }_{R_j}{L}_{kj}p(x,C_k)dx\text{\hspace{1em}(1.80)}$$

消去共同因子P(x)，根据决策规则就是对于每个新的x，使它分到能使得下式取得最小值的j类。
$$\sum _k{L}_{kj}p(C_k|x)$$

1.5.3拒绝选项

引入$\theta$,低于$\theta$的后验概率$ p(C_k|x) $进行进一步检测或交给专家。

1.5.4推断和决策

三种方法：

1.生成模型:通过对每个类别$C_k $，独立的确定类别的条件密度$ p(x | C_k) $来解决推断问题，还分别推断出类别的先验概率$　p(C_k) $，然后使用贝叶斯定理：

$ p(C_k|x) = \frac{p(x|C_k)p(C_k)}{p(x)} \tag{1.82} $

来计算类别的后验概率$ p(C_k|x) 。 < p > 2. 判 别 模 型 ， 解 决 确 定 类 别 的 后 验 密 度 。

2.判别模型，解决确定类别的后验密度 。<p>2.判别模型，解决确定类别的后验密度p(C_k|x) $的推断问题，然后，使用决策论来对新的输入$ x 进 行 分 类 。 < p > 3. 判 别 函 数 ： 找 到 能 直 接 把 输 入 进行分类。

3.判别函数：找到能直接把输入 进行分类。<p>3.判别函数：找到能直接把输入 x $映射到类别标签$ f(x) $。

一般都需要后验概率：

• 最小化风险：损失矩阵可能会修改
• 拒绝选项：可以设定拒绝比例
• 补偿类先验概率：修正样本分布的偏差
• 组合模型：多手段检测。
  $$p(X_I,X_B|C_k)=p(X_I|C_k)p(X_B|C_k)\text{\hspace{1em}(1.84)}$$

  
  条件独立性假设（朴素贝叶斯假设）：（输入独立）

  
  KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ p(C_k|X_I, X_B…

1.5.5回归问题的损失函数

回到曲线拟合，计算平均损失，求期望。

$$\mathbb{E}[L]=\int \int L(t,y(x))p(x,t)dxdt\text{\hspace{1em}(1.86)}$$

平方误差：

$$\mathbb{E}[L]=\int \int \{y(x)-t{\}}^{2}p(x,t)dxdt\text{\hspace{1em}(1.87)}$$

变分法求解

$$\frac{\delta \mathbb{E}[L]}{\delta y(x)}=2\int \{y(x)-t\}p(x,t)dt=0\text{\hspace{1em}(1.88)}$$

整理：

$$y(x)=\frac{\int tp(x,t)dt}{p(x)}=\int tp(t|x)dt={\mathbb{E}}_t[t|x]\text{\hspace{1em}(1.89)}$$

这就是回归函数：条件$ x $下$ t $的条件均值

另一种方法，看平方项

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ \{y(x) − t\}^2…

带入损失函数。
$$\mathbb{E}[L]=\int \{y(x)-E[t|x]{\}}^{2}p(x)dx+\int var[t|x]p(x)dx\text{\hspace{1em}(1.90)}$$

不同的损失函数，闵可夫斯基函数

$ \mathbb{E}[L_q] = \int\int|y(x) - t|^qp(x,t)dxdt \tag{1.91} $

参考资料:https://qiita.com/ZaKama/items/e172756db6e37fc68d65

1.6 信息论

观测一个离散随机变量x我们得到多少信息。信息量=“惊讶程度”:

被告知小概率事件发生，信息量高；被告知一定会发生的事情，没有信息量。

用h(x)表示，有两个不相关事件x和y，它们的信息量就是它们的和:$h(x,y)=h(x)+h(y)$,对比$p(x,y)=p(x)p(y)$，我们有：

$$h(x)=-lo{g}_{2}p(x)\text{\hspace{1em}(1.92)}$$
负号确保信息一定是非负的，低概率事件》高信息量。

一随机变量的平均信息量:

$$H[x]=-\sum _{x}p(x)lo{g}_{2}p(x)\text{\hspace{1em}(1.93)}$$
叫做随机变量的熵.当p(x)=0,$p(x)lo{g}_{2}p(x)=0$

信息量的实际意义：一个随机变量，8个状态，等可能，熵为：

$$H[x]=-8\times \frac{1}{8}lo{g}_2\frac{1}{8}=3bits$$
如果不是等可能：
$$H[x]=-\frac{1}{2}lo{g}_2\frac{1}{2}-\frac{1}{4}lo{g}_2\frac{1}{4}-\frac{1}{8}lo{g}_2\frac{1}{8}-\frac{1}{16}lo{g}_2\frac{1}{16}-\frac{4}{64}lo{g}_2\frac{1}{64}=2bits$$
非均匀分布比均匀分布的熵要小。

利用非均匀分布这个特点，使用更短的编码来描述更可能的事件，更长的编码来描述不太可能的事件。希望这样做能够得到一个更短的平均编码长度。使用下面的编码串：0、10、110、1110、 111100、111101、111110、111111来表示状态。传输的编码的平均长度就是

$$\text{average code length}=\frac{1}{2}\times 1+\frac{1}{4}\times 2+\frac{1}{8}\times 3+\frac{1}{16}\times 4+4\times \frac{1}{64}\times 6=2bits$$

使用的时候分割就好了：11001110唯一地编码了状态序列c, a, d。

物理学上，熵是混乱程度:

考虑一个包含N个颜色不同的物体的集合，这些物体要被分到若干个箱子中，使得第i个箱子中有$ n_i $个物体。考虑把物体分配到箱子中的不同方案的数量。有N种方式选择第一个物体，有(N-1)种方式选择第二个物体，以此类推，总共有$ N! $种方式把N个物体分配到箱子中。

不区分同一个箱子中同样元素的不同排列。箱子就是染缸。在第$ i^{th} $个箱子有$ n_i! $种排列方式。总方案数量为：

$$W=\frac{N!}{{\prod }_i{n}_i!}\text{\hspace{1em}(1.94)}$$
这就是乘数。

熵是缩放后的对数乘数:

$$H=\frac{1}{N}\ln W=\frac{1}{N}\ln N!-\frac{1}{N}\sum _i\ln n_i!\text{\hspace{1em}(1.95)}$$

现在我们考虑在$n_i / N $固定的情况下，$ N \to \infty $使用Stirling’s近似：

$ \ln N! \simeq N\ln N - N \tag{1.96} $

得出：

$$H=-\underset{N\to \infty }{\lim }\sum _i(\frac{n_i}{N})\ln (\frac{n_i}{N})=-\sum _i{p}_i\ln p_i\text{\hspace{1em}(1.97)}$$

如果箱子是X的离散状态$x_i$，X的熵就是:

$$H[p]=-\sum _{i}p(x_i)\ln p(x_i)\text{\hspace{1em}(1.98)}$$

在归一化条件的限制下我们用拉格朗日乘数法得到：

$$H=-\sum _{i}p(x_i)\ln p(x_i)+\lambda (\sum _{i}p(x_i)-1)\text{\hspace{1em}(1.99)}$$
其实可以求得当所有$p(x_i)$相等的时候，取得最大值。而且二阶导数是负的，所以驻点是最大值:

$$\frac{{\partial }^{2}H}{\partial p(x_i)\partial p(x_j)}=-I_{ij}\frac{1}{p_i}\text{\hspace{1em}(1.100)}$$

连续变量，分割$\Delta$宽度的箱子，p(x)连续，根据均值定理可知，一定有个$x_i$:

$${\int }_{i\Delta }^{(i+1)\Delta }p(x)\mathrm{d}x=p\left(x_i\right)\Delta \text{\hspace{1em}(1.101)}$$

这里：$ \sum_ip(x_i)\Delta = 1 $

只要x落在第i个箱子中，我们就把x赋值为$ x_i $。因此观察到值$ x_i $的概率为$ p(x_i )\Delta $。连续分布就可以看作离散分布。
$$H_{\Delta }=-\sum _{i}p(x_i)\Delta \ln (p(x_i)\Delta )=-\sum _{i}p(x_i)\Delta \ln p(x_i)-\ln \Delta \text{\hspace{1em}(1.102)}$$

忽略第二项，当$\Delta$趋近于0，只看第一项变为积分:

$$\underset{\Delta \to 0}{\lim }\left\{-\sum _{i}p\left(x_i\right)\Delta \ln p\left(x_i\right)\right\}=-\int p(x)\ln p(x)\mathrm{d}x\text{\hspace{1em}(1.103)}$$
把它定义为
$$H[\mathbf{x}]=-\int p(\mathbf{x})\ln p(\mathbf{x})\mathrm{d}\mathbf{x}\text{\hspace{1em}(1.104)}$$
这就是微分熵。
$\delta$ 趋近于0,第二项发散。

反映了：具体化一个连续变量需要的比特位。（个人理解是用在$\delta$趋近于0时候，整体的H变得无穷大）

添加三个限制:

$ \int_{-\infty}^{\infty}p(x)dx = 1 \tag{1.105} $

$ \int_{-\infty}^{\infty}xp(x)dx = \mu \tag{1.106} $

KaTeX parse error: \tag works only in display equations

求极值使用拉格朗日乘数:

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ &-& \int_{-\in…
令其导数为零，有：
$$p(x)=exp\{-1+{\lambda }_1+{\lambda }_{2}x+{\lambda }_3(x-\mu {)}^2\}\text{\hspace{1em}(1.108)}$$

代入限制方程有:

$p(x)=\frac{1}{\left(2 \pi \sigma^{2}\right){\frac{1}{2}}} \exp \left{-\frac{1}{2 \sigma^{2}}(x-\mu){2}\right} \tag{1.109} $
得到高斯分布，最大化微分熵分布就是高斯分布。

求高斯分布的微分熵得到:

$$H[x]=\frac{1}{2}\{1+\ln (2\pi {\sigma }^2)\}\text{\hspace{1em}(1.110)}$$

微分熵可以是负的。

对于联合分布p(x,y)，我们已知x的话，确定y需要的附加信息就是$-lnp(y|x)$。平均附加信息就可以写成：

$$H[y|x]=-\int \int p(y,x)\ln p(y|x)dydx\text{\hspace{1em}(1.111)}$$

这就是条件熵。用乘积规则可以得到:

$$H[x,y]=H[y|x]+H[x]\text{\hspace{1em}(1.112)}$$

参考资料:

http://prml.yutorihiro.com/chapter-1/1-35/

https://lkzf.info/math/prml/1/1.6.html

https://www.slideshare.net/alembert2000/prml-chp1-latter

1.6.1相对熵和互信息

有一个未知分布p(x)，我们用近似的分布q(x)对其建模，它们之间的差异（在已知q(x),希望得到p(x),需要的平均附加信息量）为:

$$\begin{array}{rl}\mathrm{K}\mathrm{L}(p\Vert q)& =-\int p(\mathbf{x})\ln q(\mathbf{x})\mathrm{d}\mathbf{x}-\left(-\int p(\mathbf{x})\ln p(\mathbf{x})\mathrm{d}\mathbf{x}\right)\\ & =-\int p(\mathbf{x})\ln \left\{\frac{q(\mathbf{x})}{p(\mathbf{x})}\right\}\mathrm{d}\mathbf{x}\end{array}\text{\hspace{1em}(1.113)}$$

这就是p(x)和q(x)之间的相对熵，也叫做KL散度。不对称的量。

我们要证明$\mathrm{K}\mathrm{L}(p\Vert q)\ge 0$且当且仅当p(x)=q(x)时等号成立。先引入凸函数的概念：

$$f(\lambda a+(1-\lambda )b)\le \lambda f(a)+(1-\lambda )f(b)\text{\hspace{1em}(1.114)}$$

这里$ 0 ≤ \lambda ≤ 1 $。凸函数的性质就是任意两点连线在函数上方。二阶导数处处为正

推广:

$$f\left(\sum _{i=1}^M{\lambda }_i{x}_i\right)\le \sum _{i=1}^M{\lambda }_{i}f\left(x_i\right)\text{\hspace{1em}(1.115)}$$

这里$ \lambda_i \geq 0 $$且$$ \sum_i\lambda_i = 1 $，叫做Jensen不等式。

如果把$\lambda$的取值当作概率分布：

$$f(\mathbb{E}[x])\le \mathbb{E}[f(x)]\text{\hspace{1em}(1.116)}$$

对于连续变量的Jensen不等式:

$$f\left(\int xp(x)dx\right)\le \int f(x)p(x)dx\text{\hspace{1em}(1.117)}$$

带入1.113KL散度大于等于0得证。

$$\mathrm{K}\mathrm{L}(p\Vert q)=-\int p(\mathbf{x})\ln \left\{\frac{q(\mathbf{x})}{p(\mathbf{x})}\right\}\mathrm{d}\mathbf{x}\ge -\ln \int q(\mathbf{x})\mathrm{d}\mathbf{x}=0$$
利用了-lnx是凸函数的性质。

因为我们不知道p(x)的分布，用$q(x|\theta )$，想计算KL散度，可以用采样的方式，找到训练点$x_n$个，期望可以用加和计算（参考1.35公式）:

$$KL(p||q)\simeq \sum _{n=1}^N\{-\ln q(x_n|\theta )+\ln p(x_n)\}/N\text{\hspace{1em}(1.119)}$$
看到第二项和 $\theta $无关，第一项是$\theta$负对数的似然函数。最小化KL散度就相当于最大化似然函数。

两个变量x,y如果变量不是独立的，我们通过计算联合概率和边缘概率乘积的KL散度，来判断是否接近独立。

KaTeX parse error: No such environment: eqnarray at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲ I[x,y] &\equiv…

这是x和y的互信息。也是大于等于零的，在x=y的时候等号成立。利用概率加和和乘积规则:

$$I[x,y]=H[x]-H[x|y]=H[y]-H[y|x]\text{\hspace{1em}(1.121)}$$

互信息表示一个新的观测y造成的x的不确定性的减小

参考文献

Bishop, Christopher M. (2006). Pattern recognition and machine learning. New York :Springer

https://github.com/jiangyiqun233/PRML_learning
https://space.bilibili.com/6293151?spm_id_from=333.337.0.0