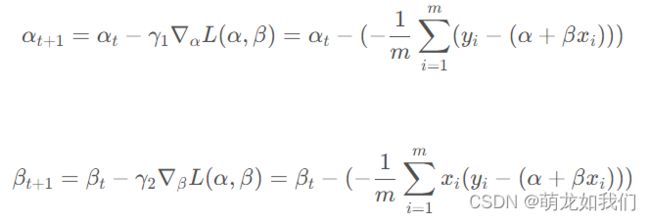学习笔记：机器学习之回归

 活动地址：CSDN21天学习挑战赛

1 简介

        生活中有很多简单的回归问题，比如某两个变量之间存在显著的线性关系，我们可以用回归来量化分析问题，预测变量。

        比如本例子中，我们探究车速和刹车位移之间的关系。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
cars=pd.read_csv("../data/cars.csv",usecols=["speed","dist"])
cars[:5]#speed为车速，dist为刹车距离，

0	4	2
1	4	10
2	7	4
3	7	22
4	8	16

查看数据的情况

x=cars["speed"]
y=cars["dist"]
plt.title("fig1.Scatter plot of vehicle speed and braking distance")
plt.scatter(x,y,marker="*",c='red')

​

 从图像中我们可以看出两个变量大致存在某种线性关系，接下来我们通过建立回归模型去量化它。

2 回归模型

我们的目的是求出下列函数的参数

        

其中x为车速，y为刹车距离。

我们需要建立一个函数去衡量预测值和真实值之间的差距大小，这样才能知道我们最后获得的参数的效果如何。

损失函数为：

​

 n为样本数量，为某次刹车的真实值，为预测值。

自然地，我们需要L达到最小值，这样获得的回归模型才是最精确的，以下有两种方式。

3 两种求解方式

3.1 直接法

使用直接法可以直接求出最优解，但是需要满足损失函数为凸函数，解为解析解。

【函数的凹凸性】

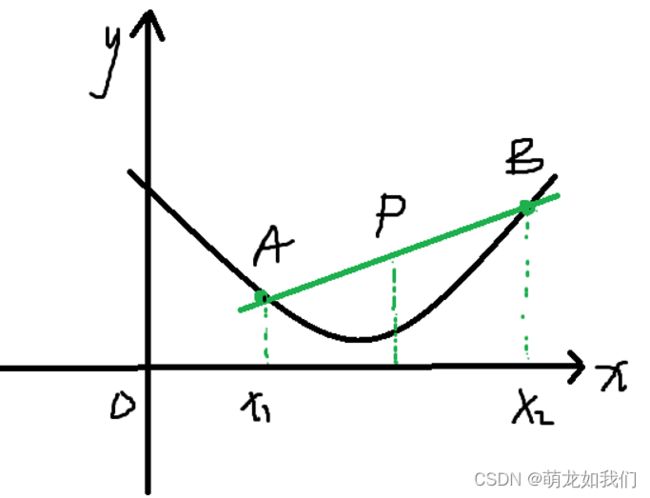
设一个函数为f(x),图像上有两点,弦AB上一点为。

​

则弦AB的方程为：

其中,则.弦AB的参数方程为：

因为f(x)上任A,B所在弦上一点P的函数值大于再f(x)上的函数值，则有：

参数的计算方法参考博客：最小二乘法

实验部分：

import sympy 
#设方程为y=ax+b
#回归系数:比例系数a和偏置值b
a,b=sympy.symbols("a b")
L=0.5*np.sum((y-a*x-b)**2)

#求偏导
f1=sympy.diff(L,b)
f2=sympy.diff(L,a)
print(sympy.diff(L,a))
print(sympy.diff(L,b))

ans=sympy.solve([f1,f2],[b,a])
# 所解得{b: -17.5790948905109, a: 3.93240875912409}

alpha=ans[a]
beta=ans[b]
pre=alpha*x+beta
plt.title("Fig2 Fitting results")
plt.scatter(x,y,c="red")
plt.plot(x,pre,c="green")
plt.show()

绘制所得到的直线：

​

则函数关系为：

3.2 迭代法

        直接对损失函数进行优化师有局限性的，若损失函数为非凸函数的话很难求出最优解。故此提出迭代法，与之前学习的神经网络的后向传播算法类似，通过不断小幅度更新参数来实现损失值最小化。所以，迭代法与直接法不同之处在于参数的更新方式：前者可以通过直接计算得到，而后者需要经过小批量梯度下降的方式去更新。

此时损失函数为：    

​

​为批量大小

目标求解：​

参数更新：​为学习率

​

实验部分：

import  random

#变量更新函数
def update_var(pre_alpha,pre_beta,y,x,lr):
    n=len(x)
    diff_alpha=np.sum(-(y-pre_beta*x-pre_alpha))/n
    diff_beta =np.sum(-x*(y-pre_beta*x-pre_alpha))/n
    new_alpha=pre_alpha-lr*diff_alpha
    new_beta=pre_beta-lr*diff_beta
    
    return (new_alpha,new_beta)

#实现迭代过程
def iterative_func(y,x,raw_alpha,raw_beta,lr,num,sample_num):
    alpha_list = []
    beta_list = []
    alpha = raw_alpha
    beta = raw_beta
    num_list = list(range(1, len(y)+1))
    for i in range(num):
        alpha_list.append(alpha)
        beta_list.append(beta)
        random.shuffle(num_list)
        index = num_list[:sample_num]
        alpha, beta = update_var(alpha, beta,y[index], x[index], lr)
        print("【{}】Now alpha:{},beta:{}".format(i,alpha,beta))
    return (alpha_list, beta_list)

#随机初始化alpha和beta
raw_alpha=np.random.random()*10
raw_beta =np.random.random()*10
raw_alpha

#设置超参数：学习率lr=0.005  迭代次数num=2000,sample_num=16
lr = 0.005
num = 10000
sample_num = 16
alpha_list, beta_list = iterative_func(y, x, raw_alpha, raw_beta,
lr, num,sample_num)

print("after {} times iteration:alpha: {}, beta:{}".format(num,alpha_list[-1], beta_list[-1]))

after 10000 times iteration:alpha: -17.791370073935074, beta:4.000650060840287

#将参数迭代过程产生的数据持久化
import csv

var_data=zip(alpha_list,beta_list)
with open("../data/20220801_vardata.csv",'w',newline='')as f:
        csv_writer=csv.writer(f)
        csv_writer.writerows(['alpha','beta'])
        csv_writer.writerows(var_data)

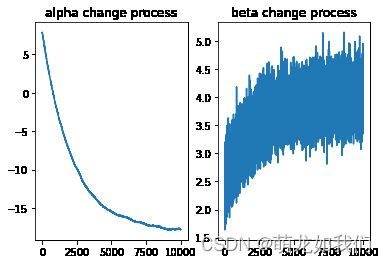
plt.subplot(121)
plt.plot(alpha_list)
plt.title("alpha change process")
plt.subplot(122)
plt.plot(beta_list)
plt.title("beta change process")
plt.show()

参考

(44条消息) 机器学习理论及案例分析(part2)--回归_GoatGui的博客-CSDN博客