排列组合与盒子放球问题
文章目录
-
- 排列组合
-
- 定义
-
- 组合公式
-
- 1.证明 C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m
- 2.证明 C n m C m k = C n k C n − k m − k C_n^mC_m^k=C_n^kC_{n-k}^{m-k} CnmCmk=CnkCn−km−k
- 3.证明 ∑ i = 0 n C n i = 2 n \sum_{i=0}^nC_n^i=2^n ∑i=0nCni=2n
- 4.证明 C n + m k = ∑ i = 0 k C n i × C m k − i C_{n+m}^k=\sum_{i=0}^kC_n^i\times C_{m}^{k-i} Cn+mk=∑i=0kCni×Cmk−i
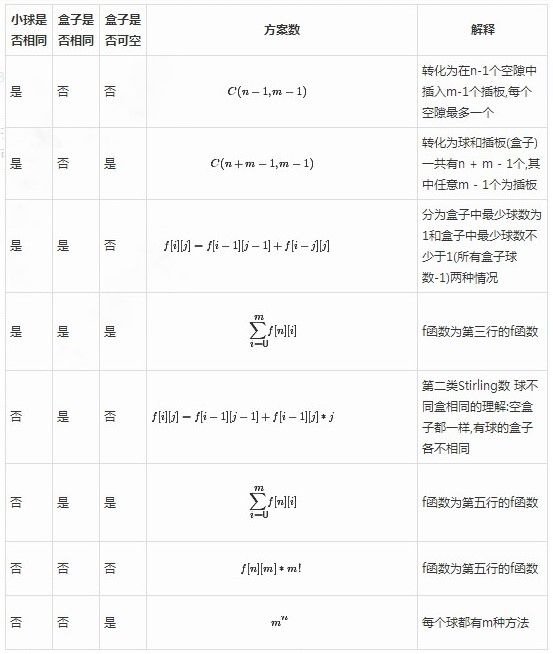
- 盒子放求问题
-
- 1.球相同,盒不同,无空盒
- 2.球相同,盒不同,可以空盒
- 3.球不同,盒相同,无空盒
- 4.球不同,盒相同,可以空盒
- 5.球不同,盒不同,无空盒
- 6.球不同,盒不同,可以空盒
- 7.球相同,盒相同,无空盒
- 8.球相同,盒相同,可以空盒
- 总结
排列组合
定义
排列( A r r a n g e m e n t / P e r m u t a t i o n Arrangement/Permutation Arrangement/Permutation)定义:从 n n n个不同元素中取出 m ( m ≤ n ) m(m≤n) m(m≤n)个元素,按照一定的顺序排成一列,叫做从 n n n个元素中取出 m m m个元素的一个排列。
从 n n n个不同元素中取出 m m m个不同元素,所有不同排列的个数称为排列种数或称排列数,记为 A n m A_n^{m} Anm(排列数旧版记作 P n m P_n^m Pnm,都一样)。
A n m = n × ( n − 1 ) × ( n − 2 ) × ( n − 3 ) × . . . × ( n − m + 1 ) = n ! ( n − m ) ! A_n^m=n\times(n-1)\times(n-2)\times(n-3)\times...\times(n-m+1)=\tfrac{n!}{(n-m)!} Anm=n×(n−1)×(n−2)×(n−3)×...×(n−m+1)=(n−m)!n!
组合( C o m b i n a t i o n Combination Combination)定义:从 n n n个不同的元素中,任取 m ( m ≤ n ) m(m≤n) m(m≤n)个元素为一组,叫作从 n n n个不同元素中取出 m m m个元素的一个组合。
从 n n n个元素中不重复地选取 m m m个元素的一个组合。所有这样的组合的总数称为组合数,记作或 C n m C_n^m Cnm。
C n m = n ! m ! ( n − m ) ! , C n 0 = 1 C_n^m=\tfrac{n!}{m!(n-m)!},C_n^0=1 Cnm=m!(n−m)!n!,Cn0=1
组合公式
1.证明 C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m
C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m
⇒ n ! m ! ( n − m ) ! = n ! ( n − m ) ! ( n − n + m ) ! \Rightarrow \tfrac{n!}{m!(n-m)!}=\tfrac{n!}{(n-m)!(n-n+m)!} ⇒m!(n−m)!n!=(n−m)!(n−n+m)!n!
⇒ n ! m ! ( n − m ) ! = n ! m ! ( n − m ) ! \Rightarrow\tfrac{n!}{m!(n-m)!}=\tfrac{n!}{m!(n-m)!} ⇒m!(n−m)!n!=m!(n−m)!n!
2.证明 C n m C m k = C n k C n − k m − k C_n^mC_m^k=C_n^kC_{n-k}^{m-k} CnmCmk=CnkCn−km−k
C n m C m k = C n k C n − k m − k C_n^mC_m^k=C_n^kC_{n-k}^{m-k} CnmCmk=CnkCn−km−k
⇒ n ! m ! ( n − m ) ! × m ! k ! ( m − k ) ! = n ! k ! ( n − k ) ! × ( n − k ) ! ( m − k ) ! ( n − m ) ! \Rightarrow\tfrac{n!}{m!(n-m)!}\times\tfrac{m!}{k!(m-k)!}=\tfrac{n!}{k!(n-k)!}\times\tfrac{(n-k)!}{(m-k)!(n-m)!} ⇒m!(n−m)!n!×k!(m−k)!m!=k!(n−k)!n!×(m−k)!(n−m)!(n−k)!
⇒ n ! k ! ( n − m ) ! ( m − k ) ! = n ! k ! ( n − m ) ! ( m − k ) ! \Rightarrow\tfrac{n!}{k!(n-m)!(m-k)!}=\tfrac{n!}{k!(n-m)!(m-k)!} ⇒k!(n−m)!(m−k)!n!=k!(n−m)!(m−k)!n!
3.证明 ∑ i = 0 n C n i = 2 n \sum_{i=0}^nC_n^i=2^n ∑i=0nCni=2n
这里我们需要使用二项式展开式。
我们知道:
( a + b ) n = C n 0 a n + C n 1 a n − 1 b + C n 2 a n − 2 b 2 + . . . + C n n b n = ∑ i = 0 n C n i a n − i b i (a+b)^n=C_n^0a^n+C_n^1a^{n-1}b+C_n^2a^{n-2}b^2+...+C_n^nb^n=\sum_{i=0}^nC_n^ia^{n-i}b^i (a+b)n=Cn0an+Cn1an−1b+Cn2an−2b2+...+Cnnbn=∑i=0nCnian−ibi
我们令 a = b = 1 a=b=1 a=b=1
则 2 n = ∑ i = 0 n C n i 2^n=\sum_{i=0}^nC_n^i 2n=∑i=0nCni,得证。
4.证明 C n + m k = ∑ i = 0 k C n i × C m k − i C_{n+m}^k=\sum_{i=0}^kC_n^i\times C_{m}^{k-i} Cn+mk=∑i=0kCni×Cmk−i
我们令:
( 1 + x ) n + m = ( 1 + x ) m × ( 1 + x ) n (1+x)^{n+m}=(1+x)^m\times(1+x)^n (1+x)n+m=(1+x)m×(1+x)n
由上一个定理知:
⇒ ∑ k = 0 n + m C n + m k x k = ∑ i = 0 n C n i x i × ∑ j = 0 m C m j x j \Rightarrow\sum_{k=0}^{n+m}C_{n+m}^kx^k=\sum_{i=0}^nC_n^ix^i\times\sum_{j=0}^mC_m^jx^j ⇒∑k=0n+mCn+mkxk=∑i=0nCnixi×∑j=0mCmjxj
因为左右相等,所以我们 x k x^k xk要对应 x i ∗ x k − i x^i*x^{k-i} xi∗xk−i才行啊。
又因为 x i ∗ x k − i x^i*x^{k-i} xi∗xk−i有 k k k项。
所以:
C n + m k x k = ∑ i = 0 k C n i x i × C m k − i x k − i C_{n+m}^kx^k=\sum_{i=0}^kC_n^ix^i\times C_{m}^{k-i}x^{k-i} Cn+mkxk=∑i=0kCnixi×Cmk−ixk−i
C n + m k x k = ∑ i = 0 k C n i × C m k − i x k C_{n+m}^kx^k=\sum_{i=0}^kC_n^i\times C_{m}^{k-i}x^k Cn+mkxk=∑i=0kCni×Cmk−ixk
两边约掉 x k x^{k} xk后得证。
盒子放求问题
1.球相同,盒不同,无空盒
我们使用隔板法。
这种问题就相当于是:在 n − 1 n-1 n−1个球缝隙之间插入 m − 1 m-1 m−1个隔板,将球分成 n n n份。
所以 a n s = C n − 1 m − 1 ans=C_{n-1}^{m-1} ans=Cn−1m−1。
代码
#include 2.球相同,盒不同,可以空盒
我们就预先在 m m m个盒中加一个虚拟球,然后问题就转换成了第一个问题。
a n s = C n + m − 1 m − 1 ans=C_{n+m-1}^{m-1} ans=Cn+m−1m−1。
代码
#include 3.球不同,盒相同,无空盒
这就是第二类斯特林数:
我们定义 f [ i ] [ j ] f[i][j] f[i][j]为前 i i i个球放入 j j j个盒子的方案数。
我们把这个球放在前 j j j个盒子中,就有 m × f [ i − 1 ] [ j ] m\times f[i-1][j] m×f[i−1][j]种方案。
我们把这个球放在第 j j j个新盒子中,就有 f [ i − 1 ] [ j − 1 ] f[i-1][j-1] f[i−1][j−1]种方案。
所以状态转移方程式为:
f[i][j]=j*f[i-1][j]+f[i-1][j-1];
我们的初始化为:
f[0][0]=1;
代码
#include 4.球不同,盒相同,可以空盒
这道题与第三道很像。
状态转移方程式:
for(int i=1;i<=m;i++) ans+=f[n][i];
我们就分别把 n n n个球放进前 1 1 1个盒子,把 n n n个球放进前 2 2 2个盒子…把 n n n个球放进前 m m m个盒子。
代码
#include 5.球不同,盒不同,无空盒
我们可以看做第三个问题。只是因为盒子不同,所以我们需要将盒子排个序,共有: A m m = m ! ( m − m ) ! = m ! A_m^m=\tfrac{m!}{(m-m)!}=m! Amm=(m−m)!m!=m!
所以 a n s = m ! × f [ n ] [ m ] ans=m!\times f[n][m] ans=m!×f[n][m]
代码
#include 6.球不同,盒不同,可以空盒
每个球都可以选任意盒子,每个球有 m m m种选法,所以 n n n个球就有:
a n s = m n ans=m^n ans=mn。
代码
#include 7.球相同,盒相同,无空盒
我们定义 f [ n ] [ m ] f[n][m] f[n][m]为 n n n个球 m m m个盒子的方案数。
则:
for(int k=1;k<=j;k++)
f[i][j]=(f[i][j]+f[i-j][k])%MOD;
我们先铺 m m m个球分别到 m m m个盒子,然后剩下 n − m n-m n−m个球随便放。
代码
#include 8.球相同,盒相同,可以空盒
我们就放 m m m个虚拟球分别到 m m m个盒子,然后 n n n个球随便放。
代码
#include