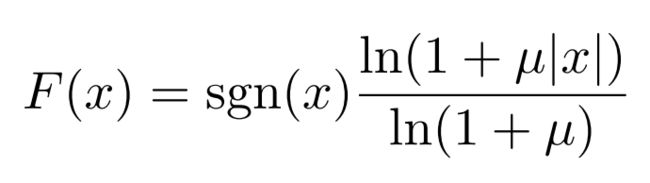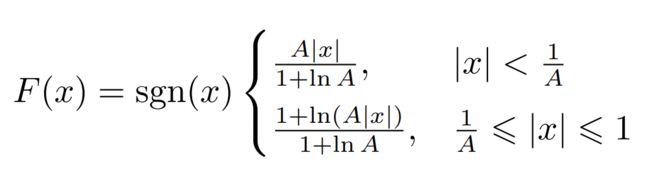音频编码介绍

1. 线性脉冲编码

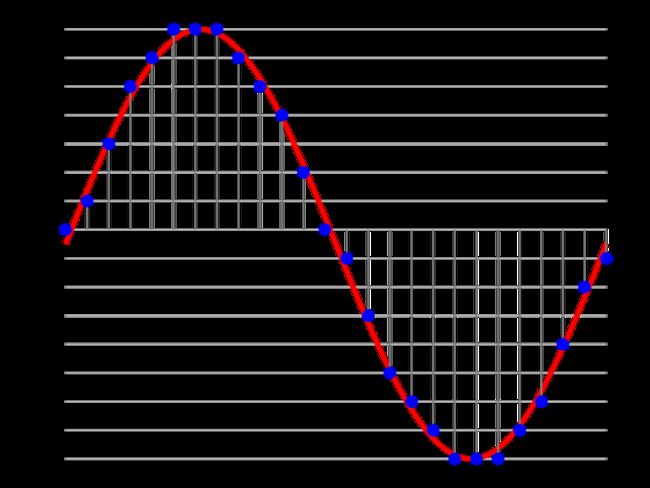
1.1 脉冲编码 pcm

直接将采样过后的振幅进行量化， 此时， 量化后，各个相邻整数 所表示的 信号差值可以是不等的。

1.2 线性脉冲编码

量化时候， 相邻整数所表示的信号的差值 是恒定的， 则是 线性脉冲编码；

2. 非线性脉冲编码

由于人耳对响度非线性感知能力， （响度的物理量是叫做声强， 单位用db 分贝表示）， 对低响度的 声音更敏感；

非线性编码：
对低响度的声音 使用更高的精度；

北美地区 和 中国 使用的是两种，不同的 非线性脉冲编码：

Assume x ∈ [−1,1], sgn(x) is the sign function

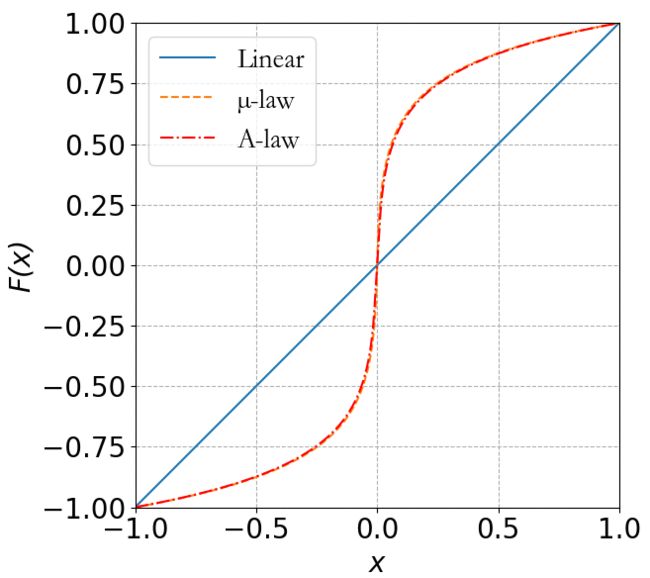
2.1 μ-law (North America, Japan, etc.)

2.2 A-law (China, Europe, etc.)

3. 自适应脉冲编码

Adaptive PCM

由于线性还是非线性编码， 对整个信号采用的都是相同的量化方案， 该量化方案不随时间的改变而变化，

然而现实中， 信号的幅度 是随着时间而变化的，

• 当信号的幅度较大时： 需要覆盖到它；

• 当信号的幅度较小时： 需要更加精准的量化；

所以提出自适应量化：

在量化之前， 我们对某一个局部， 使用局部幅度对其进行归一化。

4. 差分脉冲编码

Differential PCM

之前的编码方式， 都是信号的对采样值 $x[n]$ 直接进行量化，
而各个采样值$x[n]$ 之间的数据差异较大， 量化效果不好；

而差分脉冲编码的思想：

取相邻两个采样值之间的差值 ， 对该差值进行量化， 从而提高量化精度；

原因是相邻采样值之间的差值 通常会远小于这两个采样值本身，
$$e[n]=x[n]-x[n-1]$$

5. 线性预测编码

Linear predictive coding LPC

$$e[n]=x[n]-x[n-1]$$

将上述表达式， 改写成:

$$x[n]=x[n-1]+e[n]$$

将 x[n-1] 替换成 $\hat{x}[n]$ , 得到如下表达式子

$$x[n]=\hat{x}[n]+e[n]$$

其中， $\hat{x}[n]$ 代表了对当前采样值的预测， 该预测值使用前p 个采样值来表示，

$$x[n]=\sum _{i=1}^p{a}_{i}x[n-i]+e[n]$$

其中 $p$ 称为预测阶数 , $a_i$ 称为预测系数；

6. 时域中的其他编码方式

6.1 ADPCM

将上述的自适应 和 差分编码 结合起来，

6.2 增量调制

将上述的预测误差 $e[n]$ 仅使用一个比特进行表示，

$e[n]$ > Δ: quantize to 0
$e[n]$ < −Δ: quantize to 1

6.3 自适应增量调制

Δ 值可以随着时间， 自适应的选取， 而不是固定的时候， 称之为 自适应增量调制。

7. 频域编码方法

前面的方法， 都是对信号在时间域上 进行编码，

此外，我们也可以在频域上， 对信号进行编码：

7.1 子带编码

SBC： sub band coding

该方法先将信号分割成 若干个不同的频带分量，再对每个子频带分量 进行编码。 这种方法 可以采用不同的编码速率 对不同的子频带 进行编码

7.2 自适应 变换域编码

先对语音信号进行某种 正交变换， 对变换系数 进行量化编码，实现更低的 编码速率；

常用的正交变换有 离散余弦变换，