手把手教你深度学习和实战-----逻辑回归算法
系列文章目录
第一章 手把手教你深度学习和实战-----线性回归+梯度下降法
第二章 手把手教你深度学习和实战-----逻辑回归算法
第三章 手把手教你深度学习和实战-----全连接神经网络
第四章 手把手教你深度学习和实战-----卷积神经网络
第五章 手把手教你深度学习和实战-----循环神经网络
文章目录
- 系列文章目录
- 前言
- 1、逻辑回归算法的原理
- 2、损失函数和参数更新
- 总结
前言
在机器学习有监督学习中大致可以分为两大任务，一种是回归任务，一种是分类任务；那么这两种任务的区别是什么呢？按照较官方些的说法,输入变量与输出变量均为连续变量的预测问题是回归问题,输出变量为有限个离散变量的预测问题成为分类问题。
举个例子，输入一个人每日的运动时间、睡眠时间、工作时间、饮食等一些特征来预测一个人的体重，一个人的体重的值可以有无限个值。所以预测的结果是无限的、不确定的连续数值。这样的机器学习任务就是回归任务。
如果利用一个人每日的运动时间、睡眠时间、工作时间、饮食等一些特征来判断这个人的身体状况是否健康，那么最终的判断的结果就只有两种健康和不健康。这样的输出结果为离散值，预测的结果也是一个有限的数值来代表种类。
前面已经对线性回归算法进行了一个讲解。线性回归算法可以解决一些简单的回归任务。而相对于线性回归来说，逻辑回归却是用来解决二分类问题的。因此逻辑回归这个名字很容易让初学者一脸懵，因为名字中带有回归却是用来做分类任务，其中后面深入去学习就会发现逻辑回归其实是用回归的方法来做分类，逻辑回归的本质输出还是一个在0-1之间的连续值，人为设定一个阈值来使输出的值映射为一个类别。下面我们就来具体的看看逻辑回归算法的原理。
1、逻辑回归算法的原理
首先我们来介绍一下sigmoid函数，sigmoid函数的定义如如下： g ( z ) = 1 1 + e − z g(z)= \frac{1}{1+e^{-z}} g(z)=1+e−z1 在sigmoid函数中，公式中,e为欧拉常数，自变量z可以取任意实数，函数的值域为[0，1]，这就相当于将输入的自变量值映射到0-1之间；sigmoid的函数图像如下图所示：
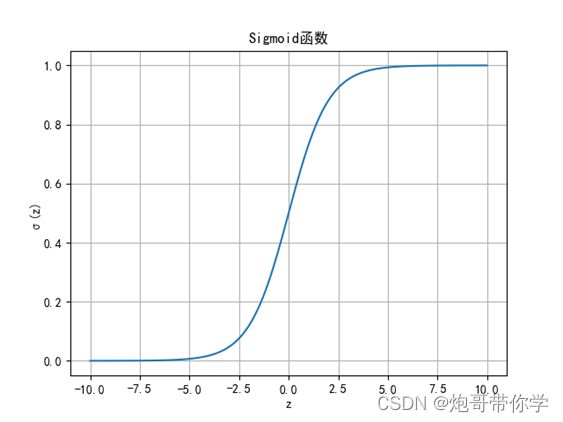我们可以想象一下，一件事发生的概率一定是是在0到1之间。因此我们可以利用输出的值来判断事情发生的概率的大小，假设这时候设置一个阈值0.3，那么当得分大于0.3则为正例，小于0.3则为反例，因此阈值不一定非要是0.5。例如在现实生活中，利用机器学习模型判断一个人是否生病，往往会把阈值设置的较小。因为如果把阈值设为0.5，那么当一个人最后的逻辑回归的得分为0.49时，其实这个人是有一定可能患病的，那么模型判断其没有患病，其实这样是不负责任的。当阈值设置的小点，即可以进一步进行检测看是否身体有问题，这样即可以保证误判的可能性变小，同时也可以帮助筛掉一些身体健康的人，提升医生治病的效率。
下面我们将函数的自变量转化为利用输入的数据特征来表示，以此来利用sigmoid函数对其进行映射。 z = w 0 x 0 + w 1 x 1 + + w n x n + b z = W ⊤ X + b \begin{gathered} z=w_0 x_0+w_1 x_1++w_n x_n+b \\ z=W^{\top} X+b \end{gathered} z=w0x0+w1x1++wnxn+bz=W⊤X+b 此时自变量就转变成输入的数据特征了，特征利用向量X表示。同时特征还有对应的权重参数向量W来表示这个数据特征的重要程度,同时还有偏置参数b。因此，逻辑回归模型可以用如下的公式来表达： g ( X ) = 1 1 + e − w T X + b g(X)=\frac{1}{1+e^{-w^T X+b}} g(X)=1+e−wTX+b1 因此，将数据的特征输入到逻辑回归模型中，就可以计算出该事件为正例的概率。因此对于一个二分类的的问题，此时正例和反例的函数表达式就如下式所示：
预测结果为正例的表达式： p ( y = 1 ∣ X ) = 1 1 + e − w T X + b p(y=1 \mid X)=\frac{1}{1+e^{-w^T X+b}} p(y=1∣X)=1+e−wTX+b1 预测结果为反例的表达式： p ( y = 0 ∣ X ) = e − w T X + b 1 + e − w T X + b = 1 − p ( y = 1 ∣ X ) p(y=0 \mid X)=\frac{e^{-w^T X+b}}{1+e^{-w^T X+b}}=1-p(y=1 \mid X) p(y=0∣X)=1+e−wTX+be−wTX+b=1−p(y=1∣X) 上面的式子可以统一表达当案例为正例和反例的两种情况，例如：
为正例的时候，也就是当y=1的时候，将y=1带入到上式，可以得到： p ( 1 ∣ X ) = p ( y = 1 ∣ X ) = 1 1 + e − w T X + b p(1 \mid X)=p(y=1 \mid X)=\frac{1}{1+e^{-w^T X+b}} p(1∣X)=p(y=1∣X)=1+e−wTX+b1 为反例的时候，也就是当y=0的时候，将y=0带入到上式，可以得到： p ( 0 ∣ X ) = 1 − p ( y = 1 ∣ X ) = e − w T X + b 1 + e − w T X + b p(0 \mid X)=1-p(y=1 \mid X)=\frac{e^{-w^T X+b}}{1+e^{-w^T X+b}} p(0∣X)=1−p(y=1∣X)=1+e−wTX+be−wTX+b 因此，很显然这个公式可以将正反两种情况都考虑到，同时也方便后续的求解和推导。
2、损失函数和参数更新
前面的逻辑回归模型也有了，利用该模型可以对输入的数据特征进行分类判断。但是模型的判断能力的好坏取决于模型中的参数w和b，因此我们需要从提供的数据样本中不断学习，从而更新参数w和b使得预测出的结果全部正确的概率最大，简单来讲就是所有的样本的预测正确的概率相乘得到数值是最大的，按这样的要求得到数据表达式如下所示，该式就是逻辑回归的损失函数。
L ( w , b ) = ∏ i = 1 m ( P ( 1 ∣ x i ) ) y i ( 1 − P ( 1 ∣ x i ) ) 1 − y i L(w, b)=\prod_{i=1}^m\left(P\left(1 \mid x_i\right)\right)^{y_i}\left(1-P\left(1 \mid x_i\right)\right)^{1-y_i} L(w,b)=i=1∏m(P(1∣xi))yi(1−P(1∣xi))1−yi 其中： P ( 1 ∣ x i ) = g ( x i ) = 1 1 + e − w T x i + b P\left(1 \mid x_i\right)=g\left(x_i\right)=\frac{1}{1+e^{-w^T x_i+b}} P(1∣xi)=g(xi)=1+e−wTxi+b1 但是我们习惯将sigmoid函数按如下的形式撰写： g ( x i ) = 1 1 + e − w T x i + b = σ ( w ⊤ x i + b ) g\left(x_i\right)=\frac{1}{1+e^{-w^T x_i+b}}=\sigma\left(w^{\top} x_i+b\right) g(xi)=1+e−wTxi+b1=σ(w⊤xi+b) 因此就可以将上述的损失函数写成如下所示： L ( w , b ) = ∏ i = 1 m ( σ ( w ⊤ x i + b ) ) y i ( 1 − σ ( w ⊤ x i + b ) ) 1 − y i ψ L(w, b)=\prod_{i=1}^m\left(\sigma\left(w^{\top} x_i+b\right)\right)^{y_i}\left(1-\sigma\left(w^{\top} x_i+b\right)\right)^{1-y_i} \psi L(w,b)=i=1∏m(σ(w⊤xi+b))yi(1−σ(w⊤xi+b))1−yiψ 相对连乘运算，连加运算计算起来要比连乘要简单许多，因此可以利用两边同时取log的形式让连乘变成连加。此时就变成如下式所示： l ( w , b ) = log L ( w , b ) = ∑ i = 1 m ( y i log σ ( w ⊤ x i + b ) + ( 1 − y i ) log ( 1 − σ ( w ⊤ x i + b ) ) ) l(w, b)=\log L(w, b)=\sum_{i=1}^m\left(y_i \log \sigma\left(w^{\top} x_i+b\right)+\left(1-y_i\right) \log \left(1-\sigma\left(w^{\top} x_i+b\right)\right)\right) l(w,b)=logL(w,b)=i=1∑m(yilogσ(w⊤xi+b)+(1−yi)log(1−σ(w⊤xi+b))) 此时我们只需要找到一组参数w和b使得 l ( w , b ) l(w, b) l(w,b)最大即可，但是在机器学习中通常希望把上升问题转化为下降问题，因此将该函数取相反数即可。得到下式： J ( w , b ) = − 1 m l ( w , b ) J_{(w, b)}=-\frac{1}{m} l(w, b) J(w,b)=−m1l(w,b) 经过推导 J ( w , b ) J_{(w, b)} J(w,b)这个函数就是逻辑回归最终的损失函数,我们叫它交叉熵损失函数。
此时，只要利用梯度下降法进行参数更新就能通过数据样本不断学习更新参数了，梯度下降法的步骤如下：
步骤1，利用损失函数求解对应参数的偏导数：
w参数的偏导数的计算步骤如下所示： ∂ J ( w , b ) ∂ w = − 1 m ∑ i = 1 m ∂ ( y i log σ ( ω ⊤ x i + b ) + ( 1 − y i ) log ( 1 − σ ( ω ⊤ x i + b ) ) ∂ w = − 1 m ∑ i = 1 m y i σ ( ω ⊤ x i + b ) [ 1 − σ ( ω ⊤ x i + b ) ] σ ( ω ⊤ x i + b ) x i + ( 1 − y i ) − σ ( ω ⊤ x i + b ) [ 1 − σ ( ω ⊤ x i + b ) ] 1 − σ ( ω ⊤ x i + b ) x i = − 1 m ∑ i = 1 m y i x i − σ ( w ⊤ x i + b ) x i = 1 m ∑ i = 1 m ( σ ( w ⊤ x i + b ) − y i ) x i \begin{gathered} \frac{\partial J_{(w, b)}}{\partial w}=-\frac{1}{m} \sum_{i=1}^m \frac{\partial\left(y_i \log \sigma\left(\omega^{\top} x_i+b\right)+\left(1-y_i\right) \log \left(1-\sigma\left(\omega^{\top} x_i+b\right)\right)\right.}{\partial w} \\ =-\frac{1}{m} \sum_{i=1}^m y_i \frac{\sigma\left(\omega^{\top} x_i+b\right)\left[1-\sigma\left(\omega^{\top} x_i+b\right)\right]}{\sigma\left(\omega^{\top} x_i+b\right)} x_i \\ +\left(1-y_i\right) \frac{-\sigma\left(\omega^{\top} x_i+b\right)\left[1-\sigma\left(\omega^{\top} x_i+b\right)\right]}{1-\sigma\left(\omega^{\top} x_i+b\right)} x_i \\ =-\frac{1}{m} \sum_{i=1}^m y_i x_i-\sigma\left(w^{\top} x_i+b\right) x_i \\ =\frac{1}{m} \sum_{i=1}^m\left(\sigma\left(w^{\top} x_i+b\right)-y_i\right) x_i \end{gathered} ∂w∂J(w,b)=−m1i=1∑m∂w∂(yilogσ(ω⊤xi+b)+(1−yi)log(1−σ(ω⊤xi+b))=−m1i=1∑myiσ(ω⊤xi+b)σ(ω⊤xi+b)[1−σ(ω⊤xi+b)]xi+(1−yi)1−σ(ω⊤xi+b)−σ(ω⊤xi+b)[1−σ(ω⊤xi+b)]xi=−m1i=1∑myixi−σ(w⊤xi+b)xi=m1i=1∑m(σ(w⊤xi+b)−yi)xi 最终 ∂ J ( w , b ) ∂ w \frac{\partial J_{(w, b)}}{\partial w} ∂w∂J(w,b)的计算结果如下： ∂ J ( w , b ) ∂ w = 1 m ∑ i = 1 m ( σ ( w ⊤ x i + b ) − y i ) x i \frac{\partial J_{(w, b)}}{\partial w}=\frac{1}{m} \sum_{i=1}^m\left(\sigma\left(w^{\top} x_i+b\right)-y_i\right) x_i ∂w∂J(w,b)=m1i=1∑m(σ(w⊤xi+b)−yi)xi b参数的偏导数的计算步骤如下所示： ∂ J ( w , b ) ∂ b = − 1 m ∑ i = 1 m ∂ ( y i log σ ( ω ⊤ x i + b ) + ( 1 − y i ) log ( 1 − σ ( ω ⊤ x i + b ) ) ∂ b = − 1 m ∑ i = 1 m y i σ ( ω ⊤ x i + b ) [ 1 − σ ( ω ⊤ x i + b ) ] σ ( ω ⊤ x i + b ) + ( 1 − y i ) − σ ( ω ⊤ x i + b ) [ 1 − σ ( ω ⊤ x i + b ) ] 1 − σ ( ω ⊤ x i + b ) = − 1 m ∑ i = 1 m y i [ 1 − σ ( ω ⊤ x i + b ) ] + ( y i − 1 ) σ ( ω ⊤ x i + b ) = 1 m ∑ i = 1 m σ ( ω ⊤ x i + b ) − y i \begin{gathered} \frac{\partial J_{(w, b)}}{\partial b}=-\frac{1}{m} \sum_{i=1}^m \frac{\partial\left(y_i \log \sigma\left(\omega^{\top} x_i+b\right)+\left(1-y_i\right) \log \left(1-\sigma\left(\omega^{\top} x_i+b\right)\right)\right.}{\partial b} \\ =-\frac{1}{m} \sum_{i=1}^m y_i \frac{\sigma\left(\omega^{\top} x_i+b\right)\left[1-\sigma\left(\omega^{\top} x_i+b\right)\right]}{\sigma\left(\omega^{\top} x_i+b\right)} \\ +\left(1-y_i\right) \frac{-\sigma\left(\omega^{\top} x_i+b\right)\left[1-\sigma\left(\omega^{\top} x_i+b\right)\right]}{1-\sigma\left(\omega^{\top} x_i+b\right)} \\ =-\frac{1}{m} \sum_{i=1}^m y_i\left[1-\sigma\left(\omega^{\top} x_i+b\right)\right]+\left(y_i-1\right) \sigma\left(\omega^{\top} x_i+b\right) \\ =\frac{1}{m} \sum_{i=1}^m \sigma\left(\omega^{\top} x_i+b\right)-y_i \end{gathered} ∂b∂J(w,b)=−m1i=1∑m∂b∂(yilogσ(ω⊤xi+b)+(1−yi)log(1−σ(ω⊤xi+b))=−m1i=1∑myiσ(ω⊤xi+b)σ(ω⊤xi+b)[1−σ(ω⊤xi+b)]+(1−yi)1−σ(ω⊤xi+b)−σ(ω⊤xi+b)[1−σ(ω⊤xi+b)]=−m1i=1∑myi[1−σ(ω⊤xi+b)]+(yi−1)σ(ω⊤xi+b)=m1i=1∑mσ(ω⊤xi+b)−yi 最终 ∂ J ( w , b ) ∂ b \frac{\partial J(w, b)}{\partial b} ∂b∂J(w,b)的计算结果如下： ∂ J ( w , b ) ∂ b = 1 m ∑ i = 1 m σ ( ω ⊤ x i + b ) − y i \frac{\partial J_{(w, b)}}{\partial b}=\frac{1}{m} \sum_{i=1}^m \sigma\left(\omega^{\top} x_i+b\right)-y_i ∂b∂J(w,b)=m1i=1∑mσ(ω⊤xi+b)−yi 步骤2，利用计算好的偏导数进行参数更新： w = w − α ∂ J ( w , b ) ∂ w b = b − α ∂ J ( w , b ) ∂ b \begin{aligned} w &=w-\alpha \frac{\partial J_{(w, b)}}{\partial w} \\ b &=b-\alpha \frac{\partial J_{(w, b)}}{\partial b} \end{aligned} wb=w−α∂w∂J(w,b)=b−α∂b∂J(w,b) 步骤3，不断重复步骤1和步骤2，直到损失函数趋于平稳不再下降为止。
按如上的步骤就找到了最合适的模型参数了，利用训练出来的参数就可以进行逻辑回归的分类了。
总结
在机器学习中的两大核心算法，线性回归和逻辑回归分别应用于回归任务和分类任务中。其中最核心的部分就是利用梯度下降法进行参数的更新，梯度下降法体现了模型可以不断利用现有的数据进行不断学习而完成自我更新的过程，因此将线性回归和逻辑回归学好，有利于理解后续的深度学习神经网络算法。因此线性回归和逻辑回归是学习深度学习神经网络必要学好的前置储备知识。