一种速度引导的哈里斯鹰优化算法

一、理论基础

1、哈里斯鹰优化算法

请参考这里。

2、速度引导的哈里斯鹰优化算法

通过嵌入速度引导的位置搜索公式、非线性逃逸能量参数和基于折射反向的学习策略的3种策略对HHO算法进行了改进。

（1）速度引导的位置搜索公式

PSO是Kennedy和Eberhart(1995)提出的一种高效有效的元启发式技术。它的想法来源于鸟类的觅食行为。在粒子群算法中，每个粒子都有自己的位置($X$)和速度($v$)。在迭代过程中，更新每个粒子的速度和位置：$$v_i(t+1)=w\times v_i(t)+c_1\times r_1\times \left(X_{pbest}-X_i(t)\right)+c_2\times r_2\times (X_{gbest}-X_i(t))\text{\hspace{1em}(1)}$$$$X_i(t+1)=X_i(t)+v_i(t+1)\text{\hspace{1em}(2)}$$其中，$v$表示粒子的速度，$w$表示惯性权重，$X_{pbest}$表示粒子的个体最佳位置，$X$表示粒子的位置，$X_{gbest}$表示全局最佳位置，$c_1$和$c_2$为系数因子，$r_1$和$r_2$为随机数。
受粒子群算法的启发，本文设计了一种新的开发阶段速度引导的位置搜索公式，具体表达式如下：
在硬围攻策略中，位置由下式更新：$$v(t+1)=w\times v(t)+c_3\times r_3\times (X_{pbest}-X(t))+X_{rabbit}(t)+E\times \left|X_{rabbit}-X(t)\right|\text{\hspace{1em}(3)}$$$$X(t+1)=X(t)+v(t+1)\text{\hspace{1em}(4)}$$在软围攻策略中，位置由下式更新：$$v(t+1)=w\times v(t)+c_4\times r_4\times (X_{pbest}-X(t))+(X_{rabbit}-X(t))+E\times \left|J\times X_{rabbit}-X(t)\right|\text{\hspace{1em}(5)}$$$$X(t+1)=X(t)+v(t+1)\text{\hspace{1em}(6)}$$其中，$v$为每只鹰的速度，$X_{pbest}$为每只鹰的个体最佳位置，$c_3$和$c_4$为记忆因子，$r_3$和$r_4$为$[0,1]$中的随机数，$w$为惯性权重，由下式计算：$$w(t)=w_{\text{initial}}-(w_{\text{initial}}-w_{\text{end}})\times \left|\frac{t}{1+\sqrt{1+t^2}}\right|\text{\hspace{1em}(7)}$$其中，$w_{\text{initial}}$和$w_{\text{end}}$分别为$w$的初值和终值。
该策略有3个特点：
（1）增加速度项，增强位置搜索的全局搜索能力；
（2）鹰不仅从自己的信息中学习，还从种群中其他鹰的信息中学习；
（3）引入惯性权重$w$，动态平衡HHO的优化性能。

（2）非线性逃逸能量参数

与以往提出的$E$的非线性减小策略不同，本文提出了一种新的逃逸能量参数$E$的非线性增大方案，原因如下：一方面，鹰的种群在迭代搜索的早期具有较好的多样性；良好的多样性意味着$HHO$具有强大的探索整个搜索空间的能力。这一阶段的主要目标是加速收敛(即$E<1$)。另一方面，在迭代搜索的后期，HHO可能会在搜索空间的某个点上收敛，这将导致种群多样性的丧失。该阶段(即$E\ge 1$)的主要目的是保持种群多样性，避免局部最优。因此，所提参数$E$的计算公式为：$$E(t)=E_{\max }-(E_{\max }-E_{\min })\cdot \cos \left(\frac{t}{t_{\max }}\times \frac{\pi }{2}\right)\text{\hspace{1em}(8)}$$其中$E_{\max }$和$E_{\min }$分别为$E$的最大值和最小值。
从式(8)可以得出，所提出的非线性逃逸能量参数$E$在迭代前期和中期的数值较小($E<1$)，说明与全局探索阶段相比，该参数较长时间集中在局部开发阶段(约占总迭代数的67%)。本文提出的非线性逃逸能量参数$E$在后期较大，仅在33%左右的迭代中集中于探索。

（3）折射反向学习策略

具体原理请参考这里。执行过程如图1所示。

图1 折射反向学习策略流程

（4）VGHHO算法流程

融合以上3种策略提出的VGHHO算法的执行流程图如图2所示。

图2 VGHHO算法流程图

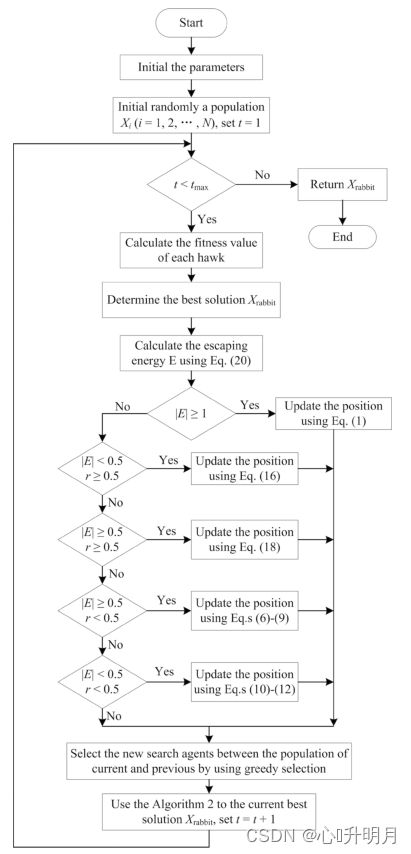
二、仿真实验与结果分析

将VGHHO与BOA、HHO、SCA、GWO和SSA进行对比，以文献[1]中表1的F1、F6、F8(单峰函数/30维)、F10、F13、F18(多峰函数/30维)为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

函数：F1
BOA：最差值: 8.7074e-11, 最优值: 6.1757e-11, 平均值: 7.7261e-11, 标准差: 5.9527e-12, 秩和检验: 1.2118e-12
HHO：最差值: 1.1413e-90, 最优值: 2.925e-112, 平均值: 3.8445e-92, 标准差: 2.0831e-91, 秩和检验: 1.2118e-12
SCA：最差值: 87.8156, 最优值: 0.003647, 平均值: 9.6636, 标准差: 20.4356, 秩和检验: 1.2118e-12
GWO：最差值: 8.0169e-27, 最优值: 2.0466e-29, 平均值: 1.1797e-27, 标准差: 1.6876e-27, 秩和检验: 1.2118e-12
SSA：最差值: 2.1989e-06, 最优值: 2.3833e-08, 平均值: 2.5419e-07, 标准差: 4.2315e-07, 秩和检验: 1.2118e-12
VGHHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F6
BOA：最差值: 8.38e-11, 最优值: 6.1137e-11, 平均值: 6.814e-11, 标准差: 5.1676e-12, 秩和检验: 1.2118e-12
HHO：最差值: 3.132e-95, 最优值: 1.2621e-115, 平均值: 1.2207e-96, 标准差: 5.7433e-96, 秩和检验: 1.2118e-12
SCA：最差值: 51.4736, 最优值: 0.00070649, 平均值: 2.8006, 标准差: 9.4694, 秩和检验: 1.2118e-12
GWO：最差值: 8.2647e-28, 最优值: 5.7949e-30, 平均值: 1.2943e-28, 标准差: 1.5238e-28, 秩和检验: 1.2118e-12
SSA：最差值: 10.5258, 最优值: 0.049281, 平均值: 1.8377, 标准差: 2.1058, 秩和检验: 1.2118e-12
VGHHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F8
BOA：最差值: 7.9527e-11, 最优值: 5.0019e-11, 平均值: 6.5226e-11, 标准差: 7.9895e-12, 秩和检验: 1.2118e-12
HHO：最差值: 7.1174e-87, 最优值: 2.3134e-107, 平均值: 2.373e-88, 标准差: 1.2994e-87, 秩和检验: 1.2118e-12
SCA：最差值: 9754.8256, 最优值: 4.7054, 平均值: 1436.5588, 标准差: 2158.5268, 秩和检验: 1.2118e-12
GWO：最差值: 6.1218e-23, 最优值: 5.8953e-26, 平均值: 4.41e-24, 标准差: 1.1125e-23, 秩和检验: 1.2118e-12
SSA：最差值: 32320853.9148, 最优值: 2412230.0348, 平均值: 11185842.4919, 标准差: 6845128.8024, 秩和检验: 1.2118e-12
VGHHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
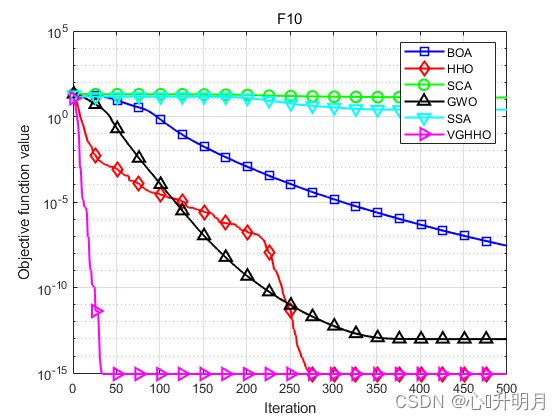
函数：F10
BOA：最差值: 3.554e-08, 最优值: 1.5905e-08, 平均值: 2.795e-08, 标准差: 4.8054e-09, 秩和检验: 1.2118e-12
HHO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
SCA：最差值: 20.3275, 最优值: 0.041294, 平均值: 12.9629, 标准差: 8.8587, 秩和检验: 1.2118e-12
GWO：最差值: 1.4655e-13, 最优值: 7.5495e-14, 平均值: 9.764e-14, 标准差: 1.6992e-14, 秩和检验: 1.1064e-12
SSA：最差值: 4.122, 最优值: 1.3404, 平均值: 2.5117, 标准差: 0.63971, 秩和检验: 1.2118e-12
VGHHO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
函数：F13
BOA：最差值: 8.6836e-11, 最优值: 2.6116e-18, 平均值: 7.9614e-12, 标准差: 2.0354e-11, 秩和检验: 1.2118e-12
HHO：最差值: 9.1833e-90, 最优值: 1.424e-115, 平均值: 3.0611e-91, 标准差: 1.6766e-90, 秩和检验: 1.2118e-12
SCA：最差值: 26.9776, 最优值: 0.4427, 平均值: 6.8765, 标准差: 5.6672, 秩和检验: 1.2118e-12
GWO：最差值: 9.7949e-21, 最优值: 3.8654e-28, 平均值: 3.2806e-22, 标准差: 1.788e-21, 秩和检验: 1.2118e-12
SSA：最差值: 124.5401, 最优值: 26.8674, 平均值: 66.6608, 标准差: 23.8924, 秩和检验: 1.2118e-12
VGHHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F18
BOA：最差值: 6.1343e-10, 最优值: 1.858e-11, 平均值: 2.9567e-10, 标准差: 1.6403e-10, 秩和检验: 1.2118e-12
HHO：最差值: 9.5378e-271, 最优值: 0, 平均值: 3.1793e-272, 标准差: 0, 秩和检验: 8.8658e-07
SCA：最差值: 0.0070985, 最优值: 2.0696e-07, 平均值: 0.00067805, 标准差: 0.0014976, 秩和检验: 1.2118e-12
GWO：最差值: 3.0254e-62, 最优值: 1.7843e-72, 平均值: 1.0302e-63, 标准差: 5.52e-63, 秩和检验: 1.2118e-12
SSA：最差值: 3.5642e-07, 最优值: 3.7009e-15, 平均值: 3.8616e-08, 标准差: 9.6042e-08, 秩和检验: 1.2118e-12
VGHHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN

实验结果表明：在大多数经典基准函数上，VGHHO算法比其他算法具有更高的精度和更好的可扩展性。

三、参考文献

[1] Long, W., Jiao, J., Liang, X. et al. A velocity-guided Harris hawks optimizer for function optimization and fault diagnosis of wind turbine[J]. Artificial Intelligence Review, 2022.