4、0-1背包问题
背包问题
对于0-1背包问题,由于我们对一个商品只有两种选择:要或者不要。于是我们的背包问题不是一个贪心算法问题,很简单
如果选用贪心算法,我们肯定是决定选用“商品单位重量价值最高“,如下面的例子则相反了
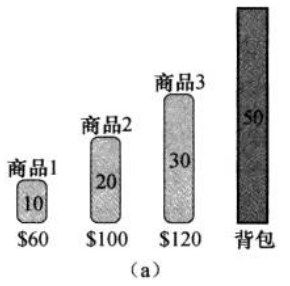
如上图中有3种商品的价值以及重量,背包容量为50.
那么如果选用贪心算法,则商品1的单位重量价值最高为60/10=6.
而商品2和商品3的分别为100/20和120/30为5和4.肯定不行,但是如果选用商品1,则2和3只能选一个
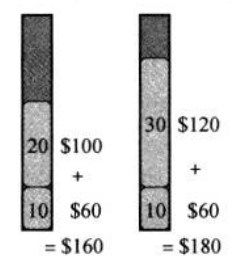
但是如果选用商品2和3,则:

于是,我们可以看到,选2和3的总价值高于选用1和其它的组合。
这是因为你选商品1和其它的组合后总是会浪费背包的一些空间,而商品2和3的组合却能够充分利用背包的容量。
结论:0-1背包问题是一个动态规划问题,而不是贪心算法问题。
主体函数代码如下:
void packageProb(int packageCap,int valueSum,int *productWeight,int *productValue,int *flag,int Len){ int i; std::cout<<valueSum<<std::endl; for(i=0;i<Len; i++){ int flag_f[3]={0}; int packageC=packageCap; int valueS=valueSum; for(int j=0;j<3; j++){ flag_f[j]=flag[j]; } if(packageC>=productWeight[i]&&!flag[i]){ int packageCC=packageCap-productWeight[i]; int valueSS=valueS+productValue[i]; flag_f[i]=1; for(int i=0;i<Len; i++){ if(flag_f[i]) std::cout<<i<<std::endl; } std::cout<<valueSS<<std::endl; std::cout<<std::endl; packageProb(packageCC,valueSS,productWeight,productValue,flag_f,Len); } }}
测试代码如下:
int productWeight[3]={10,20,30}; int productValue[3]={60,100,120}; int flag[3]={0}; packageProb(50,0,productWeight,productValue,flag,3);
如上面代码所以,对于递归问题,我们一定要知道每次向下递归的时候,程序的栈只会保存一些函数的局部变量和返回地址空间等信息,
不会保存调用参数中的值,调用参数是会在每次递归中是会跟着变的。