前面两篇文章我们了解了卡尔曼滤波以及扩展卡尔曼滤波在目标追踪的应用,我们在上一篇文章中还具体用Python实现了EKF,但是细心的同学会发现,EKF的效率确实很低,计算雅可比矩阵确实是一个很费时的操作,当问题(非线性的)一旦变得复杂,其计算量就变得十分不可控制。在此再向大家接受一种滤波——无损卡尔曼滤波(Unscented Kalman Filter, UKF)
创作不易,转载请注明来源:http://blog.csdn.net/adamshan/article/details/78359048
通过上一篇文章,我们已经知道KF不适用于非线性系统,为了处理非线性系统,我们通过一阶泰勒展式来近似(用线性函数近似),这个方案直接的结果就是,我们对于具体的问题都要求解对应的一阶偏导(雅可比矩阵),求解雅可比矩阵本身就是费时的计
激光雷达目标检测 (上)
**---- 转载自美团无人专送团队**
- 1
简介
安全性是自动驾驶中人们最关注的问题之一。
在算法层面,无人车对周围环境的准确感知是保证安全的基础,因此感知算法的精度十分重要。现有感知算法的思路一般通过某种数学模型对现实世界的某个子集进行拟合。
当情况足够简单的时候,算法可以得到较高的精度。例如现在很多无人驾驶公司有在限定的时间段和限定的场地内,用单一传感器的算法就可以得到非常高的精度。
但是自动驾驶中的实际问题非常复杂,各种天气、路况和障碍物的组合非常多,基于单一传感器的算法很难解决所有情况。例如在进隧道和出隧道时因为光线的突然变化摄像头会有欠曝光和过曝光问题,此时拍到的图片几乎全黑或全白,仅基于摄像头的感知算法很难在这种情况给出高精度的结果。
为了解决这种开放环境中的自动驾驶问题,很多自动驾驶公司提出了多传感器方案,希望通过取长补短来提高自动驾驶系统处理复杂环境的能力。现在最普遍使用的传感器是摄像头,除此之外还有激光雷达、毫米波雷达、GPS/IMU等。
激光雷达作为自动驾驶领域中最重要的传感器之一,常用于物体检测、道路分割和高精度地图构建。
本文主要讨论基于激光雷达的物体检测算法。在讨论具体的算法之前,首先要了解激光雷达数据的特点。
激光雷达原理和数据特点
现在自动驾驶中常用的激光雷达为机械式激光雷达,其由若干组可以旋转的激光发射器和接收器组成。每个发射器发射的一条激光束俗称“线“,主要有单线、4线、16线、32线、64线和128线雷达。
常见机械式激光雷达中激光束是波长在900nm左右的近红外光(NIR),可以根据激光直接获得周围一圈的准确的三维空间信息。
这种雷达的成像原理比较简单:发射器和接收器连接在一个可以旋转的机械结构上,某时刻发射器将激光发射出去,之后接收器接收返回的激光并计算激光与物体碰撞点到雷达原点的距离。
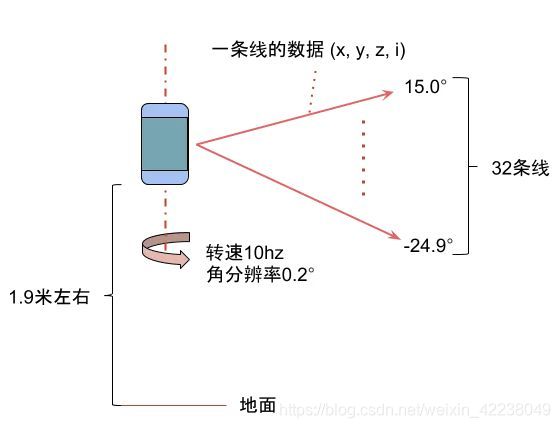
由于每次发射/接收的角度是预先设定的,因此根据距离、水平角度和垂直角度就能求出碰撞点相对于激光雷达中心的坐标。每条线每次发射激光得到的数据由一个四元组(x,y,z,i)表示,其中(x,y,z)是三维坐标,i表示反射强度。
图1:一个32线激光雷达的成像原理示意图
- 1
以某款32线激光雷达为例,32根线从上到下排列覆盖15.0°到-24.9°。
工作状态时这32根线在水平平面旋转可以采集一周360°的数据。雷达的旋转速度和角分辨率是可以调节的,常用速度为10hz(100ms转一圈)对应每0.2°采集一次数据,即角分辨率为360/0.2=1800。
由于光速非常快所以在1800中任何一个位置进行一次发射和接收动作可以看作是瞬时完成的。受到硬件能力的限制,一般转速越快则发射和接收激光的次数越少,即角分辨率越小。常用雷达采集到的数据点距离雷达中心一般不会超过150米。
通常采集到的360°的数据被称为一帧,上面的例子中一帧数据在理论上最多包含32*(360/0.2)=57600个点。
在实际情况中如果雷达被放置在车的上方大约距地面1.9米的位置,则在比较空旷的场景中大约获得40000个点,一部分激光点因为被发射向天空或被吸收等并没有返回到接收器,也就无法得到对应的点。下图是典型的一帧数据的可视化图。
图2:一个32线激光雷达的一帧数据的三维可视化图
- 1
激光雷达具有不受光照影响和直接获得准确三维信息的特点,因此常被用于弥补摄像头传感器的不足。激光雷达采集到的三维数据通常被称为点云,激光点云数据有很多独特的地方:
距离中心点越远的地方越稀疏;
机械激光雷达的帧率比较低,一般可选5hz、10hz和20hz,但是因为高帧率对应低角分辨率,所以在权衡了采样频率和角分辨率之后常用10hz;
点与点之间根据成像原理有内在联系,比如平坦地面上的一圈点是由同一个发射器旋转一周生成的;
激光雷达生成的数据中只保证点云与激光原点之间没有障碍物以及每个点云的位置有障碍物,除此之外的区域不确定是否存在障碍物;
由于自然中激光比较少见所以激光雷达生成的数据一般不会出现噪声点,但是其他激光雷达可能会对其造成影响,另外落叶、雨雪、沙尘、雾霾也会产生噪声点;
与激光雷达有相对运动的物体的点云会出现偏移,例如采集一圈激光点云的耗时为100ms,在这一段时间如果物体相对激光有运动,则采集到的物体上的点会被压缩或拉伸。
激光雷达物体检测算法
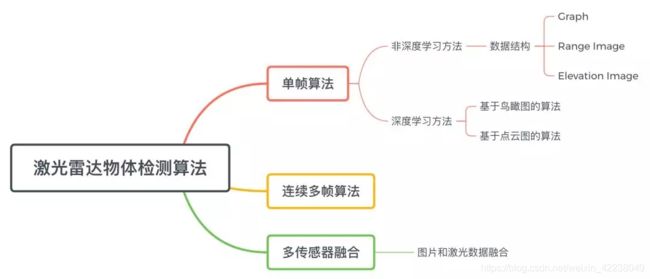
图3:本节的叙事结构
- 1
在深度学习流行之前主要用传统的机器学习方法对点云进行分类和检测。
在这个领域对于这些学习方法本身的研究并不多,研究者更倾向于直接把理论上较为成熟的方法应用到激光点云数据中。研究者将研究重点主要放在对数据本身特性的理解上,从而设计出适合点云的算法流程。
上一节点云图中最明显的规律是地面上的“环”,根据点云的成像原理当激光雷达平放在地面上方时,与地面夹角为负角度的“线”在地面上会形成一圈一圈的环状结构。
因为这种结构有很强的规律性所以很多物体检测算法的思路是先做地面分割然后做聚类,最后将聚类得到的物体进行识别。为了提高算法的速度,很多算法并不直接作用于三维点云数据,而是先将点云数据映射到二维平面中然后再处理。常见的二维数据形式的有Range Image和Elevation Image。
从2014年开始深度学习广泛地被应用在各个领域,随着图片物体检测算法的发展,点云物体检测也逐步转向了深度学习。
现在自动驾驶中一般关注鸟瞰图中物体检测的效果,主要原因是直接在三维中做物体检测的精确度不够高,而且目前来说路径规划和车辆控制一般也只考虑在二维平面中车体的运动。
现在在鸟瞰图中的目标检测方法以图片目标检测的方法为主,主要在鸟瞰图结构的建立、物体的空间位置的估计以及物体在二维平面内的旋转角度的估计方面有所不同。
从检测结果来看这类算法比在三维空间中的物体检测要好。直接作用在三维空间中的物体检测方法在近年来也有所突破,其通过某种算子提取三维点云中具有点云顺序不变性的特征,然后通过特殊设计的网络结构在三维点云上直接做分类或分割。
这类方法的优点是能对整个三维空间任何方向任何位置的物体进行无差别的检测,其思路新颖但是受限于算法本身的能力、硬件设备的能力以及实际应用的场景,现在还不能在实际中广泛地使用。
自动驾驶对于检测算法有着比较特殊的要求:首先为了安全性考虑召回率要高,即不能漏检;其次因为检测到的物体是下游路径规划和运动决策算法的输入,这要求检测到的目标在连续帧中具有较好的稳定性,具体而言即在连续帧中检测到的同一个物体的类别、尺寸、位置和方向不能有剧烈的变化。与此同时因为激光点云的稀疏性,现有算法单用一帧点云数据无法在小物体、远处物体和被遮挡物体的检测上得到令人满意的结果。
因此近几年人们开始考虑结合多种传感器数据的方法、结合多个激光雷达的方法以及结合连续多帧的方法。
虽然在学术界的排行榜中现在最好的方法是基于深度学习的算法,但是在实际问题中数据的预处理、后处理等对最终结果有着至关重要的影响,而这些部分的算法往往需要根据数据和使用场景有针对性的设计。
所以本节首先会介绍一些单帧目标检测中的非深度学习算法中对于激光数据的处理方式,然后会在下集介绍深度学习算法以及多帧目标检测算法中介绍几个具有代表性的方法。
非深度学习算法
2015年之前应用在激光雷达领域的检测和分类模型以线性模型、SVM和决策树为主。这些模型的泛化能力和复杂程度无法在实际场景中满足人们的需求,因此研究者将注意力更多的放在了对于点云数据特性的挖掘上。常见的算法流程为:
将三维点云映射为某种结构,例如Graph和Range Image;
提取每个节点或像素的特征;
将节点或像素聚类;
通过一定规则或分类器将一个或多个聚类确定为地面;
结合地面信息,通过分类器对其他聚类进行物体级别的识别;
把所有的检测、识别的结果映射回三维点云中。
从检测和分类的效果来说,这类方法远没有基于深度学习的方法好。
但无论是基于Graph或是基于Range Image的结构都比单纯的点云蕴涵了更多的信息。在这些结构中有时使用简单的基于规则的方法就可以得到比较好的结果,这一点在实际应用中非常重要。例如在物体检测任务中出现了训练集合中未出现过的物体,基于学习的方法一般无法正确地将其检测出来。但是基于简单规则的方法却可以正常给出检测结果,虽然此时分类结果往往是未知。
在自动驾驶中检测算法的漏检问题远比错分类问题严重很多,从这个角度说基于简单规则的方法是保证安全的一把锁。从实时数据预处理的效率来说,在实际环境中为了提高检测精度需要将离散的噪声点和不在检测范围内的物体过滤掉。在Graph和Range Image中进行噪声数据的过滤有时比直接在点云上做效率高。
1 基于Graph的方法
基于Graph的建模方法指直接根据三维点云直接建立无向图G = {N, E},N表示图中的节点E表示节点之间的边。常用的建图方式是将三维点云中每个点的坐标(x,y,z)作为一个节点。找到每个节点对应的雷达的线数l和水平方向的旋转角度θ,当两个节点i和j满足下面任何一个条件时为这两个节点建立一条边。即如果两个点由相邻线在同一时刻产生,或由同一根线在相邻时刻产生,则为两个点建立一条边。数学描述如下:
|l_i - l_j| = 1 and θ_i = θ_j
l_i = l_j and (θ_i - θ_j) mod 360 = r
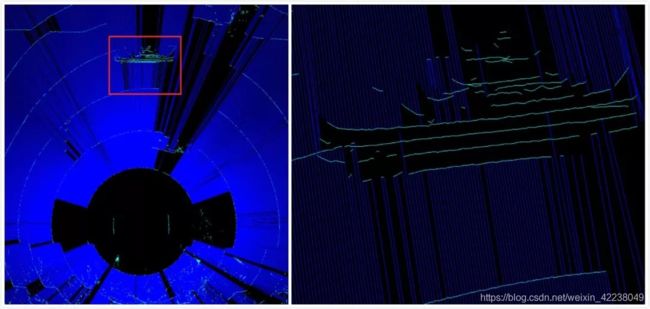
这里r表示水平方向的最小旋转角,上节例子中r=0.2。实际在建图时会增加其他约束,比如两个节点的距离不能太远或两个节点的高度差不能太大等。上节中点云的建图结果可视化如下图,深蓝色表示满足第一个条件的边,浅蓝色表示满足第二个条件的边。
图4:在激光点云中直接根据三维点云信息建立Graph的可视化结果,其中深蓝色的是纵向的边,浅蓝色的是横向的边。右侧的图是左侧的局部放大版本。
- 1
建图的目的是在空间中离散的三维点之间建立某种联系,从而为后续的聚类和分割做准备。一般这种建图的方法不设定边的权重,依靠节点的特征进行聚类和分割。
Moosmann提出了一种使用法向量作为节点特征的方法【1】。其思路是将点云看成连续曲面上的离散采样。所谓法向量是指曲面在每个节点处的法向量,如果两个相邻的节点的法向量相似则说明这两个节点所在局部平面比较光滑,那么这两个节点应当属于一个同一个物体。论文中使用一种简单快速的方法对于每个节点位置的法向量进行估计,即首先计算所有相邻平面的法向量(如下图蓝色箭头),然后求法向量的几何平均值并进行归一化(下图红色箭头),最后所有节点的法向量再根据所有相邻节点进行均值滤波。
图5:节点法向量的可视化例子。红色和蓝色的圆形是节点,蓝色的箭头描述了每三个相邻点组成的平面的法向量,红色的箭头描述了最终得到的法向量。
- 1
得到特征之后就可以根据相邻节点之间的特征相似性进行聚类,聚类的首要目的一般是求出属于地面的节点即地面分割。
Douillard为不同的数据类型提出了不同的地面分割方法【2】。其基于Graph结构的地面分割算法的核心思想是:首先确定属于地面的种子节点然后由内向外进行区域增长。
论文中提出的算法为了在处理各种边缘情况的同时尽可能的增加地面节点的召回率,手工设定了一系列复杂的约束条件。这样做确实在实验指标上看起来好一些,但是在实际的应用中关注更多的并不是地面节点的召回,而是地面节点在所有可行驶区域内的分布是否均匀。一般来说根据这个目标在实际场景中只用很简单的决策树,就可以建立出满足应用要求的约束模型。Douillard在得到地面之后通过聚类算法找到其他类别的物体如下图。
图6:基于传统方法的物体检测的可视化结果
- 1
上面介绍的建图的方法只能作用在低速单帧的数据中。因为在高速情况由于多普勒效应很难准确为每一个三维点找到其对应的雷达线数和水平旋转角度,多帧的情况也类似。而更通用的建模方法是为每个节点寻找最邻近的k的节点建立边。这种方法虽然可以建立八叉树等数据结构进行加速,但是没有在Range Image中建图的效率高。
2 基于Range Image的方法
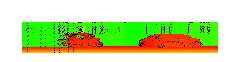
Range Image是指距离图,即一种类似图片的数据结构。以上节32线激光雷达的数据为例子,对应的Range Image宽360/0.2=1800像素,高32像素。每个像素值表示对应点到原点的距离。上节中的点云对应的Range Image的的可视化如下图,因为这个图非常细长所以只截取了一小段。黑色的部分缺少对应的点云信息,其他的不同颜色代表不同距离。
图7:一个Range Image的例子。
- 1
Zhu提出了一种在Range Image中建立无向图G = {N, E}的方法【3】。即在图中每一个像素代表一个节点,以每一个节点为中心在二维平面上以一定距离搜索其他节点,如果两个节点在三维空间中满足某些条件则建立一条边,边的权重是两个点在三维空间中的距离。建图之后使用基于图的分割算法(例如【4】)即可得到聚类结果。
这种方法建图的速度非常快,在实际使用过程中还需要处理多个点映射到同一个像素的情况,其建图的结果和直接在三维点云中建图相比非常接近。Range Image不仅仅能为计算进行提速,还可以做到一些不方便在点云上直接处理的事情,因为其比点云包含了更多的信息。
Biasutti提出了一种对点云中被遮挡的部分进行还原的方法【5】。其思路是:首先将点云生成Range Image结构并在其中进行聚类,然后选择某个物体所代表的类并在图中抹掉,之后根据周围像素将抹掉的部分复原出来,最后将Range Image映射回点云。下图是论文中的算法的结果,可以看出白色的行人被抹掉了,而地面上的空洞被漂亮的填充了。
图8:被遮挡点云和还原被遮挡点云的对比图,左图是原始点云,右侧是将人去掉后的点云。
- 1
UKF使用的是统计线性化技术,我们把这种线性化的方法叫做无损变换(unscented transformation)这一技术主要通过n个在先验分布中采集的点(我们把它们叫sigma points)的线性回归来线性化随机变量的非线性函数,由于我们考虑的是随机变量的扩展,所以这种线性化要比泰勒级数线性化(EKF所使用的策略)更准确。和EKF一样,UKF也主要分为预测和更新。
运动模型
本篇我们继续使用CTRV运动模型,不了解该模型的同学可以去看上一篇博客,CTRV模型的具体形式如下: