基于蚁群算法的函数寻优算法
文章目录
- 一、理论基础
- 二、案例背景
-
- 1、问题描述
- 2、解题思路及步骤
- 三、MATLAB程序实现
-
- 1、清空环境变量
- 2、初始化参数
- 3、构建解空间和目标函数
- 4、迭代寻优
- 5、结果显示
- 6、绘图
- 四、参考文献
一、理论基础
请参考这里
二、案例背景
1、问题描述
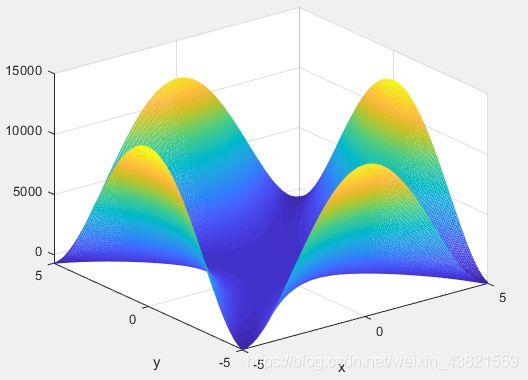
本案例的寻优函数为: f ( x , y ) = 20 ( x 2 − y 2 ) 2 − ( 1 − y 2 ) 2 − 3 ( 1 + y ) 2 + 0.3 , x ∈ [ − 5 , 5 ] , y ∈ [ − 5 , 5 ] f(x,y)=20(x^2-y^2)^2-(1-y^2)^2-3(1+y)^2+0.3,\quad x∈[-5,5],y∈[-5,5] f(x,y)=20(x2−y2)2−(1−y2)2−3(1+y)2+0.3,x∈[−5,5],y∈[−5,5]函数图形如图1所示。
2、解题思路及步骤
(1)初始化蚂蚁个数 m = 300 m=300 m=300,最大迭代次数 i t e r _ m a x = 80 iter\_max=80 iter_max=80,信息素挥发因子 R h o = 0.9 Rho=0.9 Rho=0.9,转移概率常数 P 0 = 0.2 P_0=0.2 P0=0.2,局部搜索步长 s t e p = 0.05 step=0.05 step=0.05。
(2)随机产生蚂蚁初始位置,计算适应度函数值,设为初始信息素,计算状态转移概率,其计算公式为 P ( i t e r , i ) = m a x ( T a u ) − T a u ( i ) m a x ( T a u ) (1) P(iter, i) = \frac{max(Tau)-Tau(i)}{max(Tau)} \tag{1} P(iter,i)=max(Tau)max(Tau)−Tau(i)(1)其中, m a x ( T a u ) max(Tau) max(Tau)表示信息素的最大值, T a u ( i ) Tau(i) Tau(i)表示蚂蚁 i i i的信息素, P ( i t e r , i ) P(iter, i) P(iter,i)表示第 i t e r iter iter次迭代蚂蚁 i i i的转移概率值。
(3)进行位置更新:当状态转移概率小于转移概率常数时,进行局部搜索,其搜索公式为 n e w = o l d + r 1 ⋅ s t e p ⋅ λ (2) new=old+r_1·step·\lambda \tag{2} new=old+r1⋅step⋅λ(2)其中, n e w new new为待移动的位置, o l d old old为蚂蚁当前位置, r 1 r_1 r1为介于[-1,1]的随机数, s t e p step step为局部搜索步长, λ \lambda λ为当前迭代次数的倒数;当状态转移概率大于转移概率常数时,进行全局搜索,其搜索公式为 n e w = o l d + r 2 ⋅ r a n g e (3) new=old+r_2·range\tag{3} new=old+r2⋅range(3)其中, r 2 r_2 r2为[-0.5,0.5]的随机数, r a n g e range range为自变量的区间大小。
通过判断待移动位置的函数值与当前位置函数值的大小来确定是否更新蚂蚁当前的位置,并利用边界吸收方式进行边界条件处理,将蚂蚁位置界定在取值范围内。
(4)计算新的蚂蚁位置的适应度值,判断蚂蚁是否移动,更新信息素,信息素更新公式为 T a u = ( 1 − R h o ) ⋅ T a u + f (4) Tau = (1 - Rho) \boldsymbol·Tau + f\tag{4} Tau=(1−Rho)⋅Tau+f(4)其中, R h o Rho Rho为信息素挥发因子, T a u Tau Tau为信息素, f f f为目标函数值。
(5)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
三、MATLAB程序实现
利用MATLAB提供的函数,可以方便地在MATLAB环境下实现上述步骤。
1、清空环境变量
程序运行之前,清除工作空间Workspace中的变量及Command Window中的命令。具体程序如下:
%% 清空环境变量
clear all
clc
2、初始化参数
在计算之前,需要对参数进行初始化。同时,为了加快程序的执行速度,对于程序中涉及的一些过程变量,需要预分配其存储容量。具体程序如下:
%% 初始化参数
m = 300; % 蚂蚁数量
iter_max = 80; % 最大迭代次数
Rho = 0.9; % 信息素挥发因子
P0 = 0.2; % 转移概率常数
step = 0.05; % 局部搜索步长
Tau = zeros(m, 1); % 信息素矩阵
P = zeros(iter_max, m); % 转移概率矩阵
trace = zeros(iter_max, 1); % 每代最优值
x_lower = -5; % x范围下限
y_lower = -5; % y范围下限
x_upper = 5; % x范围上限
y_upper = 5; % y范围上限
3、构建解空间和目标函数
构建解空间代码如下:
%% 构建解空间
ant = zeros(m, 2); % 随机生成蚁群位置
for i = 1: m
ant(i, 1) = x_lower + (x_upper - x_lower) * rand;
ant(i, 2) = y_lower + (y_upper - y_lower) * rand;
Tau(i) = fun(ant(i, 1), ant(i, 2)); % 信息素
end
%% 绘图显示
[x, y] = meshgrid(x_lower:0.05:x_upper, y_lower:0.05:y_upper);
f = '20*(x.^2-y.^2).^2-(1-y.^2).^2-3*(1+y).^2+0.3';
z = eval(f);
figure(1);
mesh(x, y ,z)
hold on;
plot3(ant(:, 1), ant(:, 2), Tau, 'k*');
xlabel 'x'; ylabel 'y'; zlabel 'z';
title '蚁群初始位置';
目标函数代码如下:
function z = fun(x, y)
z = 20*(x.^2-y.^2).^2-(1-y.^2).^2-3*(1+y).^2+0.3;
4、迭代寻优
迭代寻优为整个算法的核心。首先计算状态转移概率;然后根据转移概率的值判断哪些蚂蚁需要进行局部搜索,哪些蚂蚁需要进行全局搜索,之后再进行搜索,搜索完了之后一定要进行边界处理,并更新蚂蚁的位置;最后,更新信息素,每次迭代保存最优解。
%% 迭代寻优
for iter = 1:iter_max
lamda = 1 / iter;
[Tau_best, BestIndex] = max(Tau);
%% 计算状态转移概率
for i = 1:m
P(iter, i) = (Tau_best - Tau(i)) / Tau_best;
end
%% 位置更新
for i = 1:m
%% 局部搜索
if P(iter, i) < P0
temp1 = ant(i, 1) + (2 * rand - 1) * step * lamda;
temp2 = ant(i, 2) + (2 * rand - 1) * step * lamda;
else
%% 全局搜索
temp1 = ant(i, 1) + (x_upper-x_lower)*(rand-0.5);
temp2 = ant(i, 2) + (y_upper-y_lower)*(rand-0.5);
end
%% 边界处理
if temp1 < x_lower
temp1 = x_lower;
elseif temp1 > x_upper
temp1 = x_upper;
end
if temp2 < y_lower
temp2 = y_lower;
elseif temp2 > y_upper
temp2 = y_upper;
end
%% 判断蚂蚁是否移动
if fun(temp1, temp2) > fun(ant(i, 1), ant(i, 2))
ant(i, 1) = temp1;
ant(i, 2) = temp2;
end
end
%% 迭代过程中蚂蚁移动图
figure(2);
mesh(x, y ,z);
hold on;
plot3(ant(:, 1), ant(:, 2), fun(ant(:, 1), ant(:, 2)), '*', 'color', [iter/iter_max, 0, 0]);
hold off;
xlabel 'x'; ylabel 'y';
title '蚁群算法迭代过程中蚂蚁移动';
pause(0.1)
frame = getframe(gcf);
imind = frame2im(frame);
[imind, cm] = rgb2ind(imind, 256);
if iter == 1
imwrite(imind, cm, 'test.gif', 'gif', 'Loopcount', inf, 'DelayTime', 1e-4);
else
imwrite(imind, cm, 'test.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 1e-4);
end
%% 更新信息素
for i = 1: m
Tau(i) = (1 - Rho) * Tau(i) + fun(ant(i, 1), ant(i, 2));
end
%% 保存最优解
[value, index] = max(Tau);
trace(iter) = fun(ant(index, 1), ant(index, 2));
end
迭代过程中蚂蚁的移动位置如图3所示。
5、结果显示
为了更为直观地对结果进行观察和分析,将寻找到的最优自变量及其最优函数值显示在Command Window中。具体程序如下:
%% 结果显示
[~, max_index] = max(Tau);
max_X = ant(max_index, 1);
max_Y = ant(max_index, 2);
max_value = fun(max_X, max_Y);
disp(['最优自变量:', num2str(ant(max_index, :))]);
disp(['最优函数值:', num2str(max_value)]);
由于各个蚂蚁的初始位置是随机生成的,因此每次运行的结果都会有所不同。某次运行的结果如下:
最优自变量:5 -0.0031313
最优函数值:12496.309
6、绘图
为了更为直观地对结果进行观察和分析,以图形的形式将结果显示出来,具体程序如下:
%% 绘图
figure;
mesh(x, y ,z);
hold on;
x = ant(:, 1);
y = ant(:, 2);
plot3(x, y ,eval(f), 'k*');
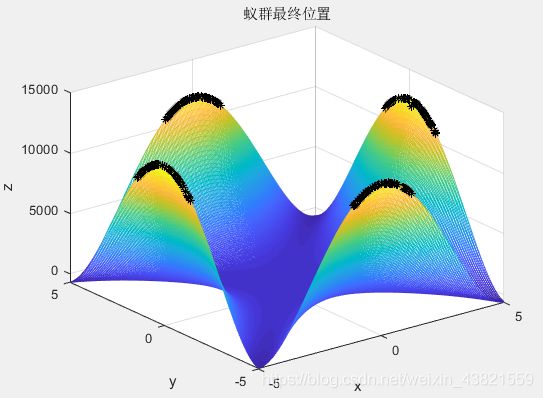
xlabel 'x'; ylabel 'y'; zlabel 'z';
title '蚁群最终位置';
figure;
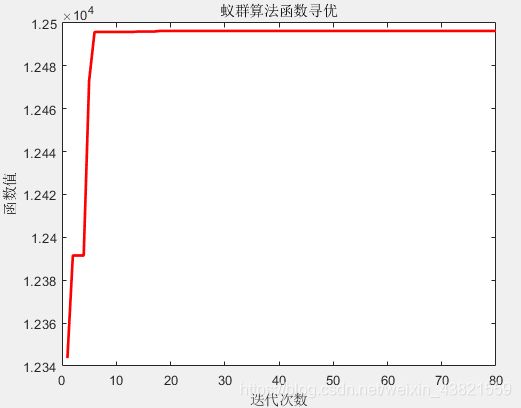
plot(1:iter_max, trace, 'r', 'LineWidth', 2);
title '蚁群算法函数寻优';
xlabel '迭代次数'; ylabel '函数值';
四、参考文献
[1] 心升明月. 基于蚁群算法的旅行商问题(TSP)的优化. CSDN博客.
[2] 凯旋16668. 【啃书】《智能优化算法及其MATLAB实例》例5.2蚁群算法进行函数寻优. CSDN博客.
[3] 曲怪曲怪. 《智能算法》专栏. CSDN博客.
[4] 郁磊, 史峰, 王辉, 等. MATLAB智能算法30个案例分析(第2版)[M]. 北京: 北京航空航天大学出版社, 2015.