动态规划
动态规划初步
动态规划是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间远远少于朴素解法。
对于一个初学者来说,空洞的理论远不如简单的实践来得直观有趣,因此还是从一道经典的DP问题出发吧,下面的题目取自HDU_2048:
Problem Description 在讲述DP算法的时候,一个经典的例子就是数塔问题,它是这样描述的:
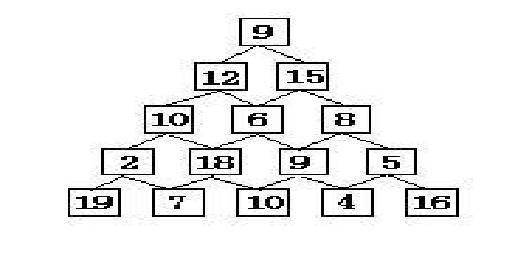
有如下所示的数塔,要求从顶层走到底层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
已经告诉你了,这是个DP的题目,你能AC吗?
Input
输入数据首先包括一个整数C,表示测试实例的个数,每个测试实例的第一行是一个整数N(1 <= N <= 100),表示数塔的高度,接下来用N行数字表示数塔,其中第i行有个i个整数,且所有的整数均在区间[0,99]内。
Output 对于每个测试实例,输出可能得到的最大和,每个实例的输出占一行。 Sample Input 1 5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 Sample Output 30
动态规划的关键步骤是找到问题的状态和状态转移方程。我们把当前位置(i, j)看成是一个状态,然后定义该状态下的指标函数d(i, j)为从第i 行的第j 个数字(包括它本身)到数塔底层的最佳路径的数字之和。在这个状态的定义下,原问题的解就是d(1, 1)。由于可以在向左走或向右走这两个决策中权衡,因此可以得到状态方程:d(i, j) = a[i, j] + max{d(i+1, j), d(i+1, j+1)},据此可以编写简单有效的递归方法:
#include<stdio.h> // 递归超时版,O(2^n).
#include<string.h>
#define MAXN 100
int a[MAXN+10][MAXN+10];
int height;
int dp(int, int);
int main(void)
{
int cases;
scanf("%d", &cases);
while(cases--)
{
scanf("%d", &height);
for(int low = 1; low <= height; low++)
for(int col = 1; col <= low; col++)
{
scanf("%d", &a[low][col]);
}
printf("%d\n", dp(1, 1));
}
return 0;
}
int dp(int i, int j)
{
if(i == height)
return a[i][j];
else
{
int x = dp(i+1, j);
int y = dp(i+1, j+1);
return a[i][j] + (x > y ? x : y);
}
}
正如注释上所写,这个程序提交到OJ评测结果超时,原因很简单,递归调用深度虽然不大(最大100次),但是调用次数太多了,其时间复杂度为O(2^n)。怎么解决这个问题呢?答案是:记忆化搜索。如下:
#include<stdio.h>
#include<string.h>
#define MAXN 100
int a[MAXN+10][MAXN+10];
int dp[MAXN+10][MAXN+10];
int height;
int f(int, int);
int main(void)
{
int cases;
scanf("%d", &cases);
while(cases--)
{
scanf("%d", &height);
memset(dp, -1, sizeof(dp)); // 从底层上来看,每个字节设为-1,导致数组最终的int型元素同样是-1。注意除0和-1外的其他的数值没有这个特性。
for(int low = 1; low <= height; low++)
for(int col = 1; col <= low; col++)
{
scanf("%d", &a[low][col]);
}
printf("%d\n", f(1, 1));
}
return 0;
}
int f(int i, int j) // 记忆搜索,O(n^2)
{
if(i == height)
return a[i][j];
else
{
if(dp[i+1][j] == -1)
dp[i+1][j] = f(i+1, j);
if(dp[i+1][j+1] == -1)
dp[i+1][j+1] = f(i+1, j+1);
return a[i][j] + (dp[i+1][j] > dp[i+1][j+1] ? dp[i+1][j] : dp[i+1][j+1]); // 注意三目运算符与双目运算符的优先级
}
}
可以看到,记忆化搜索的方式避免了对同一个子问题的重复求解,因此时间复杂度从原来的O(2^n)降到了O(n^2)。
其实,有了递推公式,我们可以用迭代的方式来求解问题,从而避免递归,递推公式的求解过程:从顶点出发时到底向左走还是向右走取决于是从左走能取到最大值还是从右走能取到最大值,只有左右两道路径上的最大值求出来了才能做出决策。同样地,下一层的走向又要取决于再下一层上的最大值是否已经求出才能做出决策。这样递推下去,最后一层作为边界条件,其本身的值就是最大值。所以,我们有递推公式,d(i, j) = a[i, j], i = n; d(i, j) = a[i, j] + max{d(i+1, j), d(i+1, j+1)}因此我们可以避开递归,从最后一行开始向上逐行递推,就能求得问题的解d(1, 1):
#include<stdio.h> //递推版
#include<string.h>
#define MAXN 100
int a[MAXN+10][MAXN+10];
int dp[MAXN+10][MAXN+10];
int main(void)
{
int cases, height;
scanf("%d", &cases);
while(cases--)
{
scanf("%d", &height);
memset(dp, 0, sizeof(dp));
for(int low = 1; low <= height; low++)
for(int col = 1; col <= low; col++)
{
scanf("%d", &a[low][col]);
}
for(int low = height; low >=1; low--) // dp数组的每一个结点都保存从底层到该结点的最大数字和
for(int col = 1; col <= low; col++)
{
dp[low][col] = a[low][col] + (dp[low+1][col] > dp[low+1][col+1] ? dp[low+1][col] : dp[low+1][col+1]); // 注意运算符优先级
}
printf("%d\n", dp[1][1]);
}
return 0;
}
最后,如果题目要求输出数字之和最大值的同时打印结点的值,也就是输出最佳路径上的每个数字怎么办?简单,如下面的程序所示,我们用一个二维数组left_right维护数值0和1。0代表当前节点向左走能取得最大值,1代表当前节点向右走能取得最大值。最后,只需要根据left_right数组的提示自顶向下访问原二维数组,顺便打印其节点上的数值即可。我们只对记忆化搜索的版本做出修改实现上述功能,递推版的做类似修改可以达到同样的效果。
// 打印路径
#include<stdio.h>
#include<string.h>
#define MAXN 100
int a[MAXN+10][MAXN+10];
int dp[MAXN+10][MAXN+10];
int left_right[MAXN+10][MAXN+10];
int height;
int f(int, int);
int main(void)
{
int cases;
scanf("%d", &cases);
while(cases--)
{
scanf("%d", &height);
memset(dp, -1, sizeof(dp)); // 从底层上来看,每个字节设为-1,导致数组最终的int型元素同样是-1。注意除0和-1外的其他的数值没有这个特性。
memset(left_right, 0, sizeof(left_right));
for(int low = 1; low <= height; low++)
for(int col = 1; col <= low; col++)
{
scanf("%d", &a[low][col]);
}
printf("%d\n", f(1, 1));
printf("path:\n");
printf("%d ", a[1][1]);
height--;
int i, j;
i = j = 1;
while(height--)
{
if(left_right[i][j] == 0)
printf("%d ", a[i+1][j]);
else
{
printf("%d ", a[i+1][j+1]);
j++;
}
i++;
}
printf("\n");
}
return 0;
}
int f(int i, int j) // 记忆搜索,O(n^2)
{
if(i == height)
return a[i][j];
else
{
if(dp[i+1][j] == -1)
dp[i+1][j] = f(i+1, j);
if(dp[i+1][j+1] == -1)
dp[i+1][j+1] = f(i+1, j+1);
if(dp[i+1][j] < dp[i+1][j+1])
left_right[i][j] = 1;
return a[i][j] + (dp[i+1][j] > dp[i+1][j+1] ? dp[i+1][j] : dp[i+1][j+1]);
}
}
All Rights Reserved. Author:海峰:) Copyright © xp_jiang. 转载请标明出处:http://www.cnblogs.com/xpjiang/p/4418024.html