西瓜书笔记之 模型评估与选择

讲真，这书是越看觉得自己不会的越多，感觉好多概念，完全不是理工男喜欢的样子。。

首先了解一下NP问题，机器学习面临的问题多是NP完全问题(NP-C问题)，号称世界七大数学难题之一。 NP的英文全称是Non-deterministic Polynomial Complete的问题，即多项式复杂程度的非确定性问题。怎么样，有没有被吓到。
看了百度百科对NP问题的解释，感觉营养还比较丰富，有兴趣可以看下NP
完全问题。为了解决各式各样NP问题，需要用到各种各样的算法，譬如：神经网络算法，遗传算法等等。对于某个具体问题，诸多算法，哪个好哪个坏，怎么评估，就是这章的主要内容。

一、留出法（hold-out）：

要对算法做评估是要依据数据的，将数据集一般分为训练集和测试集，一般将2/3至4/5的数据用于训练数据。 也有把数据集分为 训练集（80%）、验证集（10%）和测试集（10%）三部分，训练集建立模型，验证集优化模型，测试集测试模型。

二、交叉验证法（cross validation）

：把数据集分成k份,就是好多份，【留出法是分两份（训练集一份，测试集一份）】，这k份都是数据量相似的互斥子集，然后每次用k-1份作为训练集，剩余一份用作测试集。总共进行k次训练和测试，然后再返回k个测试结果的均值。 k最常用的值为10，其它常用值为5或20等。
下图给出10折交叉验证图：
这还没完，由于划分子集的方法不同，可以把同一数据集按照不同的分法，分为好多种，记为p次，然后评估结果是这p次k折交验结果的均值。
交叉检验法有一种特例叫留一法（leave one out,简称LOO),就是数据集有m个样本，我就把它分为m份数据，每个数据子集只包含一个样本，这样训练集就有m-1个数据，测试集只有一个样本数据。留一法的评估结果往往被认为比较准确，但也有计算复杂度等缺陷。

三、自助法（bootstrapping）

一个数据集D包含m个样本，咱们每次从数据集里随机选取一个，选取m次，得到的数据集合D‘，作为训练集，而没被选中的样本作为测试集。这样训练集就有和原始数据集同样数量的样本。
自助法在数据集小、难以有效划分训练/测试集时比较有用。数据量较多时，用留出法和交叉验证法更好。

穿插点小概念：

误差（error）：学习器的实际预测输出与样本的真实输出之间的差异称为“误差”，学习器在训练集上的误差称为“训练误差”（training error）或“经验误差”（empirical error）,在新样本上的误差称为“泛化误差”（generalization error）。

过拟合（overfitting）:过拟合是机器学习面临的关键障碍，各类学习算法都必然带一些针对过拟合的措施。我的理解，学到太过分了，不会举一反三了，就是过拟合。与过拟合对应的欠拟合（underfitting）就是学的太浅了。举个例子，当机器把驴当成马时，就是欠拟合，当机器觉得白马非马而是白马时，过拟合。

调参（parameter tuning）:在进行模型评估与选择时，除了要对适用学习算法进行选择，还需要对算法参数进行设定，这就是通常所说的调参。

验证集（validation set）:训练集的一个子集，在模型评估中用于评估测试的数据称为验证集。测试集用来评估泛化能力。验证集用来模型选择和调参。

性能度量（performance measure）: 对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量。
归一化（Normalization）：是将不同变化范围的值映射到相同的固定范围中，常见的有[0，1]。
通过留出法、交叉验证法和自助法得到了可以表现泛化误差的测试误差后，如何选出表现最佳的学习器呢？这就需要对泛化能力有一个评价标准。什么样的学习器是好的，不仅取决于算法和数据，还决定于任务需求。

四、性能度量

均方误差：

这公式写起来太复杂上图吧，还比较容易理解。f(x)就是学习预测值，与y(真实值）作差。然后把各样本的误差平方后求个平均值。

这个公式和上面那个公式意思雷同，积分了一下。

错误率：

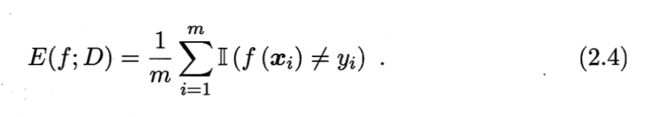
Ⅱ（f(x)≠y）返回1或者0，如果预测值f(x)不等于真实值y,那么就返回1。
与之对应的是精度。
精度：

查准率P(precision)与查全率R:(recall)

查准率：检索出来的信息有多少是用户感兴趣的。
P=TP/TP+FP
查全率：用户感兴趣的信息中有多少是被检索出来的。
R=TP/TP+FN
有了这两项才有了PR曲线：

简单一点比面积，复杂一下比平衡点（BEP break-even point），再复杂一下才有了F1度量。。。
这样够了吧。。不行。。还不够。还要来个加权调和平均。

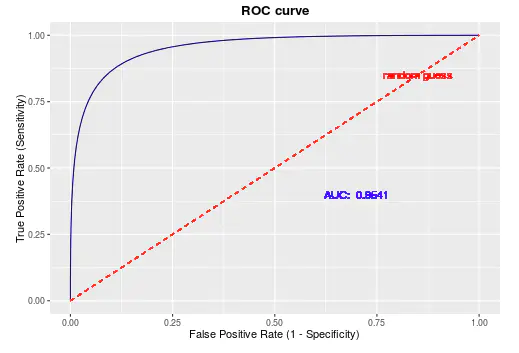
ROC曲线与AUC

ROC（Receiver Operating Characteristic）受试者工作特征，横轴：假正例率，纵轴：真正例率。为什么有了PR曲线，还要用ROC呢，ROC曲线有一个巨大的优势就是，当正负样本的分布发生变化时，其形状能够基本保持不变，而P-R曲线的形状一般会发生剧烈的变化，因此该评估指标能降低不同测试集带来的干扰，更加客观的衡量模型本身的性能，ROC曲线（AUC的值）会是一个更加稳定能反映模型好坏的指标。AUC:Area Under Roc Curve.
其主要的分析方法就是画这条特征曲线。ROC曲线起源于第二次世界大战时期雷达兵对雷达的信号判断【1】。当时每一个雷达兵的任务就是去解析雷达的信号，但是当时的雷达技术还没有那么先进，存在很多噪声（比如一只大鸟飞过），所以每当有信号出现在雷达屏幕上，雷达兵就需要对其进行破译。有的雷达兵比较谨慎，凡是有信号过来，他都会倾向于解析成是敌军轰炸机，有的雷达兵又比较神经大条，会倾向于解析成是飞鸟。这个时候，雷达兵的上司就很头大了，他急需一套评估指标来帮助他汇总每一个雷达兵的预测信息，以及来评估这台雷达的可靠性（如果不论哪一类雷达兵都能准确预测，那这台雷达就很NB～读者可思考其缘由）。于是，最早的ROC曲线分析方法就诞生了，用来作为评估雷达可靠性的指标～在那之后，ROC曲线就被广泛运用于医学以及机器学习领域～
举一个简单的例子方便大家的理解，还是刚才雷达的例子。假设现在有10个雷达信号警报，其中8个是真的轰炸机（P）来了，2个是大鸟（N）飞过，经过某分析员解析雷达的信号，判断出9个信号是轰炸机，剩下1个是大鸟，其中被判定为轰炸机的信号中，有1个其实是大鸟的信号（FP=1），而剩下8个确实是轰炸机信号（TP=8）。因此可以计算出FPR为0.5，TPR为1，而（0.5，1）就对应ROC曲线上一点。

手画ROC曲线的方法：
就是把横轴的刻度间隔设为N，纵轴的刻度间隔设为，N,P分别为负样本与正样本数量。然后再根据模型的输出结果降序排列，依次遍历样本，从0开始绘制ROC曲线，每遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线，每遇到一个负样本就沿横轴方向绘制一个刻度间隔的曲线，遍历完所有样本点以后，曲线也就绘制完成了。究其根本，其最大的好处便是不需要再去指定阈值寻求关键点了，每一个样本的输出概率都算是一个阈值了。当然，无论是工业界还是学术界的实现，基本都是用软件去实现。这里只当是对画线原理进行一个介绍。

代价曲线

ROC曲线的一个优点就是，它和测试样本的类别分布于与误分类代价无关，即无论测试样本的正反例比例如何变化、无论误分类代价如何变化，分类器的ROC曲线都是不变的。一个指定的（类别分布，误分类代价）称为一个operating condition。
换句话说，前面介绍的性能度量，大都隐式地假设了“均等代价”。如果实际处理问题中，我们面临的是一个非均等代价问题，ROC曲线不能直接反映出学习器的期望总体代价，而“代价曲线”则可以达到目的。

假设检验

统计过程一般分为三步：1提出问题。2 根据问题提出假设 H0 H1。 3 根据统计分布得出P值，根据P值接受或拒绝假设。
假设检验，方法包括 T检验、卡方检验、F检验等等。

卡方检验： 分类变量（离散） 比如 性别。

T检验： 数值变量 （连续） 2组及以内的数据。 比如 年龄。

方差分析：数值变量 （连续）多组数据。

如果数据不符合正态分布，秩和检验。

https://blog.csdn.net/qq_37059483/article/details/78614189
https://www.jianshu.com/p/2ca96fce7e81