数据挖掘-层次聚类与K均值算法的R实现

本次为学生时期所写的实验报告，代码程序为课堂学习和自学，对网络程序有所参考，如有雷同，望指出出处，谢谢！

基础知识来自教材：李航的《统计学习方法》

本人小白，仍在不断学习中，有错误的地方恳请大佬指出，谢谢！

一、层次聚类代码

1.前置预备函数

##############1：计算类与类之间的欧式距离##########
my_dist<-function(X,Y,p){
  #X，Y为两个类，p为变量的维数
  
  X=matrix(X,ncol=p)
  Y=matrix(Y,ncol=p)
  n1=nrow(X)
  n2=nrow(Y)
  
  if(n1==1&n2==1){           #两向量距离
    d=sqrt((X-Y)%*%t(X-Y))
  }else if(n1!=1&n2==1){     #单个向量到类（多个向量）之间的距离（最短距离法）
    d=min(as.matrix(dist(rbind(Y,X)))[-1,1])
  }else if(n1==1&n2!=1){
    d=min(as.matrix(dist(rbind(X,Y)))[-1,1])
  }else if(n1!=1&n2!=1){    #类（多向量）到类（多向量）之间的距离（最短距离法）
    d=min(as.matrix(dist(rbind(X,Y)))[-c(1:n1),1:n1])
  }

  d
}


##############2：寻找指定数据在原始数据矩阵中的位置##########
index_find<-function(X,data,p){      #data为给定的数据
  data=matrix(data,ncol=p)
  n=nrow(data)
  index=0
  for (j in 1:nrow(data)) {
    for (k in 1:nrow(X)) {
      TF=as.numeric(data[j,]==X[k,])
      if(sum(TF)==p){
        index=append(index,k)
      }
    }
  }
  index=index[-1]
}


##############3：为保证不出现分支，确定数据在聚类图中的特定排序#########
order_find<-function(indexlist,n){
  order=0
  #基本思想：从后往前，提取每一次聚类的两个类中含有数据较少的那个类中的数据
  
  for (k in length(indexlist):1) {
    nk=rep(NA,length(indexlist[[k]]))
    
    for (m in 1:length(indexlist[[k]])) {
      nk[m]=length(indexlist[[k]][[m]])
    }
    
    TF=as.numeric(nk==c(1,1))
    
    if(sum(TF)!=2){
      order=append(order,indexlist[[k]][[which.min(nk)]])
    }else if(sum(TF)==2){
      order=append(order,indexlist[[k]][[1]])
      order=append(order,indexlist[[k]][[2]])
    }
    if(length(order)==n+1){
      order=order[-1]
      break
    }
  }
  order
}

2.层次聚类代码编写

############编写层次聚类函数#####
my_clust<-function(X){    #使用最短距离法
  X=as.matrix(X)   #X转化为矩阵，便于后续计算
  n=dim(X)[1]       #n为样本数
  p=dim(X)[2]       #p为向量维数
  C_all=matrix(1:n,byrow=TRUE,nrow = n,ncol = n)   
#每一行记录每一次聚类后各向量对应的类别
  distance_record=rep(0,n-1)         #记录聚类时的最短距离

  merge=matrix(NA,ncol = 2,nrow = n-1)  
  #merge记录聚类情况：每一行表示一次聚类（概念设定与hclust输出模型中的“merge”相同）：
  #两负数表示两个单向量聚为一类，
  #一正一负表示负的那个单向量聚到正的数值所在的类
  #两正则表示两个大类聚合为一类
  
  indexlist<-list()  #记录每一次聚的两个类的标签
  
  #初始距离矩阵
  D_dist=matrix(0,nrow = n,ncol = n)
  D_dist[1:n,1:n] = as.matrix(dist(X))   #转化为矩阵格式（此时为对角矩阵且对角线元素为0）
  D_dist[D_dist==0]=round(max(D_dist))+1  #将0全部转化为最大值
  
  #返回距离最小的两个类
index=unique(which(D_dist[1:n,1:n]==min(D_dist[1:n,1:n])
arr.ind=TRUE)[1,])
  
  #第一次聚类：两个单向量聚为一类：故merge第一行为两负数
  merge[1,]=-index
  
  #记录距离最小值
  distance_record[1]=min(D_dist[1:n,1:n])
  
  #给新类加上标签
  for (m in 1:length(index)) {
    C_all[2:n,which(C_all[1,]==index[m])]=n+1
  }
  


  #开始迭代层次聚类
  i=2
  while (i<=n) {
    #各自把X属于同一类的提取出来
    dataselected=split(X, C_all[i,],drop = FALSE)
    classnum=length(dataselected)   #记录此时类别数
    D_dist=matrix(0,nrow = classnum,ncol = classnum)
    
    #计算各类之间的距离
    for (j in 1:classnum) {
      for (k in j:classnum) {
        if(j==k){
          D_dist[j,k]=0
        }else{
D_dist[j,k]=my_dist(dataselected[[j]],dataselected[[k]],p)
        }
      }
    }
    D_dist[D_dist==0]=round(max(D_dist),0)+1
    
    #记录此次迭代中各类间距离中的最小值
    distance_record[i]=min(D_dist[1:classnum,1:classnum])
    
    #记录距离最小的两类在列表中的下标
    index_pre=unique(which(D_dist[1:classnum,1:classnum]==min(D_dist[1:classnum,1:classnum]),arr.ind=TRUE)[1,])
    
    #返回距离最小的两类在原始数据矩阵中的下标
    index_list=list()
    for (j in 1:length(index_pre)) {
      data=dataselected[[index_pre[j]]]
      index_list[[j]]=index_find(X,data,p)
    }
    #index_list为长度为2的列表，元素分别为两个类对应的数据在原始矩阵中的位置
    index_list
    
    #indexlist记录此次聚类情况
    indexlist[[i-1]]=index_list
    
    #此次聚类中merge值确定
    n1=length(index_list[[1]])
    n2=length(index_list[[2]])
    if(n1==1&n2==1){
      for (j in 1:2) {
        merge[i,j]=-index_list[[j]]
      }
    }else if(n1!=1&n2==1){
      merge[i,1]=-index_list[[2]]
      merge[i,2]=C_all[i,][(index_list[[1]])[1]]-n
    }else if(n1==1&n2!=1){
      merge[i,1]=-index_list[[1]]
      merge[i,2]=C_all[i,][(index_list[[2]])[1]]-n
    }else if(n1!=1&n2!=1){
      merge[i,1]=C_all[i,][(index_list[[1]])[1]]-n
      merge[i,2]=C_all[i,][(index_list[[2]])[1]]-n
    }
    
    index=unlist(index_list)
    
    #在此次迭代对应的矩阵的行位置记录原始各数据对应的类别标签，标签相同的为同一类
    for (m in 1:length(index)) {
      C_all[(i+1):n,which(C_all[1,]==index[m])]=n+i
    }
    
    #收敛条件：全部聚为一类时收敛
    if(length(unique(C_all[i+1,]))==1){
      break
    }else{
      i=i+1
    }
  }
  
  list(C_all=C_all,merge=merge,height=distance_record,indexlist=indexlist)
}

3.检验代码

#数据：取iris中部分数据进行聚类
X=iris[1:20,-5]
X

#自编代码的结果
result=my_clust(X)
result$C_all       #每一次聚类的情况（数字相同的为同一类）
result$merge       #聚类过程记录
result$height      #每次聚类时的最短距离的值
result$indexlist   #聚类过程记录
n=nrow(X)       
order_find(result$indexlist,n)  #聚类图中的排序


#系统代码的结果
hc=hclust(dist(X),method = "single")
plot(hc) 
hc$merge
hc$height
hc$order
hc$labels
plot(hc) 

二、k均值算法代码

####函数编写
my_kmeans<-function(X,k,ddmax){
  X=as.matrix(X)
  n=dim(X)[1]
  p=dim(X)[2]
  C_all=matrix(NA,nrow = ddmax+1,ncol = n)
  C_all[1,]=rep(0,n)
  M=X[sample(1:n,k,replace=F),]
  
  i=2
  while (i<=(ddmax+1)) {
    #计算聚类C
    D=as.matrix(dist(rbind(X,M)))[1:n,(n+1):(n+k)]
    colnames(D)=NULL
    C_all[i,]=apply(D,1,which.min)
    
    #计算新的类中心M
    for (j in 1:k) {
      M[j,]=apply(X[which(C_all[i,]==j),],2,mean)
    }
    
    
    #可视化
    minx = min(X[,1])
    maxx = max(X[,1])
    miny = min(X[,2])
    maxy = max(X[,2])
    
    plot(X[which(C_all[i,]==1),1],X[which(C_all[i,]==1),2],
            pch =1,xlim = c(minx, maxx),ylim = c(miny, maxy),col=2)

    points(M[1,1],M[1,2],pch = 2,cex=1.5,col=2,lwd=2.5)
    
    for (j in 2:k) {
      points(X[which(C_all[i,]==j),1],X[which(C_all[i,]==j),2], pch = j,col=2*j)

      points(M[j,1],M[j,2],pch = 2*j,col=2*j,cex=1.5,lwd=2.5)
    }
    
    
    #收敛判断
    sum=sum(as.numeric(C_all[i-1,]==C_all[i,]))
    if(sum==n){
      C=C_all[i,]
      break
    }else{
      i=i+1
    }
  }
  list(C=C,M=M)
}

检验代码

####检验（iris数据集二维数据）####
X<-iris[,-c(3,4,5)]

#设k=3，规定聚为3类
result=my_kmeans(X,k=3,ddmax=50)
result
C_all=result$C
iris<-read.csv("F:/大三下/数据挖掘/UCI数据集/Iris/iris.data",header = F)
iris[,5][iris[,5]=="Iris-setosa"]=2
iris[,5][iris[,5]=="Iris-versicolor"]=3
iris[,5][iris[,5]=="Iris-virginica"]=1

#聚类准确率
corr_prop=sum(as.numeric(C_all==iris[,5]))/nrow(iris)
corr_prop

二、检验结果与分析

（一）层次聚类

1.自编函数

（1）聚类过程

> result$merge     #聚类过程记录

      [,1] [,2]

 [1,]  -18   -1

 [2,]   -5    1

 [3,]   -2  -13

 [4,]   -8    2

 [5,]  -10    3

 [6,]  -12    4

 [7,]   -3   -4

 [8,]  -20    6

 [9,]   -7    7

[10,]    5    9

[11,]   -9   10

[12,]    8   11

[13,]   -6  -19

[14,]  -11   12

[15,]  -17   14

[16,]   13   15

[17,]  -14   16

[18,]  -15   17

[19,]  -16   18

分析：此即为聚类过程描述：第一行：即18、1聚为一类； 第二行：5与第一个大类聚为一类；  第三行：即2、13聚为一个新的类......第十九行：16与聚成的第18类聚为一类。

（2）每次聚类时的类间距离（此算法中为最短距离）

> result$height    #每次聚类时的最短距离的值

 [1] 0.1000000 0.1414214 0.1414214 0.1732051 0.1732051 0.2236068 0.2449490 0.2645751

 [9] 0.2645751 0.2645751 0.3000000 0.3000000 0.3316625 0.3316625 0.3464102 0.3464102

[17] 0.3464102 0.4690416 0.5477226

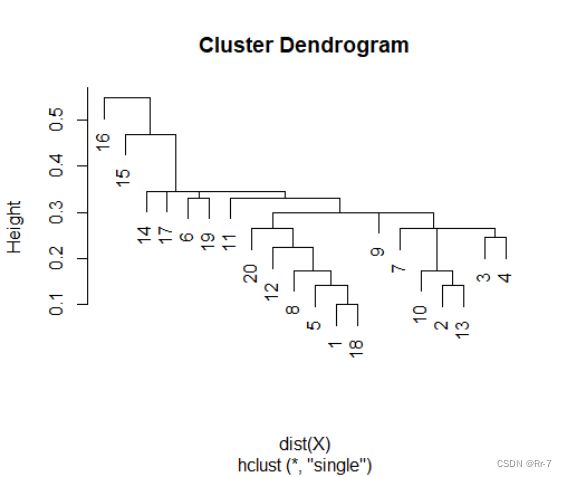
（3）聚类图中的排序

> order_find(result$indexlist,n)  #聚类图中的排序

[1] 16 15 14  6 19 17 11  6 19  1  5  8 12 18 20  9  2 10 13  7

分析：从后往前，提取每一次聚类的两个类中含有数据较少的那个类中的数据

2.系统自带hclust函数

（1）聚类过程

> hc$merge

      [,1] [,2]

 [1,]   -1  -18

 [2,]   -5    1

 [3,]   -2  -13

 [4,]   -8    2

 [5,]  -10    3

 [6,]  -12    4

 [7,]   -3   -4

 [8,]  -20    6

 [9,]    5    7

[10,]   -7    9

[11,]   -9   10

[12,]    8   11

[13,]   -6  -19

[14,]  -11   12

[15,]   13   14

[16,]  -17   15

[17,]  -14   16

[18,]  -15   17

[19,]  -16   18

（2）每次聚类时的类间距离（此算法中为最短距离）

> hc$height

 [1] 0.1000000 0.1414214 0.1414214 0.1732051 0.1732051 0.2236068 0.2449490 0.2645751

 [9] 0.2645751 0.2645751 0.3000000 0.3000000 0.3316625 0.3316625 0.3464102 0.3464102

[17] 0.3464102 0.4690416 0.5477226

（3）聚类图中的排序

> hc$order

 [1] 16 15 14 17  6 19 11 20 12  8  5  1 18  9  7 10  2 13  3  4

（4）聚类图

分析：综上可得自编函数的聚类结果与系统hclust的聚类结果一致，认为代码有效。

（二）k均值聚类

#此次聚类规定k=3

1.聚类结果：

> result

$C

  [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

 [37] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 3 1 3 1 3 1 3 3 3 3 3 3 1 3 3 3 3 3 3

 [73] 3 3 1 1 1 1 3 3 3 3 3 3 3 3 1 3 3 3 3 3 3 3 3 3 3 3 3 3 1 3 1 1 1 1 3 1

[109] 1 1 1 1 1 3 3 1 1 1 1 3 1 3 1 3 1 1 3 3 1 1 1 1 1 3 3 1 1 1 3 1 1 1 3 1

[145] 1 1 3 1 1 3

$M

           V1       V2

[1,] 6.812766 3.074468

[2,] 5.006000 3.418000

[3,] 5.773585 2.692453

2.聚类正确率

> corr_prop

[1] 0.82

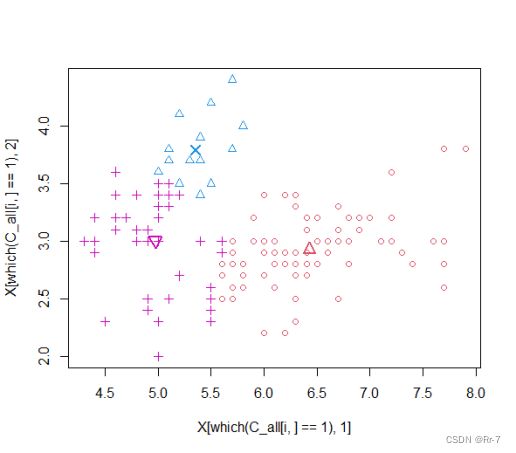
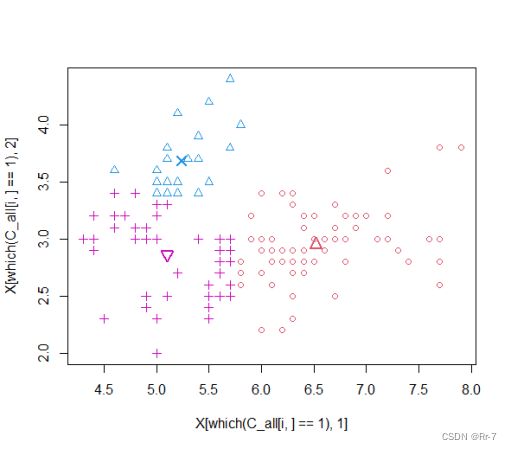
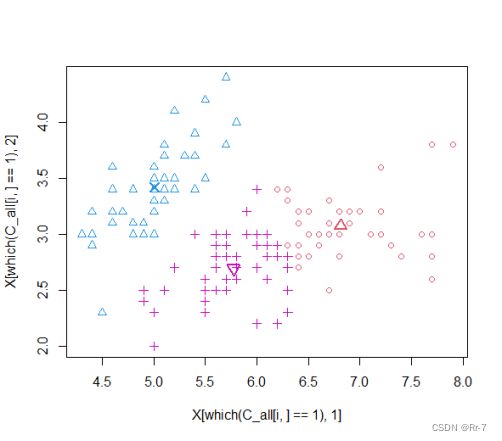
3.聚类过程部分散点图：

综上，聚类结果与原数据结果相比正确率较高，认为代码均有效。

三、小结

本次实验主要编写了层次聚类算法和k均值聚类算法，对于层次聚类过程：聚类结果非常清晰，而且唯一确定。但聚类结果非常依赖距离函数的选择，且聚类的时间空间复杂度均很大，在R运算时，若数据较大，运算时间将会变得很长。对于k均值聚类：使用逐步迭代的算法，计算出正确的分类使得损失函数达到最小，其聚类的时间空间复杂度相比层次聚类都大大减小。但其缺点是无法确定最佳的k，即无法使用先前的交叉验证算法，无法使用AIC、BIC准则等对k值进行选择。总的来说两种方法各有利弊，但从实际运用角度来看，k均值的使用更为广泛。