【LSSVM回归预测】基于matlab人工蜂群算法优化最小二乘支持向量机LSSVM数据回归预测【含Matlab源码 2213期】

⛄一、人工蜂群算法优化最小二乘支持向量机LSSVM简介

1 最小二乘支持向量机
最小二乘支持向量机是支持向量机的一种改进算法[9,10],它将SVM算法中的不等式约束转化为等式约束,采用最小二乘线性系统作为损失函数代替支持向量机所采用的二次规划方法,以下介绍了该方法的基本原理。


式(6)中取不同的核函数就生成不同的支持向量机(图1),目前使用最多的核函数主要有多项式核函数、线性核函数、径向基核函数(RBF)。由于RBF核函数结构简单,泛化能力强,这样需要优化的参数最少,只有核参数σ和正规化参数γ。

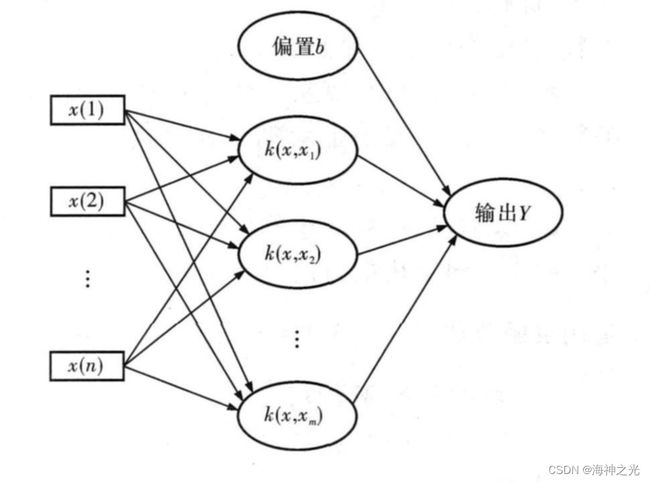
图1 支持向量机模型

2 人工蜂群算法
ABC算法中,由食物源位置代表优化问题的解,以此来寻找最优解[11,12]。蜂群具有3种类型的工蜂: 采蜜蜂、跟随蜂和侦察蜂。专业工蜂专门进行采集,守望蜂等待在蜂巢中观看同伴表演的摇摆舞,侦察蜂进行随机搜索。其中,专业工蜂和守望蜂的数量相等,都等于食物源的数量SN。每个解xi(i=1,2,…,SN)是一个D维的列向量,D代表优化参数的个数。经初始化后,蜜蜂开始进行循环搜索,当蜜蜂搜索到新解的适应度高于旧解的适应度,则采蜜蜂会记住自己新的解。跟随蜂会根据这些解的可能值Pi进行搜索,如果搜索到的解被更新,则侦查蜂就会放弃原来的解,用新的解来代替。

采蜜蜂根据当前位置进行新解的搜索,可以根据下式:

vij=xij+ϕij(xij-xkj) (9)

其中,k∈{1,2,…,SN},j∈{1,2,…,D}均随机选择,且k≠i。ϕij为[-1,1]之间的随机数。跟随蜂选择食物源的可能值可定义为:

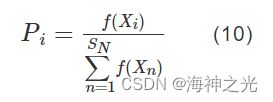
式中f(Xi)是第i个解的适应度值。如果解Xi更新失败,则说明这个解不能被优化,需要运用下式产生新的解来代替它:

Xi=Xmin+rand(0,1)(Xmax-Xmin) (11)

3 基于ABC算法的LSSVM参数优化
LSSVM参数γ和σ对其分类精度有较大的影响,通常采用参数空间穷尽搜索法对 LSSVM 的参数进行优化,其缺点是很难确定一个合理的参数范围。因此,笔者采用 ABC 优化 LSSVM 的参数,其整个优化步骤如下[13]:

a. 初始化ABC算法中的各种参数,食物源的数量SN、食物源的最大循环次和终止循环次数;

b. 设置ABC算法中的使用度函数,优化最小二乘支持向量机的目的是减少预测误差,因此适用度函数适用为f(Xi)=11)MSE,其中MSEi表示第i个解的LSSVM的均方根误差;

c. 初始化模型搜索范围,利用ABC算法对LSSVM模型进行优化。

⛄二、部分源代码

clc
close all
clear
format long

tic
%==============================================================
%%导入数据
data=xlsread(‘1.xlsx’);
[row,col]=size(data);
x=data(:,1:col-1);
y=data(:,col);
set=1; %设置测量样本数
row1=row-set;%
train_x=x(1:row1,:);
train_y=y(1:row1,:);
test_x=x(row1+1:row,:);%预测输入
test_y=y(row1+1:row,:);%预测输出
train_x=train_x’;
train_y=train_y’;
test_x=test_x’;
test_y=test_y’;

%%数据归一化
[train_x,minx,maxx, train_yy,miny,maxy] =premnmx(train_x,train_y);
test_x=tramnmx(test_x,minx,maxx);
train_x=train_x’;
train_yy=train_yy’;
train_y=train_y’;
test_x=test_x’;
test_y=test_y’;
%% 参数初始化
lb=[0.1 0.01];%参数c g的变化的最小值.
ub=[1000 100];%参数c g的变化的最大值.
maxgen=100; % 进化次数 300
sizepop=10; % 种群规模30
limit=3;
%%定义lssvm相关参数
type=‘f’;
kernel = ‘RBF_kernel’;
proprecess=‘proprecess’;
[global_x, fit_gen,global_fitness]=ABC(lb,ub,maxgen,sizepop,limit,train_x,train_yy,type,kernel,proprecess,test_x,test_y,miny,maxy,train_y);
%% 结果分析
plot(fit_gen,‘LineWidth’,2);
title([‘人工蜂群优化svm适应度曲线’,‘(终止代数=’,num2str(maxgen),‘)’],‘FontSize’,13);
xlabel(‘进化代数’);ylabel(‘误差适应度’);

bestc = global_x(1);
bestg = global_x(2);

gam=bestc;
sig2=bestg;
model=initlssvm(train_x,train_yy,type,gam,sig2,kernel,proprecess);%原来是显示
model=trainlssvm(model);%原来是显示
%求出训练集和测试集的预测值
[train_predict_y,zt,model]=simlssvm(model,train_x);
[test_predict_y,zt,model]=simlssvm(model,test_x);
%预测数据反归一化
train_predict=postmnmx(train_predict_y,miny,maxy);%预测输出
test_predict=postmnmx(test_predict_y,miny,maxy);
%计算均方差
trainmse=sum((train_predict-train_y).^2)/length(train_y)
%testmse=sum((test_predict-test_y).^2)/length(test_y)

figure
plot(test_predict,‘:og’)
hold on
plot(test_y,‘- *’)
legend(‘预测输出’,‘期望输出’)
title(‘网络预测输出’,‘fontsize’,12)
ylabel(‘函数输出’,‘fontsize’,12)
xlabel(‘样本’,‘fontsize’,12)
figure
plot(train_predict,‘:og’)
hold on
plot(train_y,‘- *’)
legend(‘预测输出’,‘期望输出’)
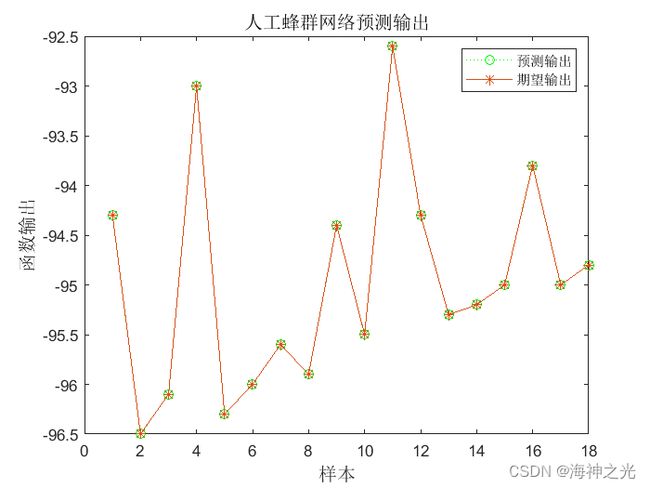
title(‘人工蜂群网络预测输出’,‘fontsize’,12)
ylabel(‘函数输出’,‘fontsize’,12)
xlabel(‘样本’,‘fontsize’,12)

toc %计算时间

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]杨日光,杨悦.基于人工蜂群算法优化LSSVM的蒸汽干度软测量[J].化工机械. 2013,40(02)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除