Leetcode第319场周赛题解

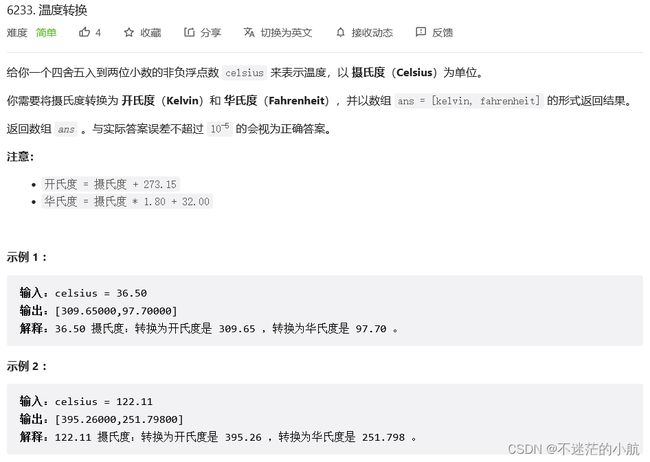
T1：LeetCode 2469. 温度转换

简单的模拟题：

代码一行搞定

class Solution {
public:
    vector convertTemperature(double celsius) {
        return {celsius + 273.15, celsius * 1.8 + 32};
    }
};

T2:LeetCode 2470. 最小公倍数为 K 的子数组数目

 

 发现这里数据范围比较小，直接枚举遍历就好

先枚举起点再枚举终点，枚举终点时边枚举边求最小公倍数

这里 a和b最小公倍数 = a * b / a和b的最大公约数

这样子时间复杂度的话就，在数据范围内可以过。

上代码

class Solution {
public:
    int gcd(int a, int b)
    {
        return b ? gcd(b, a % b) : a;
    }
    int subarrayLCM(vector& nums, int k) {
        int res = 0;

        for(int i = 0; i < nums.size(); i ++ ){
            int t = nums[i];//t存当前最小公倍数
            for(int j = i; j < nums.size(); j ++ ){
                t = t * nums[j] / gcd(t, nums[j]);
                if(t == k) res ++ ;
                else if(t > k) break;//及时跳出循环
            }
        }
        return res;
    }
};

T3：LeetCode 2471. 逐层排序二叉树所需的最少操作数目

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

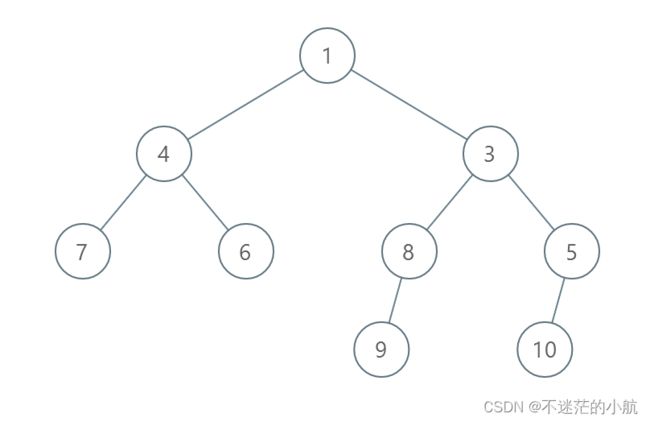
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

示例 2 ：

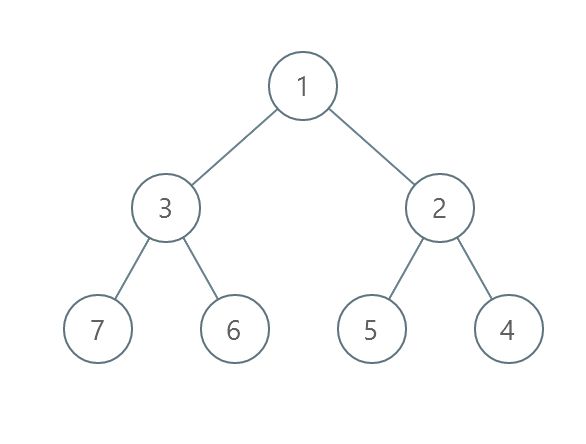
输入：root = [1,3,2,7,6,5,4]
输出：3
解释：
- 交换 3 和 2 。第 2 层变为 [2,3] 。 
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。 
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作，所以返回 3 。 
可以证明 3 是需要的最少操作数目。

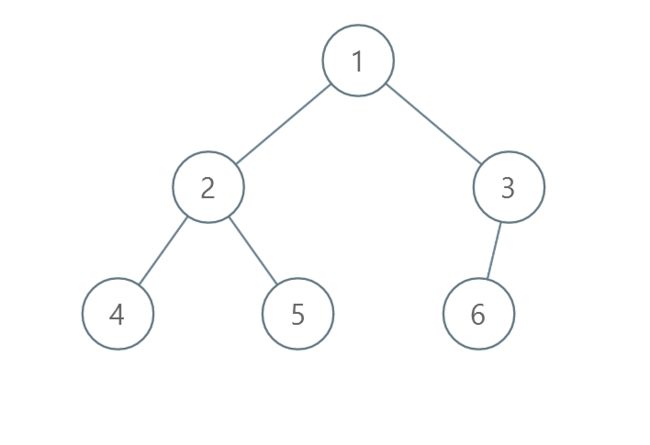
示例 3 ：

第三题压轴，感觉比第四题难

共两问：第一问求层数遍历，第二问将区间变成升序，每一次只能操作两个数，问最少操作多少次

第一问dfs，bfs都行，第二问，考的是环图，之前也没见过

在这里好好总结一下：

我们以位置建立图

假设原区间为2，1，4，5，3

这里建图规则为：第一个位置数1在原区间在2的位置，就从1往2连一条边

第二个位置数2在原区间在1的位置，就从2往1连一条边

第三个位置数3在原区间在5的位置，就从3往5连一条边

第四个位置数4在原区间在3的位置，就从4往3连一条边

第五个位置数5在原区间在4的位置，就从5往4连一条边

这样的话规则就是假设 在原数组中是第 j 的位置，那么我们就从 i 向 j 连一条边

保证了每个点的出度和入度都是1，那么必然会形成一个环，必然不会走到中间的点，因为这样某一点的入度就为2。

这样我们可以发现原区间我们可以将它看作是若干个环组成

因此，我们交换数字又有两种情况，第一种情况是交换的数不在一个环里，另一种情况是交换的数在一个环里。

当交换的数不在一个环里时，交换完后就结合成了一个环，如图

交换的数在一个环里时，交换操作会将一个环拆分成两个环，如图

 而我们的目标是将原数组变成升序，也就是变成个自环。

这样我们的题目就可以理解为：

给我们一堆环图，我们有两种操作

1.合并两个环

2.拆分一个环（拆成两个环）

目标是将环图拆成n个环，问最少要进行多少次操作。

再来分析，想要变成n个环，也就是说要多进行拆分操作，少合并，那我们可以统计一下当前有多少个环，假设有cnt个环的话，每拆一次最多增加一个环，则最少要拆次。

最后即为答案。

最后最后，我们求得环的数量即可。

上代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    vector p;

    int find(int x)// 默写并查集
    {
        if(p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
    int minimumOperations(TreeNode* root) {
        queue q;
        q.push(root);//插入头节点
        vector w, ls;//再定义数组存储层序遍历的序列，ls代表每一层的起点
        while(q.size())//当队列不空时
        {
            int sz = q.size();//求队列长度
            ls.push_back(w.size());//开始结点为w.size()
            for(int k = 0;k < sz; k ++ )//遍历每一层结点，每层的话有sz个结点
            {
                auto t = q.front();//每次取出来队头元素，接着删掉
                q.pop();
                w.push_back(t->val);//记录点的权值
                //判断如果有左右儿子的话，就遍历一下左右儿子
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
        }

        unordered_map pos;//记录每个点在原数组中的位置
        for(int i = 0; i < w.size(); i ++ )
        {
            pos[w[i]] = i;
            p.push_back(i);
        }

        ls.push_back(w.size());//给最后一层加上个终点
        for(int i = 0; i + 1 < ls.size(); i ++ )
            sort(w.begin() + ls[i], w.begin() + ls[i + 1]);//将每一层排个序
        

        int cnt = w.size();//接着统计当前有多少连通块
        for(int i = 0; i < w.size(); i ++ ){
            int a = find(i), b = find(pos[w[i]]);//第一个点为i，第二点为w[i]在原数组中的位置
            if(a != b)//判断一下如果合并的话
            {
                p[a] = b;
                cnt -- ;
            }
        }

        return w.size() - cnt;
    }
};

 第三题值得好好研究一下，代码实现上还用哈希表与并查集的知识。

本体涉及集合的合-->并查集

T4:LeetCode 2472. 不重叠回文子字符串的最大数目

 还是两个问题，第一个问题，预处理一下每个区间是不是回文串，第二个问题求能选择的最大数量用dp做

代表前 i 个字母最多可以拆出来多少个不重叠的回文串

这里的话就是一个dp问题，

第一种情况就是第i个字母不被选，那么答案就为

接下来的情况就是第i个字母被选，再枚举最后一段长度，如果是1，2，3，.......

当然我们在枚举的时候要考虑大等于k的情况

最后枚举一下最后一段长度，当最后一段长度为 时，这一类情况的最大值就是让前面尽可能取最多的回文串，即

具体的看一下代码吧

class Solution {
public:
    int maxPalindromes(string s, int k) {
        int n = s.size();
        vector> g(n + 1, vector(n + 1));//下标从1开始
        for (int len = 1; len <= n; len ++ ) {
            for (int i = 1; i + len - 1 <= n; i ++ ) {
                int j = i + len - 1;
                //一个字母的话一定是回文串
                if (s[i - 1] == s[j - 1] && (len <= 2 || g[i + 1][j - 1]))
                    g[i][j] = true;
            }
        }

        vector f(n + 1);
        for (int i = 1; i <= n; i ++ ) {
            f[i] = f[i - 1];
            for (int j = i - k; j >= 0; j -- ) {//保证最少有k个字母
                if (g[j + 1][i]) {//当j + 1 到 i 是回文串
                    f[i] = max(f[i], f[j] + 1);
                }
            }
        }

        return f[n];
    }
};

总结：T2：最大公倍数求法

T3：层序遍历，环图

T4：判断回文，区间dp