层次分析法
层次分析法
一、层次分析法概述
层次分析法(AHP法) 是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来,用决策者的经验判断各衡
量目标能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每
个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以
用定量方法解决的课题。
二、层次分析法的步骤
- 建立层次结构模型
- 构造判断(成对比较)矩阵
- 层次单排序及其一致性检验
- 层次总排序及其一致性检验
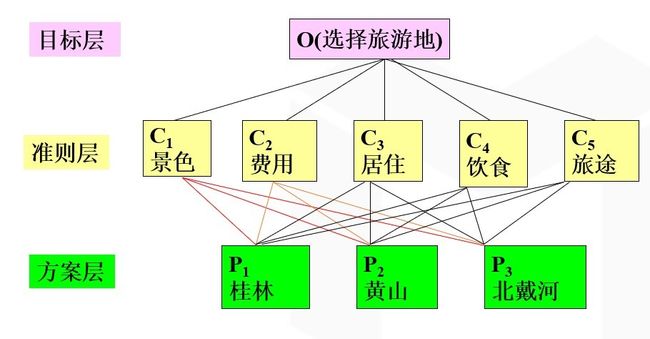
1.建立层次结构模型
将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分
为最高层、中间层和最低层,绘出层次结构图。
2.构造判断(成对比较)矩阵
层次分析法中构造判断矩阵的方法是一致矩阵法,即:不把所有因素放在一起比较,而是两两相互比较;对此时采用相对尺度,以尽可能减少性质不同因素相互比较的困难,以提高准确度。

3.层次单排序及其一致性检验
对应于判断矩阵最大特征根λmax的特征向量,经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值,这一过程称为层次单排序。
能否确认层次单排序,需要进行一致性检验,所谓一致性检验是指对A确定不一致的允许范围。
定义一致性指标:
C I = λ − n n − 1 CI=\frac{\lambda-n}{n-1} CI=n−1λ−n
- CI=0,有完全的一致性
- CI接近于0,有满意的一致性
- CI 越大,不一致越严重
为衡量CI 的大小,引入随机一致性指标 RI。
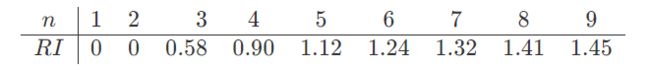
定义一致性比率:
C R = C I R I CR=\frac{CI}{RI} CR=RICI
一般,当一致性比率 C R < 0.1 CR<0.1 CR<0.1时,认为A的不一致程度在容许范围之内,有满意的一致性,通过一致性检验。
可用其归一化特征向量作为权向量,否则要重新构造成对比较矩阵A,对 a i j a_{ij} aij 加以调整
4.层次总排序及其一致性检验
层次总排序*:计算某一层次所有因素对于最高层(总目标)相对重要性的权值
例如:
记第2层(准则)对第1层(目标)的权向量为
w ( 2 ) = ( 0.263 , 0.475 , 0.055 , 0.090 , 0.110 ) T w^{(2)}= (0.263,0.475,0.055,0.090,0.110)^{T} w(2)=(0.263,0.475,0.055,0.090,0.110)T
同样求第3层(方案)对第2层每一元素(准则)的权向量
方案层对C1(景色)的成对比较阵B1
1 2 5 1 / 2 1 2 1 / 5 1 / 2 1 \begin{matrix} 1 & 2 & 5 \\\\ 1/2 & 1 & 2 \\\\ 1/5 & 1/2 & 1 \\\\ \end{matrix} 11/21/5211/2521
计算得,权向量$w1^{(3)}=(0.595,0.277,0.129) $
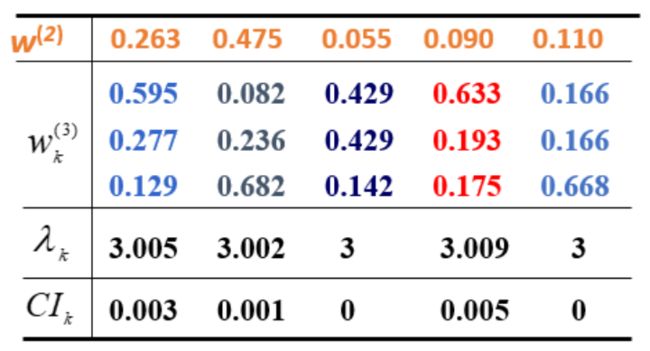
R I = 0.58 ( n = 3 ) RI=0.58 (n=3) RI=0.58(n=3), C I k CI_k CIk 均可通过一致性检验。
方案P1对目标的组合权重为 0.595 × 0.263 + 0.082 × 0.475 + ⋅ ⋅ ⋅ + 0.166 × 0.110 = 0.294 0.595×0.263+0.082×0.475+···+0.166×0.110=0.294 0.595×0.263+0.082×0.475+⋅⋅⋅+0.166×0.110=0.294
方案层对目标的组合权向量为 ( 0.294 , 0.246 , 0.456 ) T (0.294, 0.246, 0.456)^T (0.294,0.246,0.456)T
三、层次分析法的优缺点
1.优点
- 系统性——将对象视作系统,按照分解、比较、判断、综合的思维方式进行决策。成为成为继机理分析、统计分析之后发展起来的系统分析的重要工具;
- 实用性——定性与定量相结合,能处理许多用传统的最优化技术无法着手的实际问题,应用范围很广,同时,这种方法使得决策者与决策分析者能够相互沟通,决策者甚至可以直接应用它,这就增加了决策的有效性;
- 简洁性——计算简便,结果明确,具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该法的基本步骤,容易被决策者了解和掌握。便于决策者直接了解和掌握。
2.缺点
- 囿旧——只能从原有的方案中优选一个出来,没有办法得出更好的新方案;
- 粗略——该法中的比较、判断以及结果的计算过程都是粗糙的,不适用于精度较高的问题。
- 主观——从建立层次结构模型到给出成对比较矩阵,人主观因素对整个过程的影响很大,这就使得结果难以让所有的决策者接受。当然采取专家群体判断的办法是克服这个缺点的一种途径。
四、层次分析法代码
clc;clear
A=[1 1/5 1 1/5 1/6 1/6
5 1 5 1/2 1/2 1/2
2 1/5 1 1/4 1/6 1/4
5 1/2 4 1 1/2 1/2
6 2 6 2 1 1
6 2 4 2 1 1]
[n,n]=size(A);
[V,D]=eig(A);%求得特征向量和特征值
%求出最大特征值和它所对应的特征向量
tempNum=D(1,1);
pos=1;
for h=1:n
if D(h,h)>tempNum
tempNum=D(h,h);
pos=h;
end
end
w=abs(V(:,pos));
w=w/sum(w);
t=D(pos,pos);
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);
%以下是一致性检验
CI=(t-n)/(n-1);
RI=[0 0 0.58 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败,请重新进行评分!');
end
A = 6×6
1.0000 0.2000 1.0000 0.2000 0.1667 0.1667
5.0000 1.0000 5.0000 0.5000 0.5000 0.5000
2.0000 0.2000 1.0000 0.2500 0.1667 0.2500
5.0000 0.5000 4.0000 1.0000 0.5000 0.5000
6.0000 2.0000 6.0000 2.0000 1.0000 1.0000
6.0000 2.0000 4.0000 2.0000 1.0000 1.0000
准则层特征向量w=
0.0425
0.1677
0.0546
0.1580
0.2976
0.2797
准则层最大特征根t=
6.0846
此矩阵的一致性可以接受!
CI=
0.0169
CR=
0.0134