《统计学习方法》Chapter.6.1 逻辑斯谛回归(Logistic Regression)
Logistic回归
Logistic分布
设 X X X是连续随机变量, X X X服从逻辑斯蒂分布是指 X X X具有下列分布函数和密度函数:
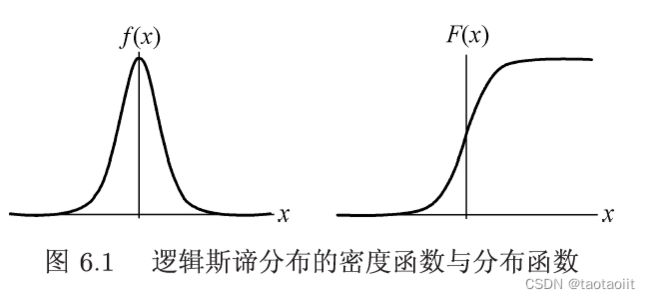
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) / r f ( x ) = F ′ ( x ) = e − ( x − μ ) / r γ ( 1 + e − ( x − μ ) / r ) 2 F(x) = P(X\leq x) = \frac{1}{1+e^{-(x-\mu)/r}}\\ f(x) = F^{'}(x) = \frac{e^{-(x-\mu)/r}}{\gamma (1+e^{-(x-\mu)/r})^2}\\ F(x)=P(X≤x)=1+e−(x−μ)/r1f(x)=F′(x)=γ(1+e−(x−μ)/r)2e−(x−μ)/r
其中, μ \mu μ为位置参数, γ \gamma γ为形状参数。
二项Logistic回归模型
这里虽然说是回归模型,但是本质上是一个线性分类模型
定义
二项逻辑斯蒂回归模型是如下的条件概率分布:
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x + b ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ⋅ x + b ) P(Y=1|x) = \frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)}\\ P(Y=0|x) = \frac{1}{1+exp(w\cdot x+b)} P(Y=1∣x)=1+exp(w⋅x+b)exp(w⋅x+b)P(Y=0∣x)=1+exp(w⋅x+b)1
这里, x ∈ R n x\in R^n x∈Rn是输入, Y ∈ { 0 , 1 } Y\in \{0,1\} Y∈{0,1}是输出, w ∈ R n w\in R^n w∈Rn和 b ∈ R b \in R b∈R是参数, w w w成为权值向量, b b b成为偏置, w ⋅ x w\cdot x w⋅x为 w w w与 x x x的内积。
有时为了方便,将权值向量和输入向量加以扩充,即:
w = ( w ( 1 ) , w ( 2 ) , . . . , w ( n ) , b ) T , x = ( x ( 1 ) , x ( 2 ) , . . . , x ( n ) , 1 ) w = (w^{(1)},w^{(2)},...,w^{(n)},b)^T,\\ x = (x^{(1)},x^{(2)},...,x^{(n)},1) w=(w(1),w(2),...,w(n),b)T,x=(x(1),x(2),...,x(n),1)
这时,逻辑斯蒂回归模型如下:
P ( Y = 1 ∣ x ) = e x p ( w ⋅ x ) 1 + e x p ( w ⋅ x ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ⋅ x ) P(Y=1|x) = \frac{exp(w\cdot x)}{1+exp(w\cdot x)}\\ P(Y=0|x) = \frac{1}{1+exp(w\cdot x)} P(Y=1∣x)=1+exp(w⋅x)exp(w⋅x)P(Y=0∣x)=1+exp(w⋅x)1
思想
事件发生的几率
一个时间发生的几率是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是 p p p,那么该事件的几率是:
p 1 − p \frac{p}{1-p} 1−pp
对数几率为:
l o g i t ( p ) = l o g p 1 − p {\rm logit}(p) = {\rm log \,}\frac{p}{1-p} logit(p)=log1−pp
逻辑斯蒂回归模型的对数几率
对于逻辑斯蒂回归而言,将公式其带入对数几率模型中得到:
l o g P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w ⋅ x {\rm log\,}\frac{P(Y=1|x)}{1-P(Y=1|x)}=w\cdot x log1−P(Y=1∣x)P(Y=1∣x)=w⋅x
即逻辑回归模型中,输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数。
换一个角度看,考虑对输入 x x x进行分类的线性函数 w ⋅ x w\cdot x w⋅x,其值域为实数域。线性函数的值越接近正无穷, Y = 1 Y=1 Y=1的概率就越接近 1 1 1;线性函数的值越接近负无穷, Y = 1 Y=1 Y=1的概率就越接近 0 0 0.这种模型即为逻辑回归模型。
模型参数估计
对于给定的训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1,y1),(x2,y2),...,(xN,yN)},其中, x i ∈ R n , y i ∈ R n , y i ∈ { 0 , 1 } x_i \in R^n,y_i\in R^n,y_i \in \{0,1\} xi∈Rn,yi∈Rn,yi∈{0,1},可以用极大似然估计模型参数,从而得到逻辑斯蒂回归模型。
设:
P ( Y = 1 ∣ x ) = π ( x ) , P ( Y = 0 ∣ x ) = 1 − π ( x ) P(Y=1|x)=\pi(x), P(Y=0|x)=1-\pi(x) P(Y=1∣x)=π(x),P(Y=0∣x)=1−π(x)
似然函数为:
∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ] 1 − y i \prod_{i=1}^{N}{[\pi(x_i)]^{y_i}[1-\pi(x_i]^{1-y_i}} i=1∏N[π(xi)]yi[1−π(xi]1−yi
对数似然函数为:
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ L(w) &= \sum_{…
对 L ( w ) L(w) L(w)求极大值,得到 w w w的估计值。
这样,问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降法及拟牛顿法。
假设 w w w的极大似然估计值为 w ^ \hat{w} w^,那么学到的逻辑斯蒂回归模型为
P ( Y = 1 ∣ x ) = e x p ( w ^ ⋅ x ) 1 + e x p ( w ^ ⋅ x ) P ( Y = 0 ∣ x ) = 1 1 + e x p ( w ^ ⋅ x ) P(Y=1|x)=\frac{{\rm exp}(\hat{w}\cdot x)}{1+{\rm exp}(\hat{w}\cdot x)}\\ P(Y=0|x)=\frac{1}{1+{\rm exp}(\hat{w}\cdot x)} P(Y=1∣x)=1+exp(w^⋅x)exp(w^⋅x)P(Y=0∣x)=1+exp(w^⋅x)1
多项Logistic回归
对于Logistic回归应用于多分类问题,可以将问题看成多项分布,构造多项逻辑斯蒂回归模型,当然也可放在一般二分类模型推广到多分类模型的情况中考虑,一般的二分类推广到多分类模型的方法有:one-vs-rest,one-vs-one,error correcting output codes.
具体解释请见:https://taotaoiit.blog.csdn.net/article/details/127268199?spm=1001.2014.3001.5502
假设离散型随机变量 Y Y Y的取值集合是 { 1 , 2 , . . . , K } \{1,2,...,K\} {1,2,...,K},那么多项逻辑斯蒂回归模型是:
P ( Y = k ∣ x ) = e x p ( w k ⋅ x ) 1 + ∑ k = 1 K − 1 e x p ( w k ⋅ x ) , k = 1 , 2 , . . . , K − 1 P ( Y = K ∣ x ) = 1 1 + ∑ k = 1 K − 1 e x p ( w k ⋅ x ) P(Y=k|x) = \frac{{\rm exp}(w_k \cdot x)}{1+\sum_{k=1}^{K-1}{{\rm exp}(w_k\cdot x)}},\;k=1,2,...,K-1\\ P(Y=K|x) = \frac{1}{1+\sum_{k=1}^{K-1}{{\rm exp}(w_k\cdot x)}} P(Y=k∣x)=1+∑k=1K−1exp(wk⋅x)exp(wk⋅x),k=1,2,...,K−1P(Y=K∣x)=1+∑k=1K−1exp(wk⋅x)1
这里, x ∈ R n + 1 , w k ∈ R n + 1 x\in R^{n+1},w_k\in R^{n+1} x∈Rn+1,wk∈Rn+1
对于多项逻辑斯蒂回归的参数估计可以应用极大化似然函数思想。
代码实例
import numpy as np
from sklearn import linear_model, datasets
from sklearn.model_selection import train_test_split
# 调用鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
Y = iris.target
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.3)
# 数据标准化
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
X_train_std = ss.fit_transform(X_train)
X_test_std = ss.fit_transform(X_test)
lg = linear_model.LogisticRegression()
lg.fit(X_train_std,Y_train)
lg.score(X_test_std,Y_test)
0.9777777777777777