形式语言与自动机 02 Preliminaries

Preliminaries

SETS

• Union
• Intersection
• Difference
• Complement 补

$\overline{\overline{A}}=A$

$\overline{A\cup B}=\overline{A}\cap \overline{B}$

$\overline{A\cap B}=\overline{A}\cup \overline{B}$

Empty, Null Set

空集 $\varnothing$

Subset and Proper Subset

Disjoint Sets

$A\cap B=\varnothing$

Set Cardinality 集合的势

$|A|$ 表示集合A中的元素个数

Powersets 幂集

$S=a,b,c$

$P(S)=2^S=S=\{\varnothing ,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}$

Observation $ |2^S| = 2^{|S|}$

笛卡尔乘积

$|A\times B|=|A|\times |B|$

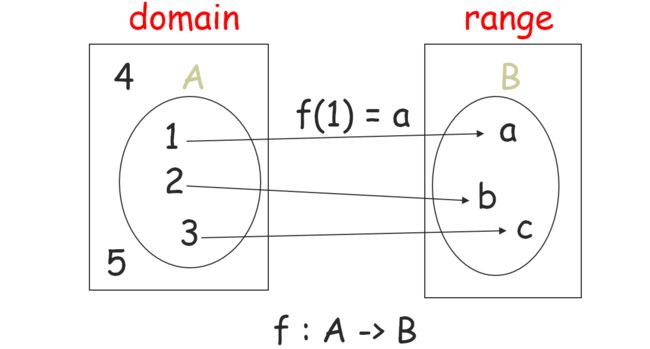
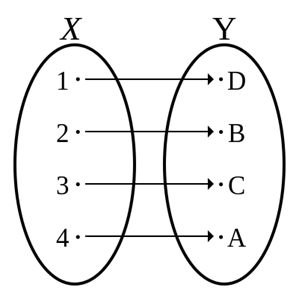
FUNCTIONS

$A->B$

• If A = domain

  then f is a total function

  otherwise f is a partial function

• f : A -> B is a bijection 双射

  • f is total
  • for all a and a’ in A, a != a’ implies f(a) != f(a’)
  • for all b in B, there is a in A with f(a) = b

Big O Notation

$\Omega (n)$ 下界

$O(n)$ 上界

$\theta (n)$

rate of growth

RELATIONS

Given two sets, A and B, a relation R is any subset of A x B, in orther words, $R\subseteq A\times B$

Equivalence Classes

• Reflexive: x R x
• Symmetric: x R y -> y R x
• Transitive: x R y and y R z -> x R z

等价关系

等价类

• partial order 偏序关系

  reflexive， transitive and antisymmetric

• total order 全序关系

• linear order 线性关系

GRAPHS

• walk
• path 无重复边
• simple path 无重复节点
• cycle 环
• simple cycle 仅根节点重复

、

• 可达性

  

Trees

root，leaf，height

PROOF TECHNIQUES

• 数学归纳
• 反证法
• 鸽巢原理 （Pigeon Hole Principle）

Languages

• A language is a set of strings
• String: A sequence of letters/symbols
  • Examples: “cat”,“dog”…
  • Symbols are defined over an alphabet:

Alphabets and Strings

String Operations

• Connection
• Reverse

String length

• Length: The length of a string x is the number of symbols contained in the string x, denoted by |x|

  $w=a_1{a}_2{a}_3...a_n\to |w|=n$

The Empty String

• A string with no letters: $\lambda$ or $ϵ$
• Observations: $|\lambda |=0$

$\lambda w=w\lambda =w$

Substring

Prefix and Suffix (x = ysz)

Another Operation

$w^n=www...w$ (n个w)

$(abbs{)}^2=abbaabba$

$w^0=\lambda$

Solve equation 011x = x011

• If $x=\lambda$ ，then ok.

• If $|x|=1$,then no solution.

• If $|x|=2$,then no solution.

• If $|x|\ge 3$,then x = 011y . Hence,

  011x = 011y011. So, x = y011.

  Hence, 011y = y011.

• $x=(011{)}^{k}fork\ge 0$

The * Operation

$\sum ^* : $ the set of all possible strings from alphabet $ \sum$

Example:

$\sum =\{a,b\}$

${\sum }^{\ast }=\{\lambda ,a,b,aa,ab,ba,bb,aaa...\}$

The + Operation

${\sum }^{+}={\sum }^{\ast }-\{\lambda \}$

Languages

A language is a set of strings, is any subset of ${\sum }^{\ast }$

Note that: $\varnothing =\{\}\ne \lambda$

Operations on Languages

Reverse

$L^R=\{w^R:w\in L\}$

Concatenation

$L_1{L}_2=\{xy:x\in L_1,y\in L_2\}$

Anothor Operation

$L^n=LL...L$

Special case： $L^0=\{\lambda \}$

Star-Closure(Kleene *)

$L^* = L^0 \cup L^1 \cup L^2 … L^n $

$L^{+}=L^{\ast }-\{\lambda \}$

补充

证明1：

$R\cup (S\cap T)=(R\cup S)\cap (R\cup T)$

$begin:$

当：

$E:=R\cup (S\cap T)F:=(R\cup S)\cap (R\cup T)$

$x\in R\cup (S\cap T)$

$x\in Rorx\in (S\cap T)$

$x\in R\cup Sandx\in R\cup T$

$x\in (R\cup S)\cap (R\cup T)$

仅当：

bulabula…

$end$

证明2：

不存在整数对a和b,使得 $a\mathrm{m}\mathrm{o}\mathrm{d}b=b\mathrm{m}\mathrm{o}\mathrm{d}a$

当需要处理成双的对象时，利用对称性常常有可能简化对象之间的关系，例如假设a

更一般的整数归纳法

1. 利用多个基础情形，对于某个$j>i$,证明$S(i),S(i+1)...S(j)$

2. 证明$S(n+1)$时，利用所有命题

   $S(i),S(i+1),...S(n)$

   而不是只利用$S(n)$

• 结构归纳法
• 互归纳

证明3 判定一个给定的串是否属于某个具体语言的提问

如果$\sum$是字母表，$L$是$\sum$ 上的语言，问题$L$就是：给定 ${\sum }^{\ast }$中的一个串$\omega$ ，判定串$\omega$是否属于L

"问题"的定义的一个可能不令人满意的方面是：人们常常不认为问题是判定问题（以下是否为真），而是认为是计算或者变换某个输入的请求（找出完成任务的最佳方法）