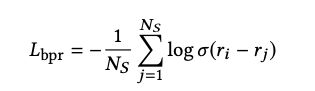【推荐算法论文阅读】Recurrent Neural Networks with Top-k Gains for Session-based Recommendations

本文是一篇很好的讲述进行梯度下降和参数更新时，困难样本、简单样本与梯度消失之间的关系，以及如何设置使简单样本对平均梯度的影响更小。

一、sampling the output

在每个训练步骤中，GRU4Rec 将会话中当前事件的项目（由 one-hot 向量表示）作为输入。 网络的输出是项目的一组分数，对应于它们成为会话中下一个项目的可能性。

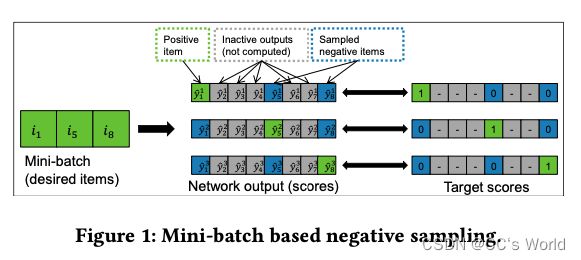
GRU4Rec 引入了基于mini-batch的采样。 对于mini-batch中的每个example，相同mini-batch的其他examples作为负样本。

排序损失的一个特性是，只有当target item的分数没有大幅超过负样本的分数时才会进行学习，否则项目已经处于正确的顺序，因此没有什么可学习的。

因此，在抽样的过程中，将得分高的item包含在负样本中至关重要。热门item在许多情况下通常得分很高，因此基于人气的抽样是一种很好的抽样策略。mini-batch抽样基本上是一种基于流行度的抽样形式，因为训练会遍历所有事件，因此一个item作为负样本的概率与其流行度成正比。

基于流行度的采样的问题在于，在算法学习将target item排在流行item之上以后，学习会减慢，因此对于长尾高分item的排序仍然可能不准确。另一方面，由于大量低分负样本，均匀采样会减慢学习速度，但如果无限期地训练，可能会产生总体上更准确的模型。根据我们的经验，基于流行度的抽样通常会产生更好的结果。

将抽样与mini-batch联系起来有许多好处，但也有以下三个限制：

1. Mini-batch 规模一般较小，从几十到几百不等。 如果项目的数量很大，那么小样本量会进一步阻碍包含所有高分负样本的机会。
2. Mini-batch 大小对训练有直接影响。 例如。 我们发现使用较小的小批量 (30-100) 进行训练会产生更准确的模型(这是因为最后取的是平均数，所以大量低分样本对梯度的贡献比较小，后面会详细说明)，但由于并行化，在 GPU 上使用较大的训练更快。
3. 抽样方法本质上是基于流行度的，这通常是一个很好的策略，但可能不是对所有数据集都是最优的。

因此本文提出了一种新的sample方法：在每个batch中，以mini-batch sample的方式采样$N_B-1$个负样本，再以任意一种方式采样$N_A$个共享的负样本。

二、loss fuction design

2.1 ranking loss： Top1 & BPR

2.1.1 Top1 loss

Top1 Loss是由两部分组成的启发式组合损失。 第一部分旨在将目标分数推高到所有样本分数之上，而第二部分将负样本的分数降低到零。 后者充当正则化器，但不是直接约束模型权重，而是惩罚负例的高分：

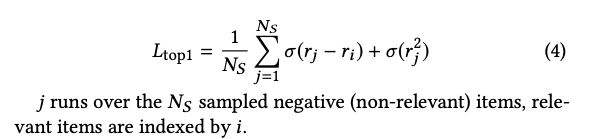
2.2.2 BPR Loss

2.2.3 梯度消失问题

对于成对损失，人们通常希望得到高分的负样本，因为这些样本会产生高梯度。 或者直观地说，如果负样本的分数已经远低于目标的分数，那么就不再可以从该负样本中学到任何东西了。

同时，梯度总是被负样本的总数打折。 通过增加样本数量，不相关样本的数量比包含相关样本的数量增加得更快，因为大多数项目作为负样本是不相关的。 对于非基于流行度的抽样和样本数多的情况尤其是这样。 因此，随着样本数量的增加，这些损失的梯度开始消失，这是违反直觉的，并且损害了算法的潜力。

这两种损失函数主要缺点是会发生梯度消失的现象，如当 $r_j<<r_i$ 时，$\sigma (r_j-r_i)和1-\sigma (r_i-r_j)$ 都会趋近于 0，从而导致梯度消失；同时对负样本取平均值会加速这种梯度消失的现象(样本量越多，平均值越小)。

2.2 ranking-max loss fuction

为了克服随着样本数量增加梯度消失的问题，论文提出了基于 pairwise 的 listwise 损失函数框架。 这个想法是将目标分数与最相关的样本分数（样本中的最大分数）进行比较。即：

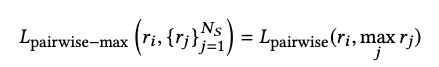
最大选择是不可微的，因此不能与梯度下降一起使用。 因此，我们使用 softmax 分数来保持可微性。 在这里，softmax 变换仅用于负例，因为我们是从负例中的最大分数来看的。 这自然会引出来损失函数，其中每个负样本都与其获得最大分数的可能性成正比。 基于这个总体思路，我们现在推导出 TOP1-max 和 BPR-max 损失函数。

对最大选择的连续逼近需要对由相应的 softmax 分数 $s_j$ 加权的各个损失求和，即：


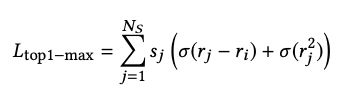
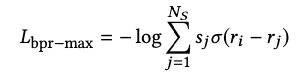
其中，$s_j$是softmax后的分数，得分越低，称为困难样本的概率就越低。在loss函数中，$s_j$就可以相当于权重，当 $r_j$ 较小时，$s_j$ 也会较小(趋近于 0)，样本 j 类似于被忽略，所以不会减少整体的梯度。

当$r_i$较小时，权重分布较为均匀，实际得分高的将会得到更多关注；当$r_i$较大时，得分高的才会产生较大的权重，从而得到更多关注。这有利于模型的训练。

如果 $r_j$ 远低于负样本的最大值，它的权重将几乎为零，并且更多的权重将放在分数接近最大值的示例上。 这解决了更多样本梯度消失的问题，因为不相关的样本将被忽略，而梯度将指向相关样本的梯度。 当然，如果所有样本都不相关，梯度会接近于零，但这不是问题，因为如果目标分数大于所有样本分数，则没有什么可学习的。

TOP1-max 和 BPR-max 的梯度信息均和 softmax score 成比例，这意味着只有 score 较大的 item 会被更新，因为如果负样本的分数很低，则不需要更新。 如果一个样本的分数远高于其他样本的分数，它将是唯一更新的，并且梯度将与目标和样本分数之间的成对损失的梯度一致。这样的好处在于模型训练过程中会一直推动 target 往排序列表的顶部前进，而常规的 TOP1 和 BPR 在 target 快接近顶部的时候，平均梯度信息更小了，更新几乎停滞，这样很难将 target 推至顶部。

BPR-max with score regularization

受 TOP1 添加正则项的启发，对 BPR 添加正则项，同样能提高模型的表现。

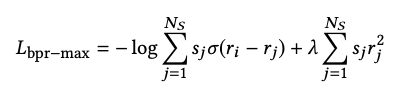
参考资料

GRU4Rec2 《Recurrent Neural Networks with Top-k Gains for Session-based Recommendations》