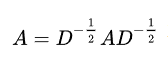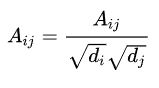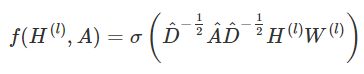GCN理解

关于GCN的原文介绍，可以参照github上面GRAPH CONVOLUTIONAL NETWORKS
相关的论文：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

1.GCN 为何而生

在具体了解GCN内部的模型之前，首先介绍一下它的作用，由于GCN公式的具体数学推导过于繁杂，在此不在介绍。

深度学习一直都是被几大经典模型给统治着，如CNN、RNN等等，它们无论在CV还是NLP领域都取得了优异的效果。GCN的发明是因为人们发现了很多CNN、RNN无法解决或者效果不好的问题——图结构的数据。

由此可以首先想到CNN和RNN的作用：

1. 关于CNN
   图像识别，对象是图片，是一个二维的结构，人们发明CNN这种模型来提取图片的特征。CNN的核心在于它的kernel，kernel是一个个小窗口，在图片上平移，通过卷积的方式来提取特征。平移不变性和参数共享，是CNN的精髓所在。
2. 关于RNN
   它的对象是自然语言这样的序列信息，是一个一维的结构，RNN就是专门针对这些序列的结构而设计的，使得序列前后的信息互相影响，从而很好地捕捉序列的特征。

在想到CNN和RNN的作用之后，由于他们的对象都有维度的概念，结构很规则。但是生活中有这样一种结构——图结构，一般来说是非常不规则的，甚至可以说没有维度概念，每一个节点周围结构可能都是独立的。因此，这种结构使得CNN和RNN无法发挥作用，GCN应运而生。

GCN，图卷积神经网络，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图结构数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding）。

2.GCN 如何发挥作用

2.1 GCN概述

在了解了GCN究竟从事哪个方面任务之后，具体来介绍一下GCN内部。

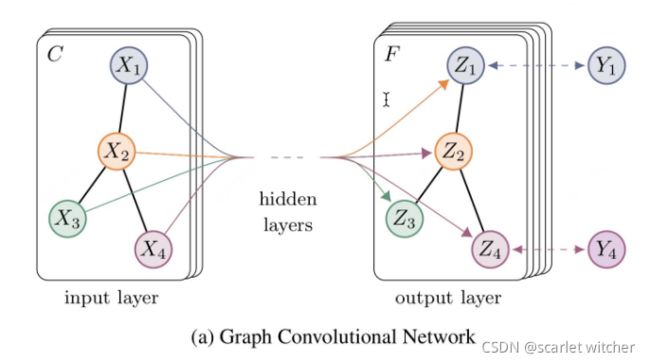
我们可以根据这个GCN的图看到，一个拥有 C 个input channel的graph作为输入，经过中间的hidden layers，得到 F 个 output channel的输出。图卷积网络主要可以由两个级别的作用变换组成：

• graph level
  例如说通过引入一些形式的pooling 操作然后改变图的结构，但是本次并没有进行这个级别的操作，所以看到上图我们的网络结构的输出和输出的graph的结构是一样的。
• node level
  通常说node level的作用是不改变graph的结构的，仅通过对graph的特征/信号（features/signals） X作为输入：一个 N * D 的矩阵( N: 输入图的nodes的个数， D：输入的特征维度) ，得到输出 Z：一个 N * F 的矩阵( F： 输出的特征维度)。

a) 一个特征描述（feature description）X_i : 指的是每个节点 X_i 的特征表示
b) 每一个graph 的结构都可以通过邻接矩阵 A 表示

例如下图：G = V * E 其中 V 代表节点， E 代表边

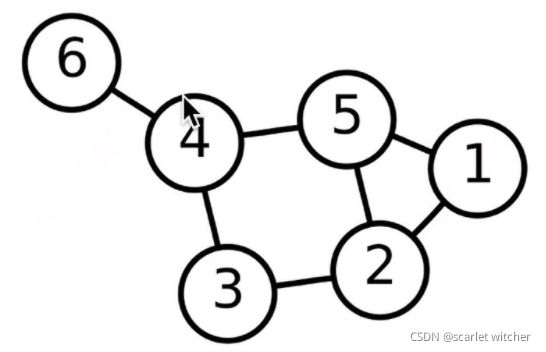
通过上面这个图结构，可以容易写出邻接矩阵A

网络中间的每一个隐藏层可以写成以下的非线性函数：

其中输入层 H⁽⁰⁾ = X , 输出层 H^(L) = Z , L 是层数。 不同的GCN模型，采用不同 f (· ，·) 函数。

2.2 模型定义

论文中采用的函数如下

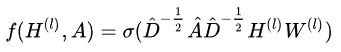
首先物理上它起的作用是，每一个节点下一层的信息是由前一层本身的信息以及相邻的节点的信息加权加和得到，然后再经过线性变换以及非线性变换。
对于上面那个复杂的公式，可以先采用最简单的层级传导（ layer-wise propagation ）规则

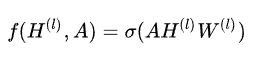
我们直接将 AH 做矩阵相乘，然后再通过一个权重矩阵 W 做线性变换，之后再经过非线性激活函数 , 比如说 ReLU，最后得到下一层的输入 H^(l+1) 。

最为关键的AH的意思，通过下面的演示可以得到解释,假设每个节点 X_i = [i ,i ,i ,i ] , 采用的是上面给出的图结构, 那么在经过矩阵相乘之后

A = torch.tensor([
    [0,1,0,0,1,0],
    [1,0,1,0,1,0],
    [0,1,0,1,0,0],
    [0,0,1,0,1,1],
    [1,1,0,1,0,0],
    [0,0,0,1,0,0]
])

H_0 = torch.tensor([
    [1,1,1,1],
    [2,2,2,2],
    [3,3,3,3],
    [4,4,4,4],
    [5,5,5,5],
    [6,6,6,6]
])

A.matmul(H_0)
>>>tensor([[ 7,  7,  7,  7],
        [ 9,  9,  9,  9],
        [ 6,  6,  6,  6],
        [14, 14, 14, 14],
        [ 7,  7,  7,  7],
        [ 4,  4,  4,  4]])

所以我们知道 AH 就是把通过邻接矩阵，快速将相邻的节点的信息相加得到自己下一层的输入，但是仅仅通过这种操作，会带来两类问题

1. 虽然获得了周围节点的信息了，但是自己本身的信息却没了（除非自己有一条边指向自己）
2. 从上面的结果也可以看出，在经过一次的 AH 矩阵变换后，得到的输出会变大，即特征向量 X 的scale会改变，在经过多层的变化之后，将和输入的scale差距越来越大。

采用的解决方案是，对每个节点手动增加一条self-loop 到每一个节点，即

其中 I 是单位矩阵。

考虑将邻接矩阵 A 做归一化使得最后的每一行的加和为1，使得 AH 获得的是weighted sum。
将 A 的每一行除以行的和，这就可以得到normalized的 A 。而其中每一行的和，就是每个节点的度degree。用矩阵表示则为： A = D^-1 A , 对于 A_ij = A_ij / d_ij

A = torch.tensor([
      [0,1,0,0,1,0],
      [1,0,1,0,1,0],
      [0,1,0,1,0,0],
      [0,0,1,0,1,1],
      [1,1,0,1,0,0],
      [0,0,0,1,0,0]
  ], dtype=torch.float32)
  
  D = torch.tensor([
      [2,0,0,0,0,0],
      [0,3,0,0,0,0],
      [0,0,2,0,0,0],
      [0,0,0,3,0,0],
      [0,0,0,0,3,0],
      [0,0,0,0,0,1],
  ], dtype=torch.float32)
  
  hat_A = D.inverse().matmul(A)
  
  >>>hat_A
  tensor([[0.0000, 0.5000, 0.0000, 0.0000, 0.5000, 0.0000],
          [0.3333, 0.0000, 0.3333, 0.0000, 0.3333, 0.0000],
          [0.0000, 0.5000, 0.0000, 0.5000, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.3333, 0.0000, 0.3333, 0.3333],
          [0.3333, 0.3333, 0.0000, 0.3333, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000]])

在实际运用中我们采用的是对称的normalization:

A内部采取的操作就是：

将以上结合起来，就可以得到