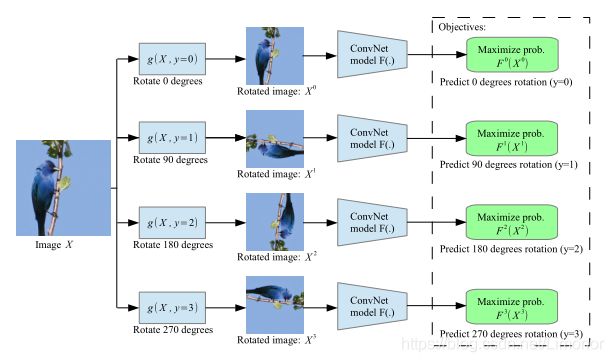
自监督学习--图像上色论文 Colorful Image Colorization

这是一篇比较老的论文了，是加里福利亚大学Richard Zhang发表在ECCV 2016上的文章，论文的工作是灰度图的自动着色，但是是属于自监督学习pretext task的一篇代表任务工作，而且论文的效果确实比较好，贴一个后面的web应用

点击这里Demo，可以自己拿照片试一试

这是这篇论文的展示页面，东西很全

论文github地址：https://github.com/richzhang/colorization

一、自监督介绍

有监督 无监督 自监督 的区别

见这篇

一句话总结，传统的深度学习需要大量的人工标注数据，自监督学习通过pretext task（前置任务）学习数据内部分布，生成伪标签来训练模型，打破了标签数据的局限，更接近人工智能的本质。

自监督学习一般有三大常见的前置任务，分别是

图像旋转

图像拼图（图像补全）

图像上色

其实他们都是预测任务，比如预测图像旋转的角度，预测图像分块后每一块的相对位置，还有这篇文章的预测图像的颜色，本质是学习图像的语义特征。

为什么这么说，就是站在人类认知的角度，我们为什么看到一张参天大树的图像，可以判断它是直立的？因为我们知道天空和地面的上下位置关系，树的常见状态我们也知道，所以我们能不假思索地判断出来。预测图片拼图和上色也是一样，我们学习到了图像的语义特征信息。而自监督学习可以不需要人为的标签标注，也是充分学习了图像的内部数据的结果。

二、论文导读

三、idea分析

论文目的：给灰度图像上色

创新点：由于图像的颜色具有多模态性质，即一张图像的颜色可以有多种可能，因此文章不是重建图像颜色，而是预测图像颜色。

（用灰度图中物体的纹理、语义等信息作为线索，来预测可能的上色，最后的上色结果只要真实即可。这不仅降低了上色的难度，而且也符合人们的认知）

idea：颜色预测是一个多模的问题，一个物体本来就可以上不同的颜色。对这种多模性建模，为各个像素预测一个颜色的分布，这可以鼓励探索颜色的多样性，而不仅仅局限在某一种颜色中。

前向encoder+ 反向decoder+ab概率分布预测的网络结构

前人工作：前人的目标只是优化预测结果和真实图片（ground truth）间的欧氏距离（即MSE）（L2范式），这种损失函数会把所有的颜色求平均（因为颜色具有多模态），从而导致颜色饱和度不高，色彩不丰富。

本文的思路可概括为3点：设计损失函数 + 加权平滑像素损失 + 概率分布转点估计。

四、Lab颜色空间

文章的上色思路就是：我们有三个颜色通道$L$ $a$ $b$，输入 $L$ 通道，模型来预测 $ab$ 的通道。通过 $ab$ 通道的概率值，转化为 $ab$ 的色道值，最终达到上色的效果，是一种量化颜色空间的方式。

关于lab颜色通道，它是颜色空间的其中一种。颜色空间一般有：RGB空间、CIE XYZ颜色空间、Lab颜色空间以及HSV颜色空间等等。

Lab颜色空间：

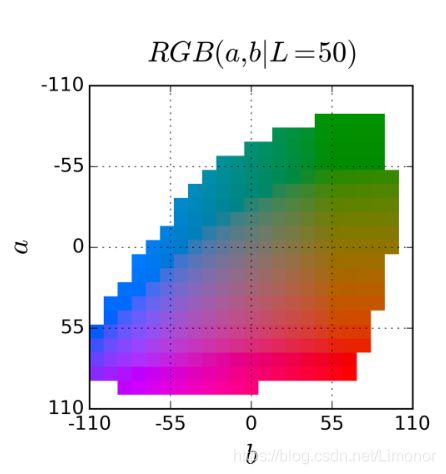
Lab颜色模型基于人对颜色的感觉，其数值描述正常视力的人能够看到的所有颜色。因为 Lab描述的是颜色的显示方式，而不是设备（如显示器、桌面打印机或数码相机）生成颜色所需的特定色料的数量，所以Lab被视为与设备无关的颜色模型。Lab色彩模型是由亮度（L）和有关色彩的a、b三个要素组成，L表示亮度，a表示从洋红色至绿色的范围，b表示从黄色至蓝色的范围。L的值域由0到100，L=50时，就相当于50%的黑色；a和b的值域都是由+127至-128，其中当a=+127时颜色为红色，当a渐渐过渡到-128时变成绿色；同样原理，当b=+127是黄色，b=-128是蓝色，所有的颜色就以这三个值交互变化所组成，其空间如图所示。

五、模型结构

一共8层卷积，每层卷积块由许多小conv2d块和relu组成，5和6两层用到了空洞卷积。

基本模型还是比较简单的，输入图片的 $L$ 通道，使用一个CNN预测对应的 $ab$ 通道取值的概率分布，最后转化为RGB图像结果。

整个模型$\mathcal{F}$最终包含两个部分：用于预测所有像素颜色分布的卷积神经网络$\mathcal{G}$，和用于产生最终预测图像的退火平均操作$\mathcal{H}$。虽然整个系统不能严格意义的端到端训练，但是可以注意到$\mathcal{H}$是对每个像素单独作用的，只有一个参数，可以作为CNN的前向转播的一部分实现。

六、量化，权重，解码

传统的损失函数：给定输入的 $L$ 通道$X\in {\mathbb{R}}^{H\times W\times 1}$，现在的目标是学习一个到相应 $ab$ 通道$Y\in {\mathbb{R}}^{H\times W\times 2}$的映射$\hat{Y}=\mathcal{F}(X)$，使用预测结果和真实图像间的 $L_2$ 损失：
$$L_2(\hat{Y},Y)=\frac{1}{2}\sum _{h,w}{\Vert Y_{h,w}-{\hat{Y}}_{h,w}\Vert }_2^2$$

但是这种方法有明显的局限，问题在于图像的上色没有一个确定的最优解，真值也只是提供了一种参考。而且直接使用L2损失函数得到的结果精度不会很高，很有可能会得到一个ab通道的均值。即如果一个物体可以上若干种颜色，L2 损失函数的最优解将会是这几种颜色的平均值，直观上来看就是那些灰色的，不饱和的结果。

因此，作者在这里将图像上色转换为了一个分类问题，而且使用软编码的方式保证上色的多样性，使用类别均衡化保证颜色的丰富度，具体的步骤如下：

1.量化

对颜色空间进行量化。因为要预测的是两个波段，所以直接分类是不可行的，因此需要对预测空间进行编码。作者在这里采用的是一个比较直接的编码方式，直接将ab波段以10为间隔进行划分，划分成313个类别。下面的图表示了量化的结果

将待量化的a，b与每个区间的中心a，b计算距离，然后对这些距离的平方做类似softmax的处理变成概率，作者称之为soft-encoding，encoding结果作为该a，b的量化结果。

Soft-encoding的代码：

wts = np.exp(-dists**2/(2 * sigma**2))
wts = wts / np.sum(wts)

其中dists是当前a，b与每个区间的中心a，b计算的距离，sigma是方差，论文中取5。

作者使用 $Z$ 表示量化的标签，既然对颜色空间做了量化，那么其实就可以利用类似查表的方法得到标签，但是作者在这里使用了软编码的方式设置标签，可以使得上色的选择更加多样。所谓软编码方法是指图像中某个位置 $(h,w)$ 的不是由这一位置的 $ab$ 通道值$Y$单独确定，而是选取周围5个相邻的值，并且根据他们距离 $Y$ 的距离进行高斯加权。

最终的损失函数为：
$${\mathrm{L}}_{cl}(\mathrm{Z},\mathbf{Z})=-\sum _{h,w}v\left({\mathbf{Z}}_{h,w}\right)\sum _q{\mathbf{Z}}_{h,w,q}\log \left({\mathbf{Z}}_{h,w,q}\right)$$

2.权重

作者在1300万张图片数据上统计发现，低饱和度的颜色数量非常大，如果忽视这种情况，训练的模型的输出依然是低饱和的图片。因此需要通过权重来使得类尽可能的均衡。

权重的计算方法是：统计训练图片a，b量化后的分布（只取距离最近的），对分布使用高斯函数进行平滑，平滑后的分布的倒数即可作为权重。这里作者在加权重和不加权重上做了个折中，可以理解为最后的损失有2部分，一部分是没有乘权重的，另一部分是乘了权重的。论文通过在计算的权重上加一个均匀分布来实现这种折中。

本文使用了一种加权平滑像素损失的方式，在训练的时候为每个像素的loss重新调整权重，这个权重的大小是基于像素颜色的稀有度来设置的，通过统计ImageNet训练集的色彩概率分布，我们可以获取色素的稀有程度，使用类似于代价敏感的方法，对于越稀有的色素给予更大的权重和关注力，从而实现平滑的效果。

3.解码

模型对于每个位置输出313个可能颜色的概率，用所得的概率对313个区间的中心加权求和可得到最终的颜色。论文中通过实验发现，如果直接用模型输出的概率计算颜色，颜色饱和度会比较低；如果只选取最大的概率的区间所表示的颜色，整个图片会不连续。作者通过下面这个公式来调整模型输出的概率，然后用改变后的概率对区间中心加权求和得到最终的颜色：

$$\frac{\exp (\log (\mathbf{z})/T)}{{\sum }_q\exp \left(\log \left({\mathbf{z}}_q\right)/T\right)}$$

在将ab色道概率分布转换成ab色道值时，可以有两种方式，一种是直接取每个色素概率最大的值作为预测值，对应T=0,颜色较为鲜艳，但会出现色彩不连续，另一种是取预测分布的平均值，对应T=1,无色彩不连续现象，但是色彩较为不饱和，因此这里使用一种比较持重的、模拟退火的算法找到一个偏向最优的平衡点T=0.38。

七、代码

这篇论文虽然是四年前的，但是很幸运，作者在上个月更新了代码，将原来的caffe框架换成了pytorch，并添加了一种新的模型。

论文主要的模型eccv16，代码如下，主要是对网络模型结构的一个搭建，可以对比模型结构图查看

eccv16.py

class ECCVGenerator(BaseColor):
    def __init__(self, norm_layer=nn.BatchNorm2d):
        super(ECCVGenerator, self).__init__()
		
		# 定义网络结构，一共有8层conv网络层
		# 每一层conv都有二维卷积块和relu块，最后以BatchNorm layer结束
        model1=[nn.Conv2d(1, 64, kernel_size=3, stride=1, padding=1, bias=True),]
        model1+=[nn.ReLU(True),]
        model1+=[nn.Conv2d(64, 64, kernel_size=3, stride=2, padding=1, bias=True),]
        model1+=[nn.ReLU(True),]
        model1+=[norm_layer(64),]

        model2=[nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1, bias=True),]
        model2+=[nn.ReLU(True),]
        model2+=[nn.Conv2d(128, 128, kernel_size=3, stride=2, padding=1, bias=True),]
        model2+=[nn.ReLU(True),]
        model2+=[norm_layer(128),]

        model3=[nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1, bias=True),]
        model3+=[nn.ReLU(True),]
        model3+=[nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1, bias=True),]
        model3+=[nn.ReLU(True),]
        model3+=[nn.Conv2d(256, 256, kernel_size=3, stride=2, padding=1, bias=True),]
        model3+=[nn.ReLU(True),]
        model3+=[norm_layer(256),]

        model4=[nn.Conv2d(256, 512, kernel_size=3, stride=1, padding=1, bias=True),]
        model4+=[nn.ReLU(True),]
        model4+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
        model4+=[nn.ReLU(True),]
        model4+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
        model4+=[nn.ReLU(True),]
        model4+=[norm_layer(512),]

		# 第5层和第6层dilation=2，采用了空洞卷积
        model5=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
        model5+=[nn.ReLU(True),]
        model5+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
        model5+=[nn.ReLU(True),]
        model5+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
        model5+=[nn.ReLU(True),]
        model5+=[norm_layer(512),]

        model6=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
        model6+=[nn.ReLU(True),]
        model6+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
        model6+=[nn.ReLU(True),]
        model6+=[nn.Conv2d(512, 512, kernel_size=3, dilation=2, stride=1, padding=2, bias=True),]
        model6+=[nn.ReLU(True),]
        model6+=[norm_layer(512),]

        model7=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
        model7+=[nn.ReLU(True),]
        model7+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
        model7+=[nn.ReLU(True),]
        model7+=[nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1, bias=True),]
        model7+=[nn.ReLU(True),]
        model7+=[norm_layer(512),]

        model8=[nn.ConvTranspose2d(512, 256, kernel_size=4, stride=2, padding=1, bias=True),]
        model8+=[nn.ReLU(True),]
        model8+=[nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1, bias=True),]
        model8+=[nn.ReLU(True),]
        model8+=[nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1, bias=True),]
        model8+=[nn.ReLU(True),]

		# 最后一层对应到图中红色的方块区域，256到313的量化分布
        model8+=[nn.Conv2d(256, 313, kernel_size=1, stride=1, padding=0, bias=True),]

        self.model1 = nn.Sequential(*model1)
        self.model2 = nn.Sequential(*model2)
        self.model3 = nn.Sequential(*model3)
        self.model4 = nn.Sequential(*model4)
        self.model5 = nn.Sequential(*model5)
        self.model6 = nn.Sequential(*model6)
        self.model7 = nn.Sequential(*model7)
        self.model8 = nn.Sequential(*model8)

        self.softmax = nn.Softmax(dim=1)
        # 输出层，将313的输入通道转为2的输出通道，返回ab的通道
        self.model_out = nn.Conv2d(313, 2, kernel_size=1, padding=0, dilation=1, stride=1, bias=False)
        # 上采样层，线性4倍空间大小上采样
        # （论文原话）分辨率的所有更改都是通过转换块之间的空间下采样或上采样实现的
        self.upsample4 = nn.Upsample(scale_factor=4, mode='bilinear')

	# 前向传递搭建网络层，输入input_l（输入的灰度图像L通道）
    def forward(self, input_l):
        # 输入的L通道经过归一化后输入CONV1层
        conv1_2 = self.model1(self.normalize_l(input_l))
        conv2_2 = self.model2(conv1_2)
        conv3_3 = self.model3(conv2_2)
        conv4_3 = self.model4(conv3_3)
        conv5_3 = self.model5(conv4_3)
        conv6_3 = self.model6(conv5_3)
        conv7_3 = self.model7(conv6_3)
        conv8_3 = self.model8(conv7_3)
        # ECCVGenerator的输出结果是第8层CONV的softmax的输出层计算结果 
        # 返回的（应该是）ab的通道预测概率 
        out_reg = self.model_out(self.softmax(conv8_3))
		# 返回的是ab颜色的值
        return self.unnormalize_ab(self.upsample4(out_reg))

针对 L a b 的颜色空间做的一些数值处理

base_color.py

import torch
from torch import nn

class BaseColor(nn.Module):
	def __init__(self):
		super(BaseColor, self).__init__()

		self.l_cent = 50.
		self.l_norm = 100.
		self.ab_norm = 110.

	# 给L通道做归一化处理
	def normalize_l(self, in_l):
		return (in_l-self.l_cent)/self.l_norm

	def unnormalize_l(self, in_l):
		return in_l*self.l_norm + self.l_cent

	def normalize_ab(self, in_ab):
		return in_ab/self.ab_norm

	def unnormalize_ab(self, in_ab):
		return in_ab*self.ab_norm

跑代码

我是在colab上运行的，按照README的提示，很容易可以跑通

克隆项目

!git clone https://github.com/richzhang/colorization.git

进入到目录中后，安装依赖项

!pip install requirements.txt

运行demo_release.py这个程序，测试imgs文件夹里面的图片

!python demo_release.py -i imgs/我的图片

展示几张图片的效果

基本发现一些规律，对于自然场景的照片或者相机拍摄的图像，预测的效果很好；但是面对绘制的图像或者动漫图片，模型的学习能力就很差了。可能是训练的时候使用的大部分数据集都是自然图像，

总结

本文主要对图像的上色问题进行了研究，将图像的上色问题转化为分类问题，通过颜色空间的量化和类别的均衡，保证了上色结果的多样性。另外，作者还验证了其作为自监督方法的性能，在Pascal VOC 的分类检测和分割任务上均取得了不错的成绩。

在自监督学习任务中，随机丢弃图像的颜色或者让网络对图像进行部分上色是非常有帮助的，无论我们的自监督模型有没有显式地图像上色任务，我们都可以在数据増广阶段随机将图像转化为灰度图或其他色域的图像。