详解3D物体检测模型: Voxel Transformer for 3D Object Detection
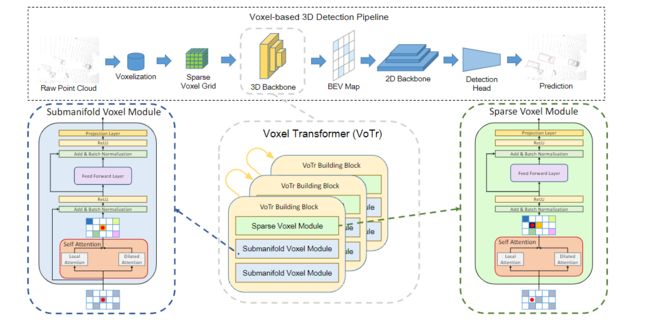
本文介绍一个新的的3D物体检测模型:VoTr,论文已收录于ICCV 2021。 这是第一篇使用 voxel-based Transformer 做3D 主干网络,用于点云数据3D物体检测。由于有限的感受野,传统的 3D 卷积网络检测器(voxel-based)不能有效地捕获大量的环境信息, 于是在本文中作者引入基于 Transformer 的结构,通过自注意力的方式寻找长距离范围内 voxel 之间的关系。
本文主要贡献有:
- 考虑到非空
voxel的稀疏性及数量众多的事实,直接对voxel使用标准的Transformer并不是一件容易的事情。为此,作者提出了sparse voxel module和submanifold voxel module,它们可以有效地对空的和非空的voxel进行操作。 - 为了进一步增大注意力范围,同时维持与卷积检测器相对应的计算开销,作者进一步提出了两种
多头注意力机制:Local Attention和Dilated Attention,同时作者还进一步提出了Fast Voxel Query,用于加速voxel的查询。 - 本文提出的
VoTr方法可以用在大多数voxel-based的3D检测器,最后作者在Waymo和KITTI数据集上进行了实验,证明本文提出的方法在提高检测性能时并且保持了相当的计算效率。
论文链接为:https://arxiv.org/pdf/2109.02497.pdf
项目链接为:https://github.com/PointsCoder/VOTR
文章目录
-
-
- 1. Introduction & Related Work
- 2. Voxel Transformer
-
- 2.1 Overall Architecture
- 2.2 Voxel Transformer Module
- 2.3 Efficient Attention Mechanism
- 2.4 Fast Voxel Query
- 3. Experiments
-
1. Introduction & Related Work
首先是论文引言部分。之前的 3D 检测方法主要分别两种:point-based 和 voxel-based,voxel-based 的方法首先对点云做栅格化处理,将点云转化为一个个 voxel 然后使用 3D 卷积网络提取特征。之后将 voxel 转换为鸟瞰图最终在鸟瞰图上生成 3D boxes。
但是由于感受野受限,影响着检测器性能。例如,SECOND 模型 voxel 大小是 ( 0.05 m , 0.05 m , 0.1 m ) (0.05m,0.05m,0.1m) (0.05m,0.05m,0.1m),最后一层最大的感受野是 ( 3.65 m , 3.65 m , 7.3 m ) (3.65m,3.65m,7.3m) (3.65m,3.65m,7.3m),覆盖不了一辆长度为 4 m 4m 4m 的汽车。感受野的大小与 voxel size V V V,kernel size K K K,downsample stride S S S,layer number L L L 四者乘积成正比。增大 V V V 会导致点云量化误差变大;增大 K K K 会导致卷积特征成三次方增大;增大 S S S 会导致低精度的鸟瞰图,会降低最终预测结果; 增大 L L L 会需要更多的计算资源。但是在3D物体检测时,由于点云的稀疏性和不完整性,而我们又需要增大感受野,因此就需要设计一种新的架构来编码更多的上下文信息。
最近 Transformer 在2D物体分类、检测、分割任务上取得了不错的效果,主要是因为自注意力机制可以建立像素间的长距离关系。但是直接将 Transformer 用到 voxel 中会遇到两个问题:
- 非空的
voxel分布很稀疏,而图像中像素是很密集的,例如在Waymo数据集中非空的voxel只占所有的voxel0.1 % 0.1\% 0.1%,因此需要设计一个特殊操作只作用于那些非空的voxel上; - 非空
voxel的数量是庞大的,例如在Waymo数据集中达到了 90 k 90k 90k,如果像标准的Transformer那样使用全连接自注意力在计算上是吃不消的,因此,非常需要新的方法来扩大注意力范围,同时将每个 query 的注意力 voxel 数保持在较小的范围内。
为了解决这两个问题,作者于是提出了 VoTr,具体方法在下一节介绍。下图是3D卷积网络和 VoTr 的感受野图示。在图(a)中,橘色立方体表示的是3D卷积核,黄色的 voxel 被以红色 voxel 为中心的最大感受野所包含。在图(b)中,红色的 voxel 是待查询的 voxel,蓝色 voxel 是它的注意力 voxel,作者发现只使用一个自注意力层就可以覆盖比整个卷积骨干网还要大的区域,而且还可以保持足够细微的3D结构。
- 点云3D物体检测方法:
Frustum-PointNet、PointRCNN、3DSSD、VoxelNet、SECOND、HVNet、PV-RCNN; Transformer在计算机视觉的应用:ViT、DETR、SETR、MaX-DeepLab、Point Transformer、Pointformer;
2. Voxel Transformer
2.1 Overall Architecture
现在我们来开始详细介绍 VoTr。整体结构设计和 SECOND 很相似,VoTr 包含三个 sparse voxel module,降采样3次,每一个 sparse voxel module 跟着2个 submanifold voxel module,在所有的模块中都使用到了多头注意力机制。在多头注意力机制中,每一个 query voxel 使用了两种特别的注意力方法:Local Attention 、 Dilated Attention。
值得注意的是:submanifold voxel module 只在非空的 voxel 进行注意力操作,而 sparse voxel module 可以在空的 voxel 上提取特征。
2.2 Voxel Transformer Module
- self-attention on sparse voxels
这里首先介绍 sparse voxel 上的自注意力方法。
- 假设总共有 N d e n s e N_{dense} Ndense 个
voxels,非空voxel索引数组 V : N s p a r s e × 3 \mathcal{V}:N_{sparse} \times 3 V:Nsparse×3 以及对应特征数组 F : N s p a r s e × d \mathcal{F}:N_{sparse} \times d F:Nsparse×d,且 N sparse ≪ N dense N_{\text {sparse }} \ll N_{\text {dense }} Nsparse ≪Ndense 。 - 特定地,一个要查询的
voxeli i i,其注意力范围 Ω ( i ) ⊆ V \Omega(i) \subseteq \mathcal{V} Ω(i)⊆V 是由注意力机制确定,对注意力voxelj ⊆ Ω ( i ) j \subseteq \Omega(i) j⊆Ω(i) 进行多头注意力操作,得到注意力特征 f i a t t e n d f^{attend}_{i} fiattend。 - 令 f i , f j ∈ F f_i,f_j\in\mathcal{F} fi,fj∈F 分别为查询和注意力
voxel特征, v i , v j ∈ V v_i,v_j\in\mathcal{V} vi,vj∈V 分别为查询和注意力voxel整数索引。根据索引得到voxel中心坐标 p i , p j p_i,p_j pi,pj,其中 p = t × ( v + 0.5 ) p=t\times(v+0.5) p=t×(v+0.5)。然后可以计算 Q i , K i , V i Q_i,K_i,V_i Qi,Ki,Vi:
Q i = f i W q , K j = f j W k + E pos , V j = f j W v + E p o s (1) Q_{i}=f_{i} W_{q}, K_{j}=f_{j} W_{k}+E_{\text {pos }}, V_{j}=f_{j} W_{v}+E_{p o s} \tag{1} Qi=fiWq,Kj=fjWk+Epos ,Vj=fjWv+Epos(1)位置编码 E p o s E_{pos} Epos 为:
E p o s = ( p i − p j ) W p o s (2) E_{p o s}=\left(p_{i}-p_{j}\right) W_{p o s} \tag{2} Epos=(pi−pj)Wpos(2)自注意力特征为:
f i a t t e n d = ∑ j ∈ Ω ( i ) σ ( Q i K j d ) ⋅ V j (3) f_{i}^{a t t e n d}=\sum_{j \in \Omega(i)} \sigma\left(\frac{Q_{i} K_{j}}{\sqrt{d}}\right) \cdot V_{j} \tag{3} fiattend=j∈Ω(i)∑σ(dQiKj)⋅Vj(3)
其中, σ ( ⋅ ) \sigma(\cdot) σ(⋅) 是softmax归一化函数,这里可以将 3Dvoxel的自注意力机制看作是 2D 的自注意力机制的扩展,使用的相对坐标作为位置编码。
- submanifold voxel module
此模块,包含两层网络,第一层是自注意层,连接所有的注意力机制,第二层是简单的前向传播层,这里也使用了残差连接。与标准的 Transformer 不同的是:
- 在前向传播层之后添加了线性投影层用于调整特征通道数量;
- 使用了
BN替代LN; - 删除了
dropout,这是因为这里的注意力voxel数量太少了,再使用dropout可能会阻碍学习过程;
- sparse voxel module
由于在非空 voxel 没有特征,于是得不到 Q i Q_i Qi,使用如下方法得到近似 Q i Q_i Qi:
Q i = A j ∈ Ω ( i ) ( f j ) (4) Q_{i}=\underset{j \in \Omega(i)}{\mathcal{A}}\left(f_{j}\right) \tag{4} Qi=j∈Ω(i)A(fj)(4)其中 A \mathcal{A} A 是对所有注意力 voxel 特征做最大池化操作,同样地使用公式(3) 进行多头注意力操作,这里没有使用残差连接。
2.3 Efficient Attention Mechanism
现在,着重介绍注意力范围 Ω ( i ) \Omega(i) Ω(i),注意力机制中非常重要的一个因素。 Ω ( i ) \Omega(i) Ω(i) 应当满足以下三点:
- Ω ( i ) \Omega(i) Ω(i) 应该能覆盖相邻的
voxel以保持细微的3D结构; - Ω ( i ) \Omega(i) Ω(i) 覆盖的范围应尽可能的远以便获得更大的上下文信息;
- Ω ( i ) \Omega(i) Ω(i) 所包含的
voxel数应该尽可能的少,例如小于50,避免计算负载过大;
- local attention
定义 ∅ ( s t a r t , e n d , s t r i d e ) \varnothing(start,end,stride) ∅(start,end,stride) 为一个返回非空索引的函数,例如 ∅ ( ( 0 , 0 , 0 , ) , ( 1 , 1 , 1 ) , ( 1 , 1 , 1 ) ) \varnothing((0,0,0,),(1,1,1),(1,1,1)) ∅((0,0,0,),(1,1,1),(1,1,1)) 返回为 ∅ { ( 0 , 0 , 0 , ) , ( 0 , 0 , 1 ) , ( 0 , 1 , 0 ) , . . . , ( 1 , 1 , 1 ) } \varnothing\{(0,0,0,),(0,0,1),(0,1,0),...,(1,1,1)\} ∅{(0,0,0,),(0,0,1),(0,1,0),...,(1,1,1)} 八个非空索引。在 Local Attention 中,注意力范围为:
Ω local ( i ) = ∅ ( v i − R local , v i + R local , ( 1 , 1 , 1 ) ) (5) \Omega_{\text {local }}(i)=\varnothing\left(v_{i}-R_{\text {local }}, v_{i}+R_{\text {local }},(1,1,1)\right) \tag{5} Ωlocal (i)=∅(vi−Rlocal ,vi+Rlocal ,(1,1,1))(5) 其中 R local = ( 1 , 1 , 1 ) R_{\text{local}}=(1,1,1) Rlocal=(1,1,1),注意的是这里只返回非空 voxel 的索引。
- dilated attention
注意力范围为:
Ω dilated ( i ) = ⋃ m = 1 M ∅ ( v i − R end ( m ) , v i + R end ( m ) , R stride ( m ) ) \ ∅ ( v i − R start ( m ) , v i + R start ( m ) , R stride ( m ) ) , (6) \begin{array}{r} \Omega_{\text {dilated }}(i)=\bigcup_{m=1}^{M} \varnothing\left(v_{i}-R_{\text {end }}^{(m)}, v_{i}+R_{\text {end }}^{(m)}, R_{\text {stride }}^{(m)}\right) \backslash \\ \varnothing\left(v_{i}-R_{\text {start }}^{(m)}, v_{i}+R_{\text {start }}^{(m)}, R_{\text {stride }}^{(m)}\right), \end{array} \tag{6} Ωdilated (i)=⋃m=1M∅(vi−Rend (m),vi+Rend (m),Rstride (m))\∅(vi−Rstart (m),vi+Rstart (m),Rstride (m)),(6)
其中 \ \backslash \ 是集合相减运算符, R start ( i ) < R end ( i ) ≤ R start ( i + 1 ) , R stride ( i ) < R stride ( i + 1 ) R_{\text {start }}^{(i)}
。经过认真设计,注意力机制所能搜寻的范围可以达到15m,而查询的 voxel 数量可以小于50。
下图是一个2D的注意力机制说明(可以轻松扩展到3D场景)。对于要查询的 voxel (红色所示),Local Attention 关注的是局部区域,浅蓝色 voxel 在查询范围内,最终被选择为注意力 voxel;Dilated Attention 查询的范围比较大(绿色所示),最终非空的 voxel 被选择为注意力 voxel。

2.4 Fast Voxel Query
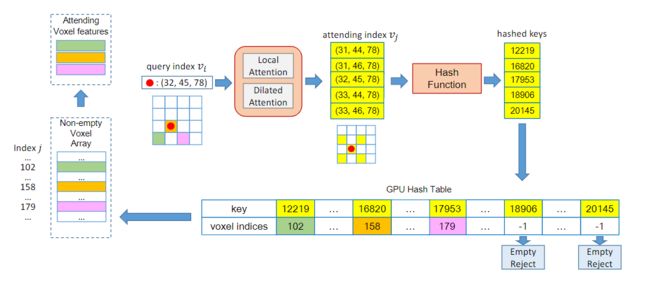
在上面设计的注意力机制中,查询每个非空的注意力 voxel 是至关重要的。为了查询每个注意力 voxel 可能要花费 O ( N sparse ) O\left(N_{\text {sparse }}\right) O(Nsparse ) 时间复杂度,这是十分耗时的(Waymo 数据集中 N sparse = 90 k N_{\text{sparse}} = 90k Nsparse=90k),因此作者在这里提出了一个基于哈希表的快速查询。
快速查询流程如下图所示,这里与之前的查询方法不同的是,在哈希表中只需要查询 N Ω N_{\Omega} NΩ 次, Ω \Omega Ω 是注意力范围, N Ω ≪ N sparse N_{\Omega} \ll N_{\text {sparse }} NΩ≪Nsparse 。
3. Experiments
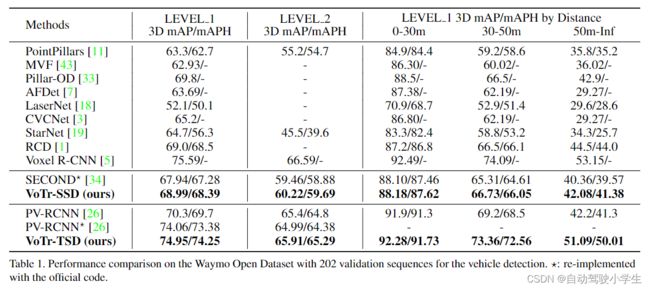
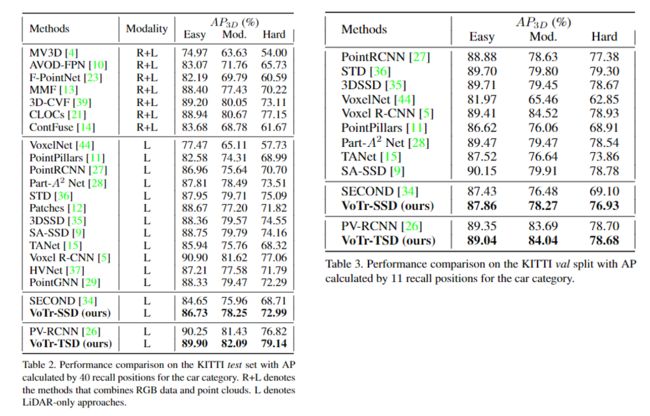
下面是实验部分,作者分别在 Waymo 和 KITTI 数据上进行了测试。VoTr-SSD 选择 SECOND 作为检测框架,VoTr-TSD 选择 PV-RCNN 作为检测框架,将传统的3D卷积替换为本文设计的 Transformer 结构。下面是 Waymo 验证集上的结果。
下面是在 KITTI 数据集上的结果。这里在 SECOND 框架上提升比较多。
最后是消融实验,可以看到不同注意力机制、dropout 参数、注意力 voxel 数量、模型参数、推理速度以及注意力权重的比较。