高等数学学习笔记(1)——微分方程解法公式
本文列举了微分方程的公式,当做一个笔记,如果后面有地方用得上就回来翻翻。
当然本文是为了求解模型中用得上的微分方程而书写的,并非是为了考研或者本科课程应试,所以不会有例题,只会有对应的解法。同时公式和解法不一定是完全的,后面如果还遇到了到时候再进行补充。
对了宝贝儿们,卑微小李的公众号【野指针小李】已开通,期待与你一起探讨学术哟~摸摸大!
目录
- 1 微分方程
- 2 一阶方程
-
- 2.1 一阶线性微分方程
- 2.2 变量可分离
- 2.3 齐次方程
- 2.4 伯努利方程
- 2.5 全微分方程
- 3 高阶方程
-
- 3.1 可降解方程
-
- 3.1.1 y ′ ′ = f ( x , y ′ ) y''=f(x,y') y′′=f(x,y′)
- 3.1.2 y ′ ′ = f ( y , y ′ ) y''=f(y,y') y′′=f(y,y′)
- 3.2 高阶常系数微分方程
-
- 3.2.1 都是单根
- 3.2.2 有重根
- 3.2.3 有复数根
- 4 参考
1 微分方程
要了解微分方程,得从微分说起,微分的核心是变化率。就比如速度 v = d x d t v=\frac{dx}{dt} v=dtdx,即每一时刻距离的变化;而加速度 a = d v d t a=\frac{dv}{dt} a=dtdv,即每一时刻速度的变化。
有了这个概念后,我们再来看微分方程,简单来说就是由变化率构成的一个方程。其使用场景为:描述相对变量比绝对量更容易时。
微分方程分为两部分:
- 常微分方程(Ordinary Differential Equations, ODE):函数自变量只有一个,如: y ′ ( x ) = p y + q y'(x)=py+q y′(x)=py+q。
- 偏微分方程(Partial Differential Equations, PDE):函数有多个自变量,如: ∂ T ∂ t ( x , y , t ) = ∂ 2 T ∂ x 2 ( x , y , t ) + ∂ 2 T ∂ y 2 ( x , y , t ) \frac{\partial T}{\partial t}(x,y,t)=\frac{\partial^2T}{\partial x^2}(x,y,t)+\frac{\partial^2T}{\partial y^2}(x,y,t) ∂t∂T(x,y,t)=∂x2∂2T(x,y,t)+∂y2∂2T(x,y,t)
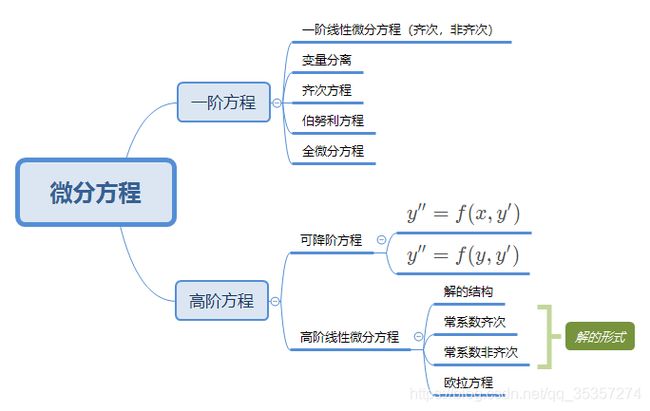
微分方程也可以分为一阶方程和高阶方程,具体的组成(解法)如下图:
2 一阶方程
2.1 一阶线性微分方程
形如:
y ′ + p ( x ) y = q ( x ) y'+p(x)y=q(x) y′+p(x)y=q(x)
若:
- q ( x ) = 0 q(x)=0 q(x)=0,则是一阶线性齐次微分方程;
- q ( x ) ≠ 0 q(x)≠0 q(x)=0,则是一阶线性非齐次微分方程;
通解:
y = e − ∫ p ( x ) d x [ ∫ q ( x ) e ∫ p ( x ) d x d x + c ] y=e^{-\int p(x)dx}[\int q(x)e^{\int p(x)dx}dx+c] y=e−∫p(x)dx[∫q(x)e∫p(x)dxdx+c]
2.2 变量可分离
形如:
∫ g ( y ) d y = ∫ f ( x ) d x \int g(y)dy=\int f(x)dx ∫g(y)dy=∫f(x)dx
解法:
d y d x = g ( y ) f ( x ) → G ( y ) = F ( x ) + c \frac{dy}{dx}=\frac{g(y)}{f(x)} \rightarrow G(y)=F(x)+c dxdy=f(x)g(y)→G(y)=F(x)+c
就是将 d y dy dy与 d x dx dx移到一边,其余的移动到另外一边。
2.3 齐次方程
形如:
d y d x = f ( y x ) \frac{dy}{dx}=f(\frac{y}{x}) dxdy=f(xy)
解法:
- 令 y x = u \frac{y}{x}=u xy=u,则 d y = u d x + x d u dy=udx+xdu dy=udx+xdu
- 代入原方程。
2.4 伯努利方程
形如:
y ′ + p ( x ) y = q ( x ) y n y'+p(x)y=q(x)y^n y′+p(x)y=q(x)yn
解法:
- 等式两边同时除 y n y^n yn,得到 y − n y ′ + y 1 − n p ( x ) = q ( x ) y^{-n}y'+y^{1-n}p(x)=q(x) y−ny′+y1−np(x)=q(x)
- 令 y 1 − n = u y^{1-n}=u y1−n=u;
- 对第二步结果求导得: ( 1 − n ) y − n y ′ = d u d x → y − n y ′ = u ′ 1 − n = 1 1 − n d u d x (1-n)y^{-n}y'=\frac{du}{dx} \rightarrow y^{-n}y'=\frac{u'}{1-n}=\frac{1}{1-n}\frac{du}{dx} (1−n)y−ny′=dxdu→y−ny′=1−nu′=1−n1dxdu;
- 将步骤3结果与步骤2结果代入步骤1: 1 1 − n d u d x + u p ( x ) = q ( x ) \frac{1}{1-n} \frac{du}{dx}+up(x)=q(x) 1−n1dxdu+up(x)=q(x);
- 接着依据步骤4的情况来选择使用什么通解公式求解。
2.5 全微分方程
形如:
P ( x , y ) d x + Q ( x , y ) d y = 0 P(x,y)dx+Q(x,y)dy=0 P(x,y)dx+Q(x,y)dy=0
就是说函数 P P P和函数 Q Q Q都是包含了 x x x和 y y y的。
解法:
- 线积分法: Φ ( x , y ) = ∫ x 0 x P ( x , y ) d x + ∫ y 0 y Q ( x , y ) d y \Phi(x,y)=\int_{x_0}^x P(x,y)dx+\int_{y_0}^y Q(x,y)dy Φ(x,y)=∫x0xP(x,y)dx+∫y0yQ(x,y)dy或 Φ ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P ( x , y ) d x + Q ( x , y ) d y \Phi(x,y)=\int_{(x_0,y_0)}^{(x,y)} P(x,y)dx+Q(x,y)dy Φ(x,y)=∫(x0,y0)(x,y)P(x,y)dx+Q(x,y)dy
- 偏积分法: ∂ Φ ∂ x = P ( x , y ) , ∂ Φ ∂ y = Q ( x , y ) \frac{\partial \Phi}{\partial x}=P(x,y), \frac{\partial \Phi}{\partial y}=Q(x,y) ∂x∂Φ=P(x,y),∂y∂Φ=Q(x,y),第一个等式对 x x x积分得 Φ ( x , y ) = ∫ P ( x , y ) d x + ψ ( y ) \Phi (x,y)=\int P(x,y)dx+\psi (y) Φ(x,y)=∫P(x,y)dx+ψ(y),代入第二个等式求 ψ ( y ) \psi(y) ψ(y),即可得 Φ ( x , y ) \Phi(x,y) Φ(x,y)
- 凑微分法:凑微分得 Φ ( x , y ) \Phi(x,y) Φ(x,y)
3 高阶方程
3.1 可降解方程
3.1.1 y ′ ′ = f ( x , y ′ ) y''=f(x,y') y′′=f(x,y′)
解法:
- 令 y ′ = P ( x ) y'=P(x) y′=P(x),则 y ′ ′ = P ′ ( x ) y''=P'(x) y′′=P′(x)
- 代入原方程: P ′ ( x ) = f ( x , P ( x ) ) P'(x)=f(x,P(x)) P′(x)=f(x,P(x)),求 P ( x ) P(x) P(x)
- 将 P ( x ) P(x) P(x)积分求得通解
3.1.2 y ′ ′ = f ( y , y ′ ) y''=f(y,y') y′′=f(y,y′)
解法:
- 令 y ′ = P ( y ) y'=P(y) y′=P(y), y ′ ′ = d P d y d y d x = P d P d y y''=\frac{dP}{dy} \frac{dy}{dx}=P\frac{dP}{dy} y′′=dydPdxdy=PdydP
- 代入原方程得: P d P d y = f ( y , P ( y ) ) P\frac{dP}{dy}=f(y,P(y)) PdydP=f(y,P(y))
- 求解 P ( y ) P(y) P(y)得 d y d x \frac{dy}{dx} dxdy
- 对 P ( y ) P(y) P(y)积分求得通解
3.2 高阶常系数微分方程
定义:
a n d n y d x n + a n − 1 d n − 1 y d x n − 1 + . . . + a 1 d y d x + a 0 y = f ( x ) a_n \frac{d^ny}{dx^n} + a_{n-1} \frac{d^{n-1}y}{dx^{n-1}} + ... + a_1 \frac{dy}{dx}+a_0y=f(x) andxndny+an−1dxn−1dn−1y+...+a1dxdy+a0y=f(x)
若:
- f ( x ) = 0 f(x)=0 f(x)=0,则为齐次方程;
- f ( x ) ≠ 0 f(x)≠0 f(x)=0,则为非齐次方程。
由于我现在还用不上高阶常系数非齐次微分方程,所以没有看特解的求法,如果以后看了在做补充。
高阶常系数齐次微分方程解的结构为:
y = c 1 y 1 ( x ) + c 2 y 2 ( x ) + . . . + c n y n ( x ) y=c_1y_1(x)+c_2y_2(x)+...+c_ny_n(x) y=c1y1(x)+c2y2(x)+...+cnyn(x)
齐次方程的解法为:
- 先将非齐转换为齐,即令 f ( x ) = 0 f(x)=0 f(x)=0
- 找到特征方程的特征根,假设微分方程为 y ′ ′ + 2 y ′ + y = 0 y''+2y'+y=0 y′′+2y′+y=0,特征方程为 λ 2 + 2 λ + 1 = 0 \lambda^2+2\lambda+1=0 λ2+2λ+1=0,其特征根: λ 1 = λ 2 = − 1 \lambda_1=\lambda_2=-1 λ1=λ2=−1,即 λ \lambda λ最高为多少次,那么就有多少个特征根
- 通过特征根形式来寻找通解公式。
现在问题转换为了特征根形式,特征根从大方向上来说一共有3类:
- 每个特征根都是单重根;
- 有重根;
- 有复数根。
3.2.1 都是单根
通解为:
y = c 1 e λ 1 x + c 2 e λ 2 x + . . . + c n e λ n x y=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}+...+c_ne^{\lambda_nx} y=c1eλ1x+c2eλ2x+...+cneλnx
3.2.2 有重根
通解为:
y = c 1 e λ x + c 2 x e λ x + . . . + c n x n − 1 e λ x = e λ x ( c 1 + c 2 x + . . . + c n x n − 1 ) y=c_1e^{\lambda x}+c_2xe^{\lambda x}+...+c_nx^{n-1}e^{\lambda x}=e^{\lambda x}(c_1+c_2x+...+c_nx^{n-1}) y=c1eλx+c2xeλx+...+cnxn−1eλx=eλx(c1+c2x+...+cnxn−1)
3.2.3 有复数根
λ = α ± i β \lambda = \alpha \pm i\beta λ=α±iβ,这里虽然复数是成对出现,但是当做是一个根。
先给出通解形式,再补充点推导过程。
通解:
y = c 1 e α x c o s β x + c 2 e α x s i n β x y=c_1e^{\alpha x}cos\beta x+c_2e^{\alpha x}sin\beta x y=c1eαxcosβx+c2eαxsinβx
推导过程:
先补充欧拉方程:
e i x = c o s x + i s i n x e^{ix}=cosx+isinx eix=cosx+isinx
由欧拉公式进行推导,先推导 λ = α + i β \lambda = \alpha + i\beta λ=α+iβ:
e ( α + i β ) x = e α x + i β x = e α x ( c o s β x + i s i n β x ) = e α x c o s β x + i e α x s i n β x = c 1 e α x c o s β x + c 2 e α x s i n β x \begin{aligned} e^{(\alpha + i\beta)x} &= e^{\alpha x + i \beta x} \\ & = e^{\alpha x}(cos\beta x + isin\beta x) \\ & = e^{\alpha x}cos\beta x + i e^{\alpha x}sin\beta x \\ & = c_1e^{\alpha x}cos\beta x+c_2e^{\alpha x}sin\beta x \end{aligned} e(α+iβ)x=eαx+iβx=eαx(cosβx+isinβx)=eαxcosβx+ieαxsinβx=c1eαxcosβx+c2eαxsinβx
这里 c 2 c_2 c2实际上是包含了 i i i的。
同理, λ = α − i β \lambda = \alpha - i\beta λ=α−iβ如下:
e ( α − i β ) x = e α x − i β x = e α x ( c o s β x − i s i n β x ) = e α x c o s β x − i e α x s i n β x = c 1 e α x c o s β x + c 2 e α x s i n β x \begin{aligned} e^{(\alpha - i\beta)x} &= e^{\alpha x - i \beta x} \\ & = e^{\alpha x}(cos\beta x - isin\beta x) \\ & = e^{\alpha x}cos\beta x - i e^{\alpha x}sin\beta x \\ & = c_1e^{\alpha x}cos\beta x+c_2e^{\alpha x}sin\beta x \end{aligned} e(α−iβ)x=eαx−iβx=eαx(cosβx−isinβx)=eαxcosβx−ieαxsinβx=c1eαxcosβx+c2eαxsinβx
因为 c o s ( − x ) = c o s x , s i n ( − x ) = − s i n x cos{(-x)}=cosx,sin(-x)=-sinx cos(−x)=cosx,sin(−x)=−sinx,所以可以获得上面公式,这里 c 2 c_2 c2是包含了 − i -i −i的。
4 参考
[1]3Blue1Brown.【官方双语】微分方程概论-第一章[EB/OL].https://www.bilibili.com/video/BV1tb411G72z,2019-4-24.
[2]3Blue1Brown.【官方双语】微分方程概论-第二章:什么是偏微分方程?[EB/OL].https://www.bilibili.com/video/BV1q4411p7NX,2019-5-27.
[3]math也是柠檬精.半小时内搞定一阶常微分方程(带技巧和例题)[EB/OL].https://www.bilibili.com/video/BV1qJ411A7QK?from=search&seid=10597070231979640473,2019-9-15.
[4]math也是柠檬精.半小时搞定高阶线性微分方程[EB/OL].https://www.bilibili.com/video/BV1qE411h7yp,2019-10-29.
[5]柠檬草嘉6的店.可降解的高阶微分方程[EB/OL].https://wenku.baidu.com/view/c05bb71cdcccda38376baf1ffc4ffe473368fda4.html,2019-3-8.
[6]风车飞了的店.全微分方程的解法[EB/OL].https://wenku.baidu.com/view/faefc09dc4da50e2524de518964bcf84b8d52d6c.html,2018-11-16.