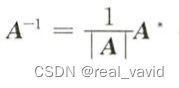线代——求逆矩阵的快捷方法
1、二阶矩阵
A = [ a b c d ] A = \begin{bmatrix} a & b\\ c & d \end{bmatrix} A=[acbd],其逆矩阵 A − 1 = 1 a d − b c [ d − b − c a ] A^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix} A−1=ad−bc1[d−c−ba]
2、分块矩阵
分块矩阵在主对角位置,直接对分块矩阵取逆矩阵:
A = [ X Y ] A = \begin{bmatrix} X & \\ & Y \end{bmatrix} A=[XY],其逆矩阵 A − 1 = [ X − 1 Y − 1 ] A^{-1}=\begin{bmatrix} X^{-1} & \\ & Y^{-1} \end{bmatrix} A−1=[X−1Y−1]
分块矩阵在副对角位置,副对调,再取逆:
A = [ X Y ] A = \begin{bmatrix} & X \\ Y & \end{bmatrix} A=[YX],其逆矩阵 A − 1 = [ Y − 1 X − 1 ] A^{-1}=\begin{bmatrix} & Y^{-1}\\ X^{-1} & \end{bmatrix} A−1=[X−1Y−1]
分块矩阵为右上三角形状,首先主对角直接取逆,然后再对右上角子矩阵左乘其行,右乘其列,再添符号:
A = [ X W Y ] A = \begin{bmatrix} X & W\\ & Y \end{bmatrix} A=[XWY],其逆矩阵 A − 1 = [ X − 1 − X − 1 W Y − 1 Y − 1 ] A^{-1}=\begin{bmatrix} X^{-1} & -X^{-1}WY^{-1}\\ & Y^{-1} \end{bmatrix} A−1=[X−1−X−1WY−1Y−1]
同理,对于左下三角形状,首先主对角直接取逆,然后再对左下角子矩阵左乘其行,右乘其列,再添符号:
A = [ X W Y ] A = \begin{bmatrix} X & \\ W & Y \end{bmatrix} A=[XWY],其逆矩阵 A − 1 = [ X − 1 − Y − 1 W X − 1 Y − 1 ] A^{-1}=\begin{bmatrix} X^{-1} & \\ -Y^{-1}WX^{-1} & Y^{-1} \end{bmatrix} A−1=[X−1−Y−1WX−1Y−1]
它们相同之处,都是分块三角矩阵占据主对角位置。
分块矩阵为左上三角形状,首先副对调,再取逆,然后将左上角子矩阵换到右下角,最后再对该子矩阵左乘其行,右乘其列,再添符号:
A = [ W X Y ] A = \begin{bmatrix} W & X \\ Y & \end{bmatrix} A=[WYX],其逆矩阵 A − 1 = [ Y − 1 X − 1 − X − 1 W Y − 1 ] A^{-1}=\begin{bmatrix} & Y^{-1}\\ X^{-1} & -X^{-1}WY^{-1} \end{bmatrix} A−1=[X−1Y−1−X−1WY−1]
同理,对于右下三角形状,首先副对调,再取逆,然后将右下角子矩阵换到左上角,最后再对该子矩阵左乘其行,右乘其列,再添符号:
A = [ X Y W ] A = \begin{bmatrix} & X \\ Y & W \end{bmatrix} A=[YXW],其逆矩阵 A − 1 = [ − Y − 1 W X − 1 Y − 1 X − 1 ] A^{-1}=\begin{bmatrix} -Y^{-1}WX^{-1} & Y^{-1}\\ X^{-1} & \end{bmatrix} A−1=[−Y−1WX−1X−1Y−1]
它们相同之处,都是分块三角矩阵占据副对角位置。
综上,对于形状是上、下三角的分块矩阵求逆,如果分块子矩阵占据主对角位置,不需要对调位置;如果分块子矩阵占据副对角位置,都需要对调位置。