CNN中2d卷积算子的分析与实验

CNN中2d卷积算子的分析与实验

为了和之前的GNN中图卷积算子的实验相对应，本次实验主要对CNN中的2d卷积进行了分析。

在CNN中，我们通过卷积的计算操作来提取图像局部的特征，每一层都会计算出一些局部特征，这些局部特征再汇总到下一层，这样一层一层的传递下去，特征由小变大，最后在通过这些局部的特征对图片进行处理，这样大大提高了计算效率，也提高了准确度。

2d卷积作为一种基本的算子，广泛应用于很多模型当中，例如LeNet、AlexNet、GoogleNet、ResNet。和GNN不同，各种不同CNN模型的卷积操作都是一致的，即（在pytorch中）都是用函数torch.nn.Conv2d为基础来构建整个模型（只不过卷积的参数略有区别），具体模型结构可以。因此，使用何种模型进行实验反而不那么重要了。

经典的模型结构可以参考：https://github.com/zergtant/pytorch-handbook/blob/master/chapter2/2.4-cnn.ipynb

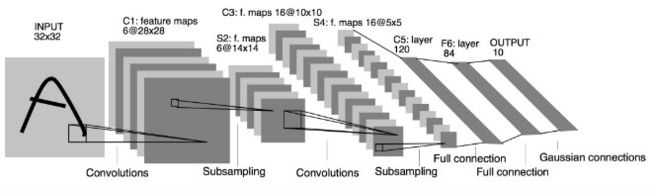
下面的实验是在手写数字识别实验的基础上进行的——用LeNet-5来训练MNIST数据集。

torch.nn.Conv2d的研究与分析

torch.nn.Conv2d的源代码在torch/nn/modules/conv.py中实现，而通过查看源代码又可以将核心的2d卷积操作追溯到F.conv2d()函数，但找不到这个对应的 python 代码，只是在文件torch/_C/_VariableFunctions.pyi中进行了函数的声明，因为它来自于通过C++编写的THNN库（为了加速）。

追溯的路径和思路如下：

torch.nn.Conv2d-->torch/nn/modules/conv.py-->F.conv2d()-->torch/_C/_VariableFunctions.pyi-->C++编写的THNN库

总之，得出的结论是，在pytorch中，2d卷积的核心代码是用C++写的！

由于pytorch对这些C++编写的库提前进行了编译和链接，然后进行了封装，所以直接去修改这些需要去改动整个pytorch框架，难度和工程量都是相当庞大的。

因此，下面的实验选择根据2d卷积的原理重写了conv2d的python代码，并在划分阶段后加入了计时机制。

• 缺点：程序的运行速度显著减慢。
  • 使用自带的F.conv2d()执行5个epoch的总时间：61.9329s
  • 使用自己重写_conv2d并加入计时机制后执行5个epoch的总时间：880.9045s
  • 运行速度慢了大约14倍。
• 优点：便于程序的修改和实验。

重写conv2d的思路以及阶段的划分

首先要搞清楚torch.nn.Conv2d都在干些什么。

class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)

宏观上，输入数据的维度为[batch_size, in_channel, h_in, w_in ]，通过2d卷积层后的输出维度为[batch_size, out_channel, h_out, w_out]。可以发现，除了第一维batch_size，后面的三个维度（通道数，图片的高，图片的宽）都会发生变化。

• 输入数据的维度为[batch_size, in_channel, h_in, w_in ]
• 卷积层权重的维度为[out_channel, in_channel // group(默认为1), kernel_size, kernel_size]
• 2d卷积层后的输出维度为[batch_size, out_channel, h_out, w_out]

那么微观上一个单位的2d卷积操作是究竟是如何进行的呢？

1. 切片输入数据[batch_size, in_channel, h_in, w_in ]–>[batch_size, in_channel, kernel_size, kernel_size ]
2. 切片得到的数据和卷积层的权重进行多维点积操作：先进行广播操作（None的那一维），再进行点积。
   [batch_size, None, in_channel, kernel_size, kernel_size ] * [None, out_channel, in_channel, kernel_size, kernel_size]–>[batch_size, out_channel, in_channel, kernel_size, kernel_size ]
3. 将点积得到数据的最后三维进行求和[batch_size, out_channel, in_channel, kernel_size, kernel_size ]–>[batch_size, out_channel]

上面是一个单位的2d卷积操作的过程，对所有的像素进行滑动（循环上述过程），则最终可以得到卷积后的结果了[batch_size, out_channel, h_out, w_out]。

例如，在实验中的一个单位的2d卷积操作过程中，输入数据的维度变化是这样的：

[64,1,28,28]-->切片-->[64,1,5,5]-->点积[64,1,1,5,5]*[1,6,1,5,5]=[64,6,1,5,5]-->求和-->[64,6]-->循环后-->[64,6,24,24]

根据上面的思路，可以将卷积操作划分为三个基本阶段，每个阶段所做的操作就是上面的3个步骤：

1. 切片Slice。核心的运算是张量Tensor的切片操作。
2. 点积Dot。核心的运算是张量之前的点积操作。
3. 求和Sum。核心的运算是张量后三维的求和操作。

实验

在实验中，我对每个epoch中这三个阶段的平均时间进行了统计。

参考：https://github.com/Jintao-Huang/dnn_study/blob/master/torch_%E5%BA%95%E5%B1%82%E7%AE%97%E6%B3%95%E5%AE%9E%E7%8E%B0/only_forward.py

我的代码：https://github.com/ytchx1999/CNN-Test

• 实验环境：云服务器 + 一块Tesla T4 + PyTorch。
  • CPU
    型号：Intel® Xeon® Gold 5218 CPU
    内存：128G
    内核：64核
  • GPU
    Tesla T4 *1
    显存：16G
• 数据集：MNIST。
• 计时单位：s。

这次的计时单位是秒。

conv2d中的各阶段执行时间

各阶段的执行时间/s	Slice	Dot	Sum
LeNet	0.4597	19.2618	27.4245

第一次执行的是使用自带的函数，第二次执行使用的是重写后的函数。这5个epoch的训练结果相似，也证明了重写的conv2d函数的有效性（除了速度有点慢）。