CS224W 4 Graph as Matrix: PageRank,Random Walks and Embeddings
目录
Link Analysis approaches—计算图中节点重要性
PageRank—"Flow" Model
基本思路
随机邻接矩阵M
M和Random Walk联系起来
M和eigenvector centrality的联系
Summary
power iteration—计算PageRank
problems—dead ends&Spider traps和随机跳动
pagerank 优点
PageRank solution Summary
Personalized PageRank&Random Walks with Restarts
3、PageRank、Personalized PageRank、Random Walks with Restarts的区别
Matrix Factorization and Node Embeddings
Summary
本课从矩阵的视角对图进行分析。将图视为矩阵：
- 通过random walk决定节点重要性(PageRank)
- 通过矩阵分解获得node embedding(MF)
- 将node embeddings(例如，Node2Vec)视为MF
可以发现random walk、MF、node embeddings是相关的
Link Analysis approaches—计算图中节点重要性
以网页为例，节点是web pages 边是超链接，仅考虑早期导航类型的超链接，不考虑现在事务性的超链接(发布评论、购买)。web是有向边。
web pages的重要性并不相同，利用web graph的链接结构为pages的重要性排序。
- 如果pages有更多in-coming links，则page更重要—仅计数
- 来自更重要的page的链接更加重要，我的邻居重要我也重要—递归问题
PageRank—"Flow" Model
基本思路
一个页面很重要：如果他被其他重要的pages指向。
- 每个链接的投票与其源页面的重要性成正比
- 如果具有重要性的页面 i 具有 di 个连出链接，则每个链接都会获得 ri / di 投票
- 页面j本身的重要性rj是其连入链接的投票总和
rj 是节点j的importance score
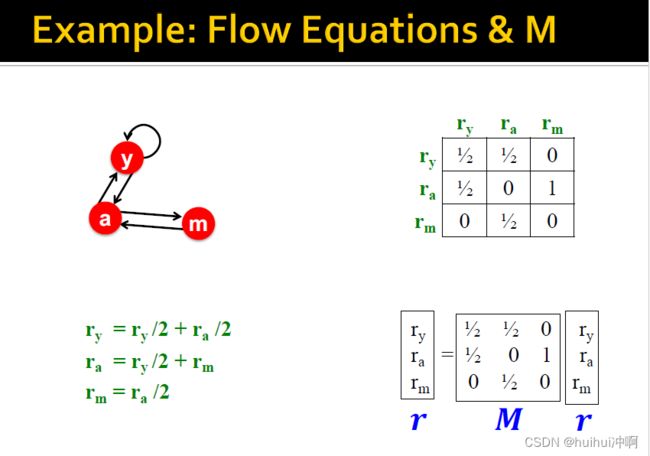
随机邻接矩阵M
利用M计算上述的Flow equation(如果利用Gaussian elimination则太复杂)
M的限制条件 :M的每列和要为1。
flow equation可以写为：r = M*r
M和Random Walk联系起来
r是random walk的一个稳定分布(经过多次迭代)
M和eigenvector centrality的联系
rank vector(重要性得分)r 是随机邻接矩阵M特征值为1的特征向量
Summary
PageRank:
- 使用 Web 的链接结构测量图中节点的重要性
- 使用随即邻接矩阵M模拟 random web surfer
- PageRank 的解r = Mr 其中r可以看做M的特征值为0的特征向量或者图上random walk的稳定分布
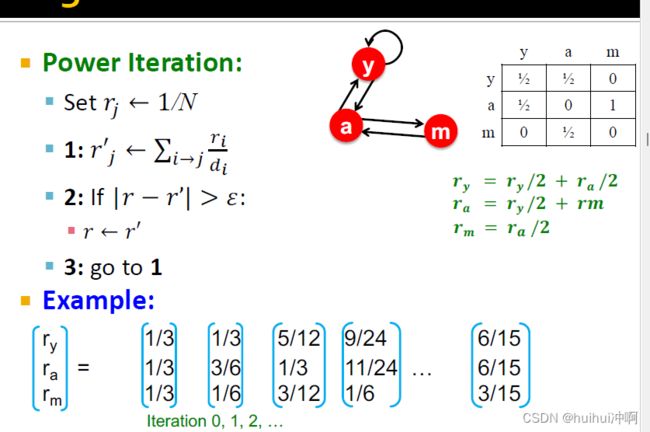
power iteration—计算PageRank
problems—dead ends&Spider traps和随机跳动
spider traps:所有重要性被一个page吸收，其他的为0
重要性泄露出去了，所有page imporatance都变为0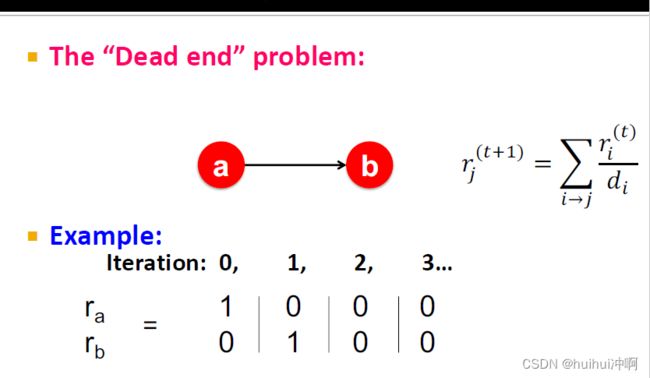
Spider Traps:每次random suffer有两个选择：以概率β遵循任意一个链接，或者以1-β的概率，跳到任意一个页面
dead —每次都随机跳到任意一个page
Google's solution
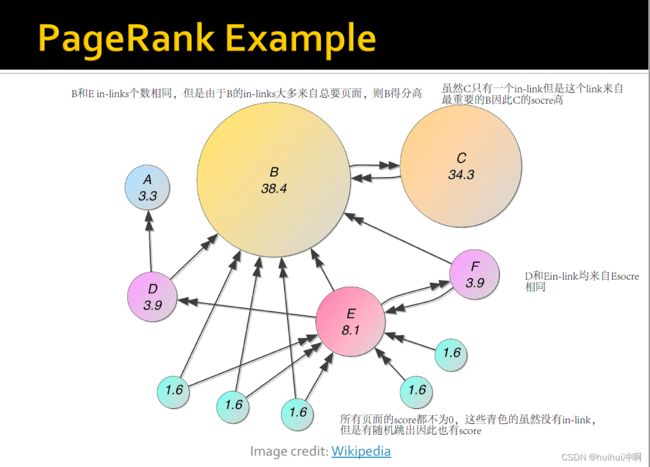
pagerank 优点
可以使所有pages的重要性score都不为0
PageRank solution Summary
使用power iteration求解
使用跳出解决dead-ends与 spider-traps
Personalized PageRank&Random Walks with Restarts
以给定一个二部图代表用户和item互动(购买)为例。
1、目标：图上的临近性
- 应该向和商品Q互动发用户推荐什么商品？
- 直觉：如果Q和P被相似的用户互动，那么当用户购买Q时，应该推荐P
2、节点临近性度量。
3、PageRank、Personalized PageRank、Random Walks with Restarts的区别
在传送时：PageRank以相同概率传到任意一个节点； Personalized PageRank可以以不同概率传到一个节点子集中节点； Random Walks with Restarts每次传送都跳到初始节点Q
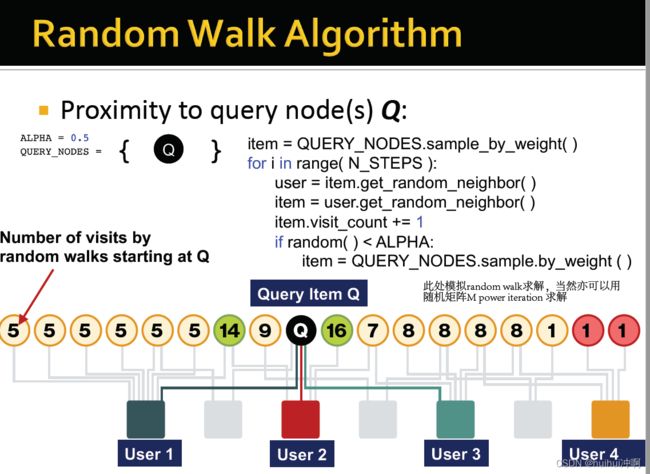
4、 Random Walks with Restarts步骤
以node Q为例：
不断迭代—找到Q的任意一个user；直到user的任一个item；访问的对应item次数加一；以一定概率返回Q。
最后item出现次数最多的为最重要
此处模拟random walk求解，当然亦可以用随机矩阵M power iteration 求解
Matrix Factorization and Node Embeddings
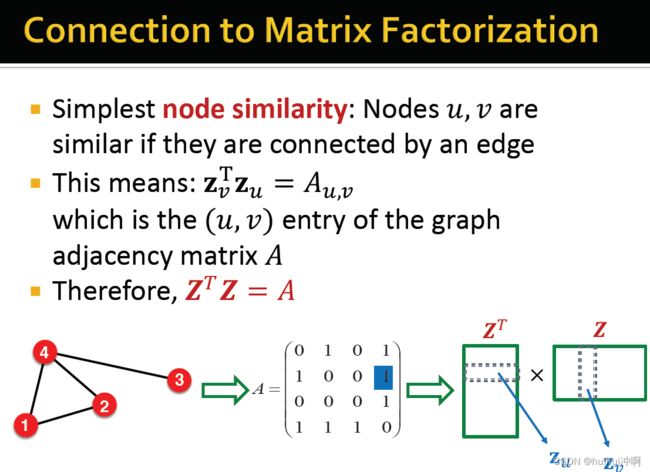
1、以最简单的节点相似性为例：如果节点u和v相连，那么他们相似，可以把节点嵌入的内积当作邻接矩阵。
具有由边连通性定义的节点相似性的内积解码器等效于 邻接矩阵A 的矩阵分解
2、DeepWalk embedding的矩阵分解更加复杂
3、node embeddings 通过 matrix factorization and random walks的限制
- 不能获得不在训练集里的节点的embedding，如果增加新节点的话需要重新计算所有节点的embedding
- 不能捕获结构相似性，例如节点1和11虽然局部结构相似，但从Random Walk无法从节点1走到11 因此两者会有非常不同的embedding。
- 不能利用节点、边、或图的feature属性信息
这些限制可以利用深度Representation和图神经网络解决
Summary
